(a) State Ampere's circuital law, expressing it in the integral form.
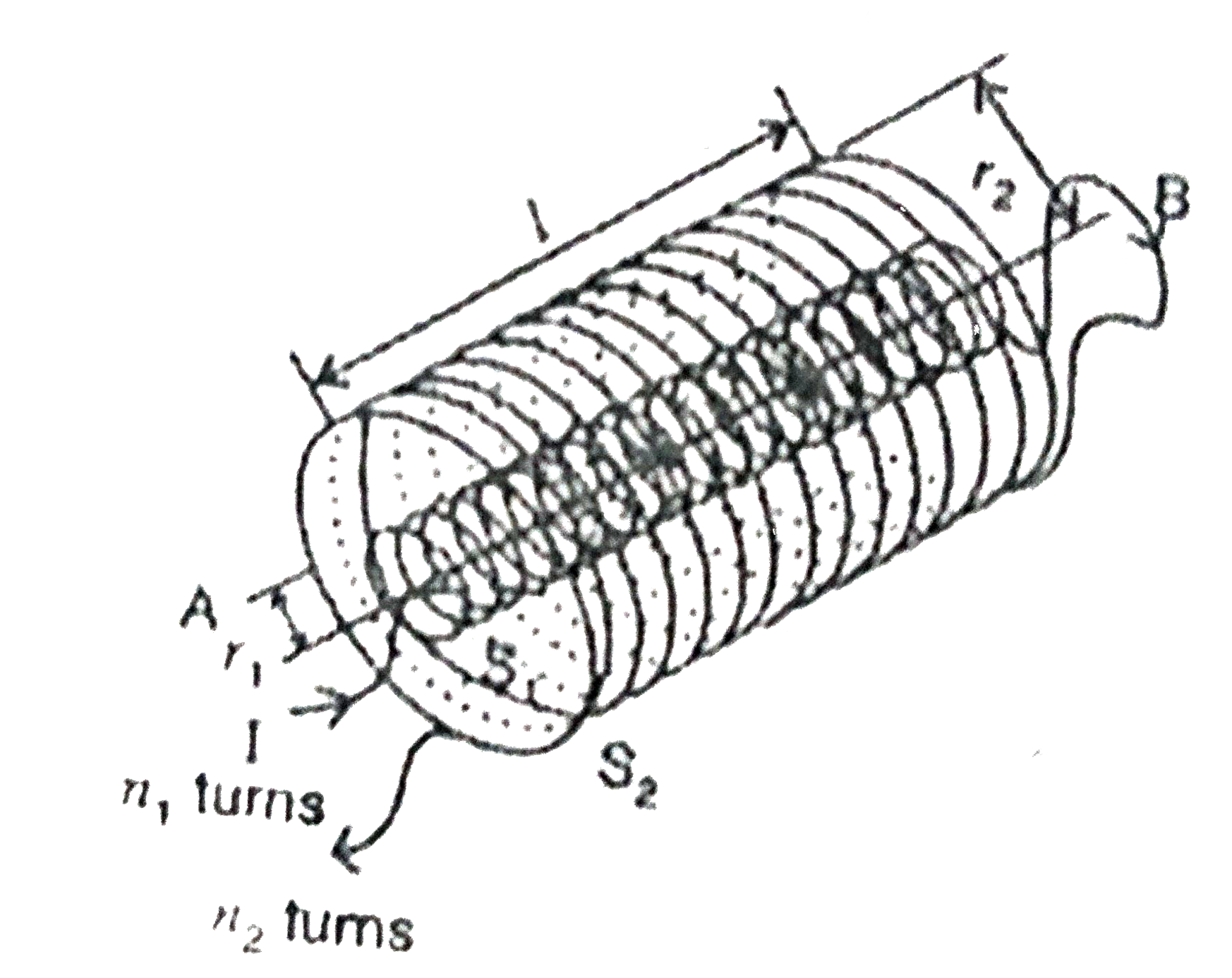
(b) Two long coaxial inlsulated soenoids, S1 and S2 of equal lengths are would one over the other as shown in the figure. A steady current ''I'' flows through the inner solenoid S1 to the other end B, which is connected to the outer solenoid S2 through which the same current ''I'' flows in the opposite direction so as the come out at end A. If n1 and n2 are the number of turns per unit length, find the magnitude and direction of the net magnetic field at a point
(i) inside on the axis and
(ii) outside the combined system.
(a) Ampere's circuital law states that the circulation of the resultant magnetic field along a closed plane curve is equal to time the total current crossing the area bounded by the closed curve, provided the electric field inside the loop remains constant.
In the above illustration, the Ampere's circuital law can be written as follow :
(b) (i) The magnetic field due to a current carrying solenoid :
where, N = number of turns per unit length i = current through the solenoid Now, the magnetic field due to solenoid S1 will be in the upward direction and the magnetic field due to S2 will be in the downward direction (by right-hand screw rule).
In the upward direction.
(ii) The magnetic field is zero outside a solenoid.
Topper's Solved these Questions
- XII BOARDSBook:XII BOARD PREVIOUS YEAR PAPER ENGLISHChapter:XII BOARDSExercise:[SET - II DELHI BOARD]
Explore 5 Videos
- XII BOARDSBook:XII BOARD PREVIOUS YEAR PAPER ENGLISHChapter:XII BOARDSExercise:[SET - III, DELHI BOARD]
Explore 6 Videos
- XII BOARDSBook:XII BOARD PREVIOUS YEAR PAPER ENGLISHChapter:XII BOARDSExercise:SET-II
Explore 33 Videos
- SAMPLE PAPER 2019Book:XII BOARD PREVIOUS YEAR PAPER ENGLISHChapter:SAMPLE PAPER 2019Exercise:SECTION D
Explore 6 Videos
Similar Questions
State Ampere's circuital law, expressing it in integral form.
View Solution(a) State Ampère's circuital law expressing it in the integral form.
(b) Two long coaxial insulated solenoids S1 and S2 of equal lengths are wound one over the other as shown in the figure. A steady current 'I' flows through the inner solenoid S1 , to the other end B which is connected to the outer solenoid S2 , through which the same current 'I' flows in the opposite direction so as to come out at end A. If n1 , and n2 are the number of turns per unit length, find the magnitude and direction of the net magnetic field at a point (i) inside on the axis and (ii) outside the combined system.
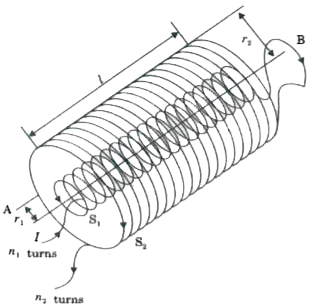
View Solution
Knowledge Check
A solenoid is connected to a battery so that a steady current flows through it. If an iron core is inserted into the solenoid, then
AThe current will not changeBThe current will increaseCthe current will decreaseDthe flux through the coil will decrease.A solenoid is connected to a battery so that a steady current flows through it. If an iron core is inserted into the solenoid, then
AincreaseBdecreaseCremains sameDfirst increase then decreaseAn infinite long solenoid having n turns per unit length is shown in figure. The magnetic field at P, when a current I is flowing through it would be
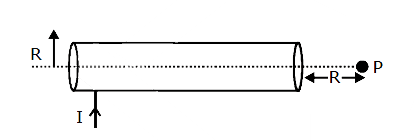 Aμ0nIBzeroCμ0nI2√2Dμ0nI2[1−1√2]
Aμ0nIBzeroCμ0nI2√2Dμ0nI2[1−1√2]
Two long coaxical insulated solenoid's S1 and S2 of equal lengths are would one over the other as shown in figure. A steady current 'T' flows through the inner solenoid S1 to the other end B, which is connected to the outer solenoid S2 through which the same current flows in opposite direction so as to come out at end A. If n1 and n2 are the number of turns per unit length, find the magnitude and direction of net magnetic field at a point (i) inside on the axis and (ii) outside the combined system.
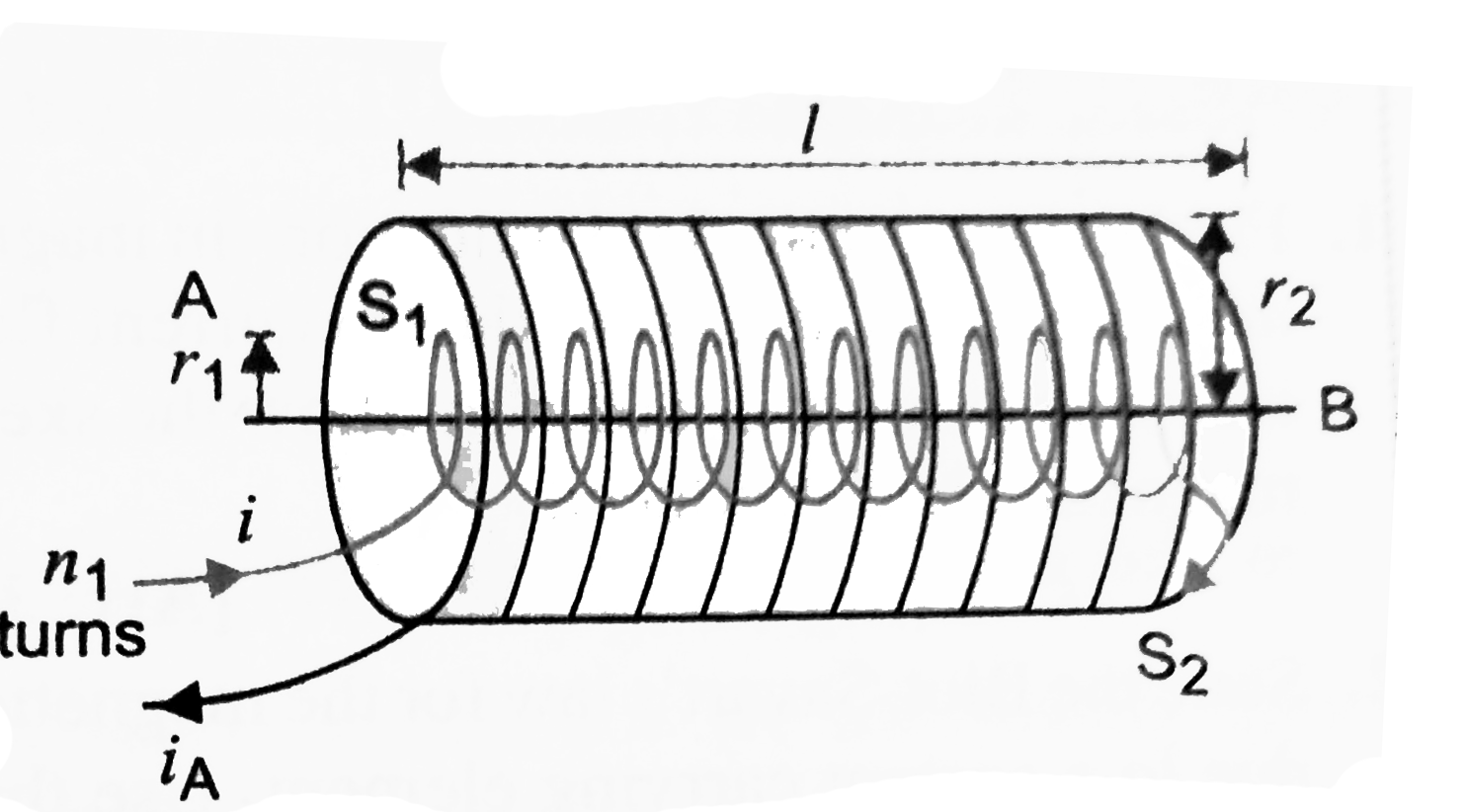
View SolutionTwo long coaxial insulated solenoids, S1andS2 of equal lengths are wound one over the other as shown in the figure. A steady current "I" flow through the inner solenoid S1 to the other end B, which is connected to the outer solenoid S2 through which the same current "I" flows inthe opposite direction so as to come out at end A. If n1 and n2 are the number of turns per unit length, find the magnitude and direction of the net magnetic field at a point (i) inside on the axis and (ii) outside the combined system.
View SolutionTwo long coaxical insulated solenoid's S1 and S2 of equal lengths are would one over the other as shown in figure. A steady current 'T' flows through the inner solenoid S1 to the other end B, which is connected to the outer solenoid S2 through which the same current flows in opposite direction so as to come out at end A. If n1 and n2 are the number of turns per unit length, find the magnitude and direction of net magnetic field at a point (i) inside on the axis and (ii) outside the combined system.

View SolutionIn the circuit shown in figure . (a) find the current flowing through the 100Ω resistor connecting points U and S.
View SolutionIn the circuit shown in the figure The steady state currents i1andi2 in the coils after the switch S is closed are

View Solution
