A steel ball of mass m falls in a viscous liquid with terminal velocity v, then the steel ball of mass 8m will fall in the same liquid with terminal velocity
v
4v
8v
16√2v
The correct Answer is:B
To solve the problem, we need to find the terminal velocity of a steel ball with mass 8m falling in a viscous liquid, given that a steel ball of mass m falls with terminal velocity v.
1. Understanding Terminal Velocity:
Terminal velocity (vt) is the constant speed reached by an object when the force of gravity is balanced by the drag force (viscous force) acting on it.
2. Forces Acting on the Ball:
When a ball falls through a viscous fluid, the forces acting on it are:
- Weight (W=mg) acting downwards.
- Upthrust (buoyant force) acting upwards.
- Viscous drag force (Fv) acting upwards.
At terminal velocity, these forces balance:
mg=Fv+Upthrust
3. Expression for Terminal Velocity:
The terminal velocity for a sphere falling through a viscous fluid can be expressed as:
vt=29r2(ρ−σ)gη
where:
- r = radius of the ball,
- ρ = density of the ball,
- σ = density of the fluid,
- g = acceleration due to gravity,
- η = coefficient of viscosity.
4. Relation Between Mass and Radius:
The mass of the ball is related to its volume and density:
m=ρball⋅V=ρball⋅43πr3
Thus, mass is proportional to the cube of the radius:
m∝r3⇒m1∝r31andm2∝r32
5. Finding the New Radius:
If the mass increases from m to 8m, we can set up the following relationship:
8m∝r′3⇒8⋅r3∝r′3
Taking the cube root:
r′=2r
6. Calculating the New Terminal Velocity:
Now, substituting r′=2r into the terminal velocity formula:
vt′=29(2r)2(ρ−σ)gη=294r2(ρ−σ)gη=4(29r2(ρ−σ)gη)=4vt
Since vt for mass m is v, we have:
vt′=4v
Conclusion:
The terminal velocity of the steel ball with mass 8m falling in the same viscous liquid will be 4v.
Terminal velocity (vt) is the constant speed reached by an object when the force of gravity is balanced by the drag force (viscous force) acting on it.
When a ball falls through a viscous fluid, the forces acting on it are:
- Weight (W=mg) acting downwards.
- Upthrust (buoyant force) acting upwards.
- Viscous drag force (Fv) acting upwards.
mg=Fv+Upthrust
The terminal velocity for a sphere falling through a viscous fluid can be expressed as:
vt=29r2(ρ−σ)gη
where:
- r = radius of the ball,
- ρ = density of the ball,
- σ = density of the fluid,
- g = acceleration due to gravity,
- η = coefficient of viscosity.
The mass of the ball is related to its volume and density:
m=ρball⋅V=ρball⋅43πr3
Thus, mass is proportional to the cube of the radius:
m∝r3⇒m1∝r31andm2∝r32
If the mass increases from m to 8m, we can set up the following relationship:
8m∝r′3⇒8⋅r3∝r′3
Taking the cube root:
r′=2r
Now, substituting r′=2r into the terminal velocity formula:
vt′=29(2r)2(ρ−σ)gη=294r2(ρ−σ)gη=4(29r2(ρ−σ)gη)=4vt
Since vt for mass m is v, we have:
vt′=4v
The terminal velocity of the steel ball with mass 8m falling in the same viscous liquid will be 4v.
Topper's Solved these Questions
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Level 1 Subjective
36 Videos
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Subjective Question
2 Videos
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Assertion and Reason
1 Videos
- EXPERIMENTSBOOK - DC PANDEY ENGLISHCHAPTER - EXPERIMENTSEXERCISE - Subjective
15 Videos
- GENERAL PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
Similar Questions
Knowledge Check
A metallic sphere of mass M falls through glycerine with a terminal velocity v. If we drop a ball of mass 8M of same metal into a column of glycerine, the terminal velocity of ball will be
A2vB4vC8vD16vAfter terminal velocity is reached the acceleration of a body falling through a viscous fluid is:
AzeroBequal to gCless than gDmore than g
Uniform speed of 2 cm diameter ball is 20cm/s in a viscous liquid. Then, the speed of 1 cm diameter ball in the same liquid is
View SolutionThe terminal velocity v of a spherical ball of lead of radius R falling through a viscous liquid varies with R such that
View SolutionA small sphere of volume V falling in a viscous fluid acquires a terminal velocity vt. The terminal velocity of a sphere of volume 8V of the same material and falling in the same fluid will be :
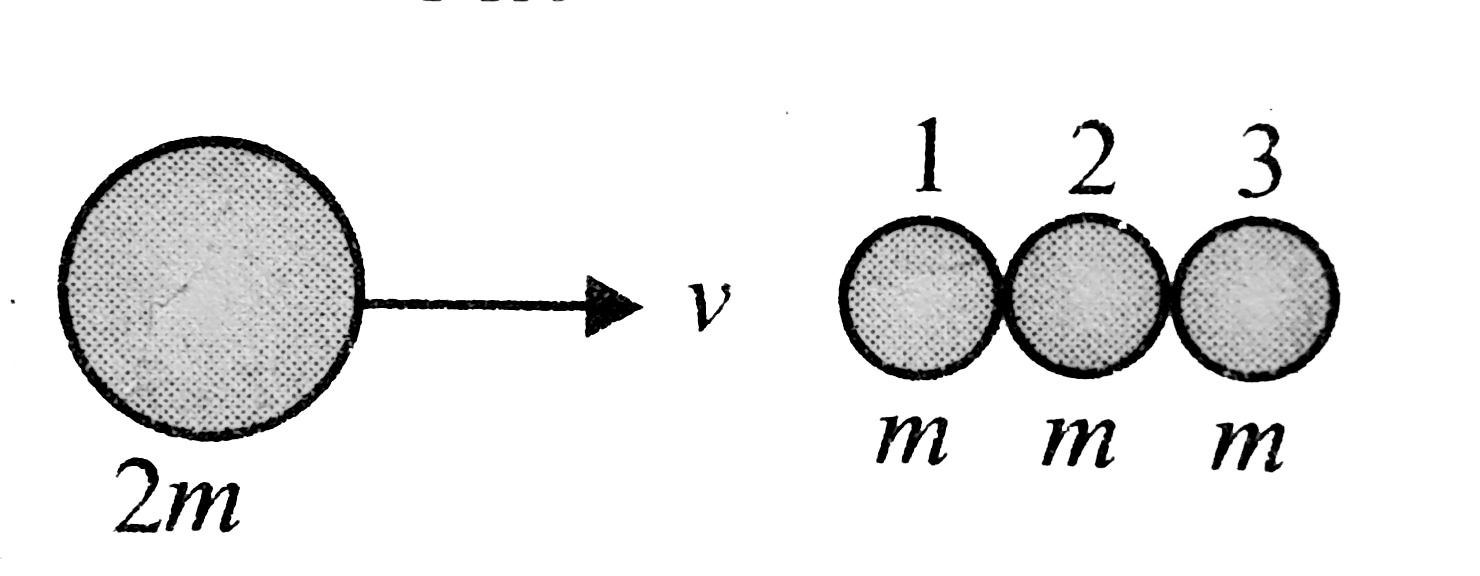
View SolutionA steel ball of mass 2m suffersone-dimensional elastic collision with a row of three steel balls, each of mass m. If mass 2m has collided with velocity v and the three balls numbered 1,2,3 were initially at 2. rest, then after the collision
View SolutionA spherical ball falls through viscous medium with terminal velocity v. If this ball is replaced by another ball of the same mass but half the radius, then the terminal velocity will be (neglect the effect of buoyancy.)
View SolutionA sphere of radius R is gently dropped into liquid of viscosity η in a vertical uniform tube. It attains a terminal velocity v. Another sphere of radius 2R when dropped into the same liquid, will attain its teriminal velocity.
View Solution
