Question

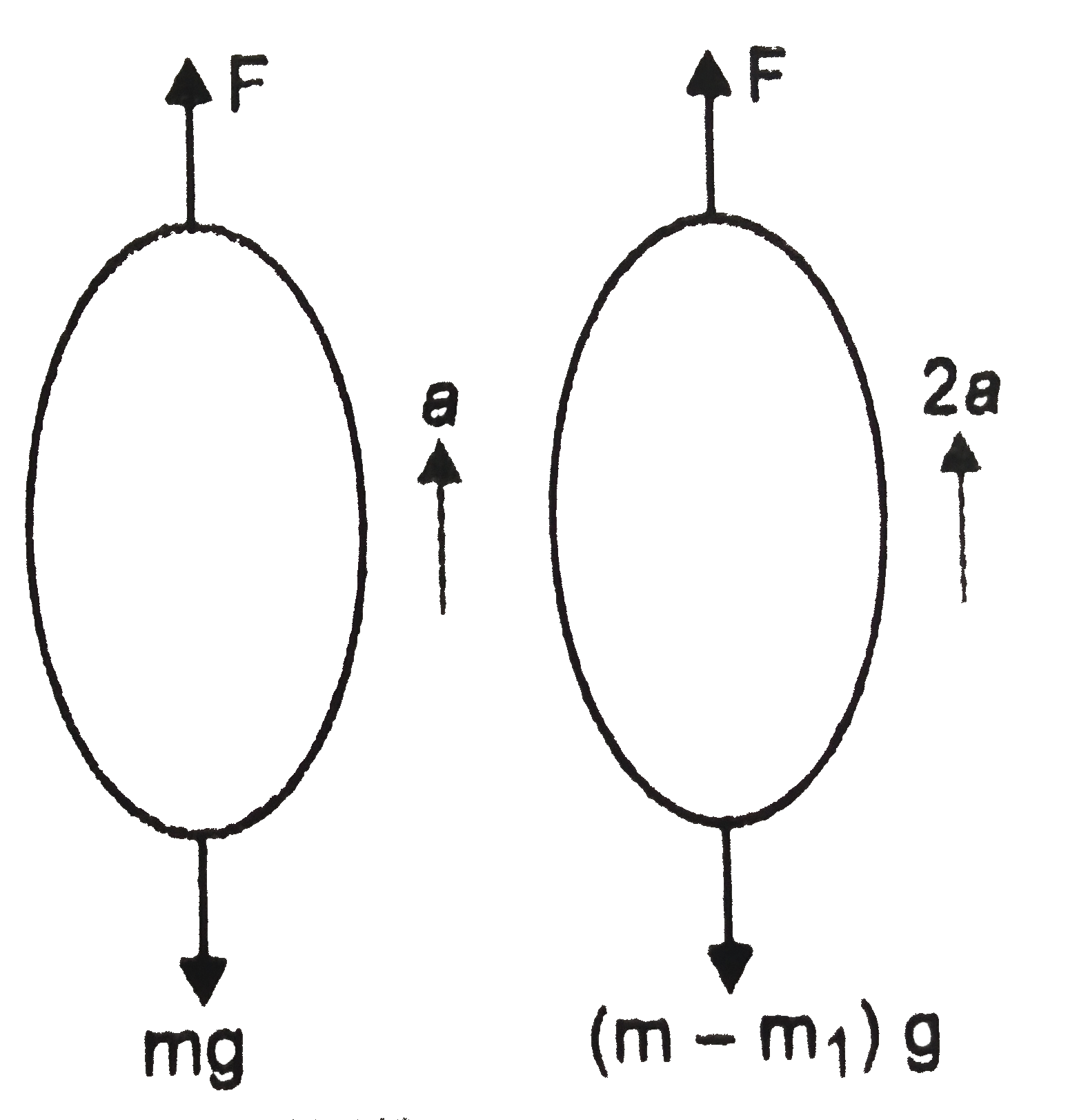
A balloon of mass M descends with an acceleration ${\displaystyle a_0}$. The mass that must be thrown out in order to give the balloon an equal upwards acceleration will be

Options

A. `(Ma_(0))/(g)`
B. `(2 Ma_(0))/(g)`
C. `(2 Ma_(0))/(g+a_(0))`
D. `(M(g+a_(0)))/(a_0)`

Answer

C

Explanation

To solve the problem of determining the mass that must be thrown out of a descending balloon to give it an equal upward acceleration, we can follow these steps:

1. Identify the Forces Acting on the Balloon:
- The weight of the balloon is given by \( W = Mg \), where \( M \) is the mass of the balloon and \( g \) is the acceleration due to gravity.
- The balloon is descending with an acceleration \( a_0 \).

2. Apply Newton's Second Law:
- When the balloon descends with an acceleration \( a_0 \), the net force acting on it can be expressed as:
\( F_{\text{net}} = Mg - F_{\text{buoyancy}} = Ma_0 \)
- Rearranging gives us:
\( F_{\text{buoyancy}} = Mg - Ma_0 \)

3. Consider the Situation After Throwing Mass:
- Let \( m \) be the mass that is thrown out of the balloon.
- The new mass of the balloon becomes \( M - m \).
- We want the balloon to ascend with an acceleration equal to \( a_0 \). The net force acting on the balloon now is:
\( F_{\text{net}} = F_{\text{buoyancy}} - (M - m)g = (M - m)a_0 \)

4. Set Up the Equation:
- From the buoyancy force, we have:
\( F_{\text{buoyancy}} = (M - m)g + (M - m)a_0 \)
- Setting the two expressions for buoyancy equal, we get:
\( Mg - Ma_0 = (M - m)g + (M - m)a_0 \)

5. Simplify and Solve for \( m \):
- Expanding the right side:
\( Mg - Ma_0 = Mg - mg + Ma_0 - ma_0 \)
- Rearranging gives us:
\( Ma_0 + mg - ma_0 = 0 \)
- Rearranging terms leads to:
\( m(a_0 + g) = 2Ma_0 \)
- Finally, solving for \( m \):
\( m = \frac{2Ma_0}{g + a_0} \)

Final Result:
The mass that must be thrown out to give the balloon an equal upward acceleration is:
\( m = \frac{2Ma_0}{g + a_0} \)