A body of weight w1 when floats in water displaces an amount of water w2. Then w1<w2. In this statement true or false?
The correct Answer is:A
To determine whether the statement "A body of weight w1 when floats in water displaces an amount of water w2. Then w1<w2" is true or false, we can analyze the situation step by step.
Step 1: Understand the concept of buoyancy
When a body floats in a fluid, it displaces a volume of fluid equal to the weight of the body. This is explained by Archimedes' principle, which states that the buoyant force acting on a submerged object is equal to the weight of the fluid that the object displaces.
Hint: Remember that buoyancy is the upward force exerted by the fluid on the submerged or floating body.
Step 2: Define the weights
Let:
- w1 = weight of the body
- w2 = weight of the water displaced by the body
Step 3: Apply Archimedes' Principle
According to Archimedes' principle, when the body is floating, the buoyant force Fb acting on the body is equal to the weight of the fluid displaced, which is w2. Therefore, we can write:
Fb=w2
Step 4: Relate buoyant force to the weight of the body
The buoyant force Fb is also equal to the weight of the body w1 when it is floating. Thus, we have:
w1=Fb
Step 5: Combine the equations
From the above two steps, we can equate the two expressions for the buoyant force:
w1=w2
Step 6: Evaluate the statement
The statement claims that w1<w2. However, from our analysis, we have found that w1=w2. Therefore, the statement is false.
Conclusion
The statement "A body of weight w1 when floats in water displaces an amount of water w2. Then w1<w2" is false.
---
When a body floats in a fluid, it displaces a volume of fluid equal to the weight of the body. This is explained by Archimedes' principle, which states that the buoyant force acting on a submerged object is equal to the weight of the fluid that the object displaces.
Let:
- w1 = weight of the body
- w2 = weight of the water displaced by the body
According to Archimedes' principle, when the body is floating, the buoyant force Fb acting on the body is equal to the weight of the fluid displaced, which is w2. Therefore, we can write:
Fb=w2
The buoyant force Fb is also equal to the weight of the body w1 when it is floating. Thus, we have:
w1=Fb
From the above two steps, we can equate the two expressions for the buoyant force:
w1=w2
The statement claims that w1<w2. However, from our analysis, we have found that w1=w2. Therefore, the statement is false.
The statement "A body of weight w1 when floats in water displaces an amount of water w2. Then w1<w2" is false.
Topper's Solved these Questions
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Subjective Question
2 Videos
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Level 2 Single Correct
36 Videos
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Level 1 Single Correct
49 Videos
- EXPERIMENTSBOOK - DC PANDEY ENGLISHCHAPTER - EXPERIMENTSEXERCISE - Subjective
15 Videos
- GENERAL PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
Similar Questions
Knowledge Check
A body of weight W is floating in a liquid. Its apparent weight will be :
Aequal to WBless than WCgreater than WDzeroFor a floating body, its weight W and upthrust FB on it are related as
AW>FBBW<FBCW=FBDnothing can be said
The weight of an object in the coal mine, sea level and at the top of the mountain are W1,W2 and W3 respectively, then
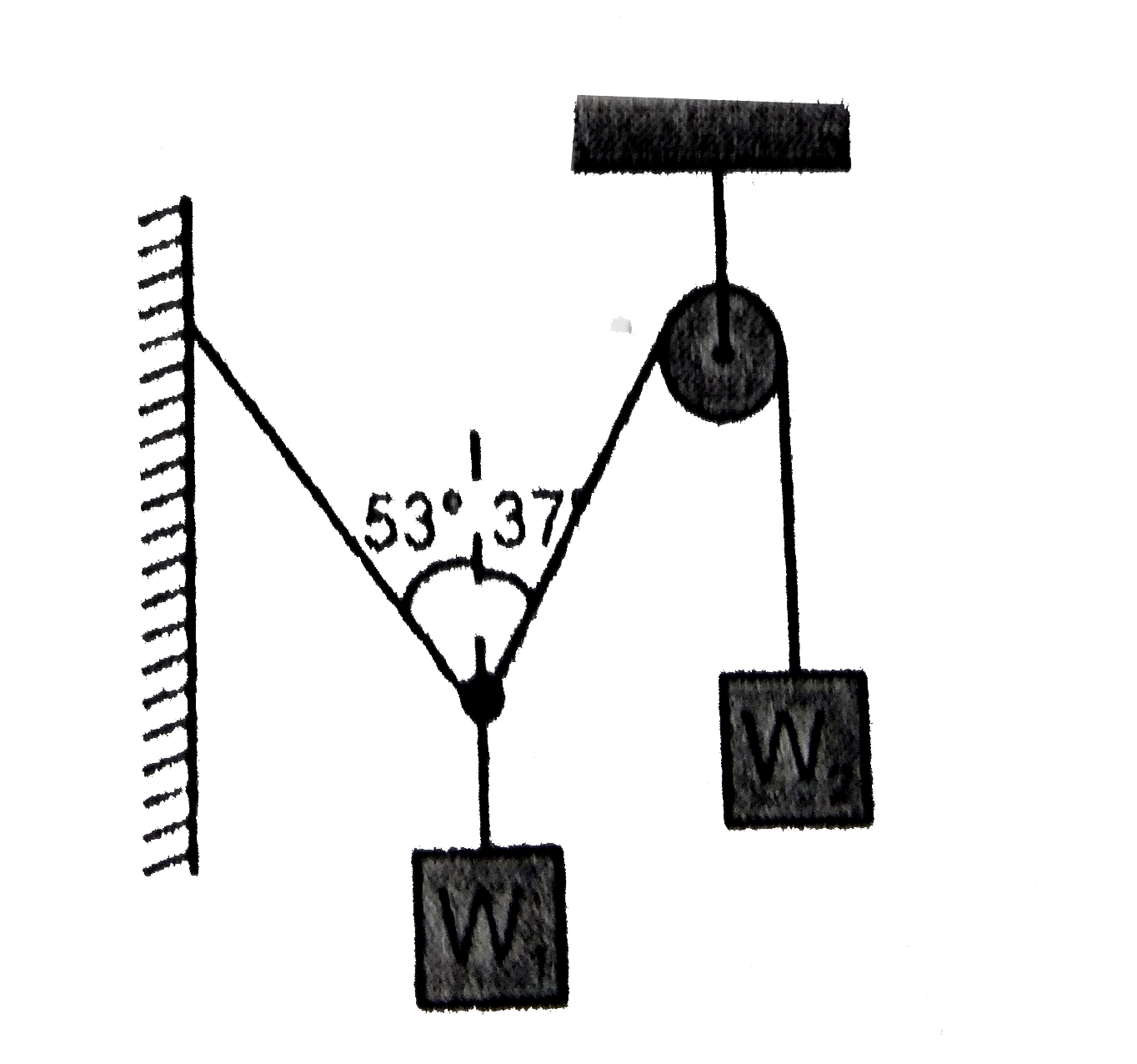
View SolutionTwo weights W1 and W2 in equilibrium and at rest, are suspended as shown in figure. Then the ratio W1W2 is :
View Solution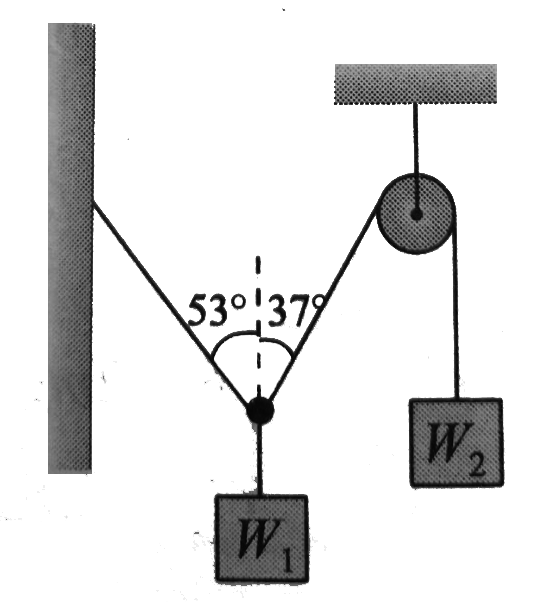
Two weights W1 and W2 in equilibrius and at rest are suspended as shown in figure. Then the ratio W1W2 is:
View SolutionA body weighs W1 in a liquid of density ρ1 and W2 in a liquid of density ρ2. What is the weight of body in a liquid of density ρ3?
View SolutionA body weighs W gf in air and W1 gf when it is completely immersed in water. Find (i) volume of the body (ii) upthrust on the body. (iii) relative density of material of the body.
View Solutionstatement-1: If water is heated of 50∘C then pH will increase.
STATEMENT-2: Kw increases with increase in temperature.
View Solution
