A steel wire of diameter 0.8 mm and length 1m is clamped firmly at two points P and Q which are one metre apart and in the same horizontal plane. A body is hung from the middle point of the wire, such that the middle point sags one cm lower from the original position as shown in figure. Calculate the mass of the body. $Y = 2 \times 10^{11} N / m^{2}$ .

Video Solution

Text Solution

Verified by Experts

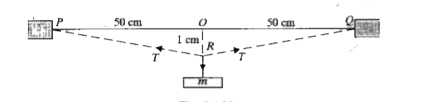
Let T be the tension in each segment of the wire and $∠ O R Q = ∠ O R P = θ$
$2 T cos θ = m g$
Stress $= \frac{T}{A}$ , T = Stress $\times A$
$T = Y \times$ Strain $\times$ A
$A = π d^{2} / 4$
From the triangle POR, $P R = \sqrt{P O^{2} + O R^{2}} = \sqrt{2500 + 1} = 50.01$ cm
Final length of the wire $= 50.01 + 50.01 = 100.02 c m$
Original length $= 100 c m$
Change in length = 0.02cm
Strain $= \frac{0.02}{100} = 2 \times 10^{- 4}$
$T = Y \times$ Strain $\times A$
$= 2 \times 10^{11} \times 2 \times 10^{- 4} \times 3.14 \times \frac{{(0.8 \times 10^{- 3})}^{2}}{4}$
= 20.096N
$m = \frac{2 T cos θ}{g} = \frac{2 \times 20.096 \times 1}{9.8 \times 50.01} = 0.082 k g$

Updated on:21/07/2023

A 14.5 kg mass, fastened to the end of a steel wire of unstretched length 1m, is whirled in a vertical circle with an angular velocity of $2 r e v . / s$ at the bottom of the circle. The cross-sectional area of the wire is $0.065 c m^{2}$ . Calculate the elongation of the wire when the mass is at the lowest point of its path $Y_{s t e e l} = 2 \times 10^{11} N m^{- 2}$ .
A0.52 mm
B1.52 mm
C2.52 mm
D3.52 mm