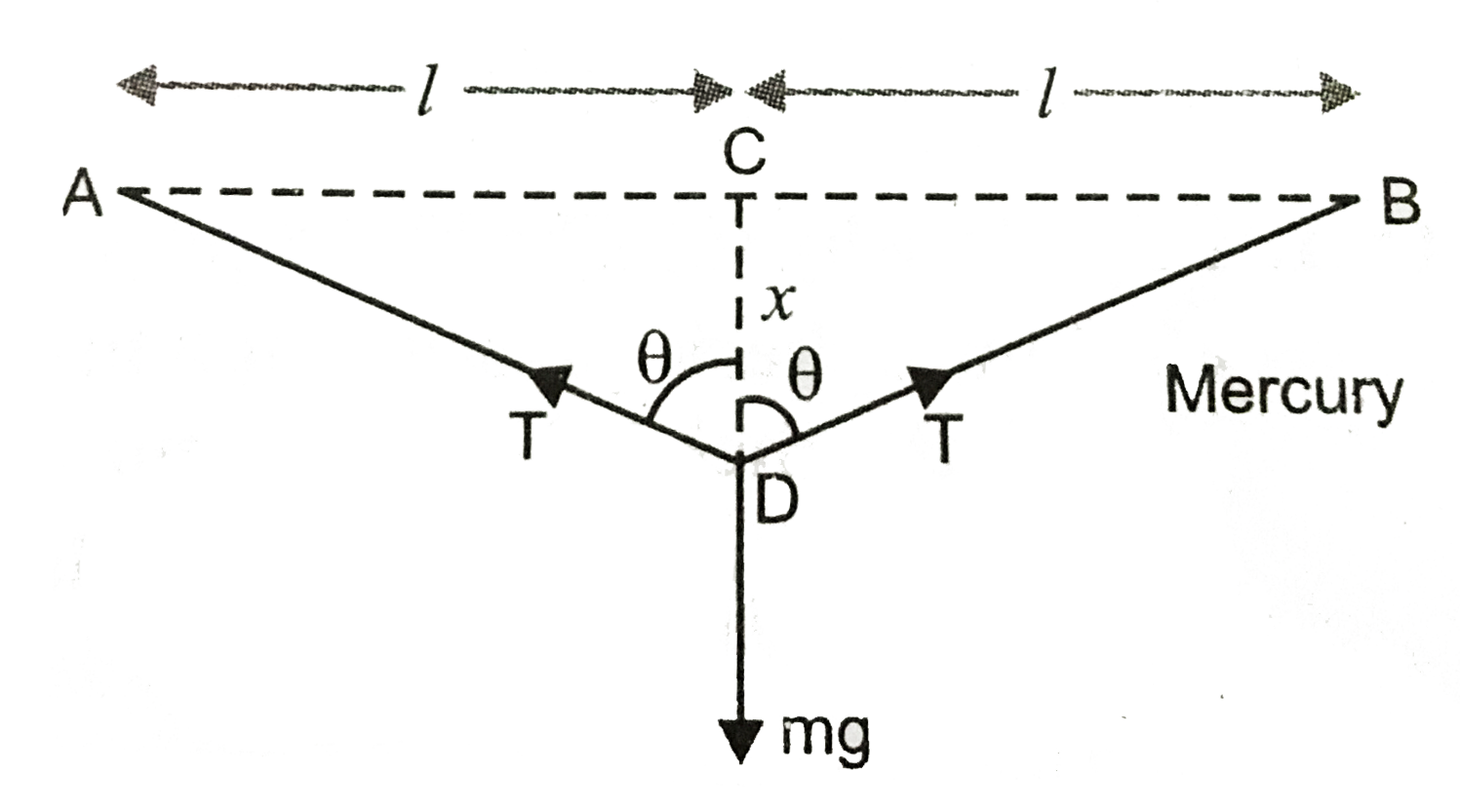
A steel wire of original length $1 m$ and cross-sectional area $4.00 m m^{2}$ is clamped at the two ends so that it lies horizontally and without tension. If a load of $2.16 k g$ is suspended from the middle point of the wire, what would be its vertical depression ?
Y of the steel $= 2.0 \times 10^{11} N m^{- 2}$ . Take $g = 10 m s^{- 2}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A, C

From $cos θ = \frac{X}{\sqrt{X^{2} + I^{2}}}$
$= \frac{X}{I} {1 + \frac{X^{2}}{I^{2}}}^{- \frac{1}{2}}$
$= X . I$ ….1
increase in length
$Δ L = (A C + C B) - A B$
here $A C =$ ( $I^{2}$ + $X^{2}$ )^(1/2)
So, $Δ L = 2 {(I^{2} + X^{2})}^{\frac{1}{20}}$
given that $A = 4 m m^{2}$
$= 4 \times 10^{- 2} c m^{2}$
Substituing the values we have
$Y = \frac{F}{A} \frac{L}{Δ L}$
$\to 2 \times 10612$
$= \frac{T \times 100}{(4 d x x 10^{- 2}) \times [2 {(50^{2} + X^{2})}^{\frac{1}{2}} - 100]}$ ........2
from equation i, ii and the freebody diagram ltbr> $2 T cos θ = m g$
$2 T (\frac{X}{50}) = 2.16 \times 10^{3} \times 980$
$= \frac{2 \times (2 \times 10^{12}) \times (4 \times 10^{- 2}) \times [2 (50^{2} + \frac{X^{21}}{2}) - 100 \times X]}{100 \times 50}$
$(2.16) \times 10^{3} \times 980$
Solving for X, we get X=1.5 cm.

|

Updated on:21/07/2023

Class 11 PHYSICS PROPERTIES OF SOLIDS AND FLUIDS

Topper's Solved these Questions

Similar Questions

HC VERMA ENGLISH-SOME MECHANICAL PROPERTIES OF MATTER-Exercises

Home
Ask Doubt
Profile