A stone dropped from the top of a tower travels 59 th of the height of tower during the last second of fall. Height of the tower is: (Take g=10m/s2)
A
52 m
B
36 m
C
45 m
D
78 m
Video Solution
Text Solution
The correct Answer is:C
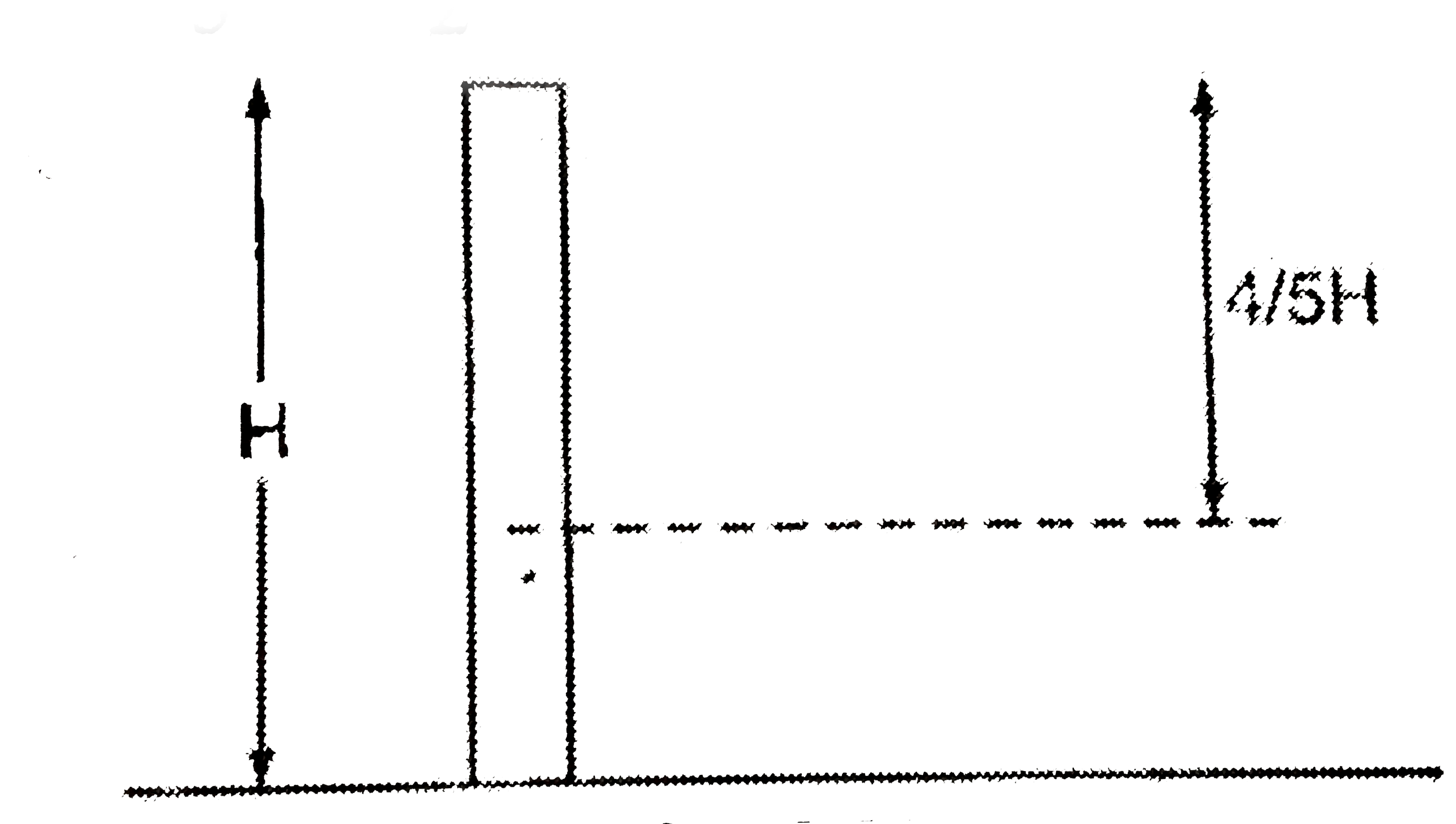
H=12gT2
45H=12g(T−1)2
|
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINEBOOK - GRB PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - More than one choice is correct
16 Videos
- MOTION IN A STRAIGHT LINEBOOK - GRB PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Assertion Reason
12 Videos
- MOTION IN A STRAIGHT LINEBOOK - GRB PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Problems and Practice
16 Videos
- FRICTION AND CIRCULAR MOTION BOOK - GRB PUBLICATIONCHAPTER - FRICTION AND CIRCULAR MOTION EXERCISE - Comprehension type
11 Videos
- MOTION IN TWO AND THREE DIMENSIONSBOOK - GRB PUBLICATIONCHAPTER - MOTION IN TWO AND THREE DIMENSIONSEXERCISE - All Questions
210 Videos
Similar Questions
Knowledge Check
A stone dropped form the top of a tower is found to travel (5/9) of the height of tower during last second of its fall. The time of fall is :
A2 sB3 sC4 sD5 sA ball rleased from the tope of a tower travels 1136 of the height of the tower in the last second of its journey. The height of the tower is (g= 10 ms^(2)).
A11mB(b) 36mC(c ) 180mD(d) 110 mA stone dropped from the top of a tower reaches the ground in 3 s. The height of the tower is
A18.6 mB39.2 mC44.1 mD98 m
A stone dropped from the top of the tower touches the ground in 4 sec. The height of the tower is about
View SolutionA body dropped from top of a tower fall through 60 m during the last two seconds of its fall. The height of tower is : (g=10m/s2)
View SolutionA body dropped from top of a tower fall through 60 m during the last two seconds of its fall. The height of tower is : (g=10m/s2)
View SolutionA stone is dropped from the top of a tower and travels 24.5 m in the last second of its journey.
Then the height of the tower is
View SolutionA body dropped from top of tower falls through 60 m during the last 2 seconds of its fall. The height of tower is (g=10m/s2)
View Solution
