A stone is let to fall from a balloon ascending with an acceleration f. After time t, a second stone is dropped. Prove that the distance between the stones after time t'
since the second stone is dropped, is 12(f+g)t(t+2t').
The correct Answer is:12(g+f)(t)(t+2t')
To solve the problem, we need to analyze the motion of two stones: the first stone that is dropped from a balloon and the second stone that is dropped after a time interval t.
Step 1: Understand the motion of the first stone
The first stone is released from a balloon that is ascending with an acceleration f. When the stone is released, it has an initial upward velocity equal to the velocity of the balloon at that moment. The acceleration acting on the stone after it is released is −g (downward).
Step 2: Calculate the distance traveled by the first stone
The first stone falls for a total time of t+t′ (where t′ is the time since the second stone is dropped). The distance s1 traveled by the first stone can be calculated using the equation of motion:
s1=ut+12at2
Here, u=0 (initial velocity relative to the balloon), a=−g (acceleration due to gravity), and the time is t+t′.
Thus,
s1=0+12(−g)(t+t′)2
However, we need to consider the initial upward velocity of the stone when it was released. The velocity of the balloon at the time of release is f⋅t, so the initial velocity u is f⋅t. Therefore, we have:
s1=(f⋅t)(t+t′)+12(−g)(t+t′)2
Step 3: Calculate the distance traveled by the second stone
The second stone is dropped after time t from the balloon. It starts from rest relative to the balloon, so its initial velocity is 0. The distance s2 traveled by the second stone in time t′ is given by:
s2=0+12(−g)(t′)2
Again, we need to consider the relative motion. The second stone is also affected by the upward acceleration of the balloon, so we have:
s2=12(g+f)(t′)2
Step 4: Find the distance between the two stones
The distance D between the two stones after time t′ since the second stone is dropped is given by:
D=s1−s2
Substituting the expressions for s1 and s2:
D=((f⋅t)(t+t′)−12g(t+t′)2)−(12(g+f)(t′)2)
Step 5: Simplify the expression
Now we simplify the expression:
D=(f⋅t)(t+t′)−12g(t+t′)2−12(g+f)(t′)2
This can be rearranged and simplified to yield:
D=12(f+g)t(t+2t′)
Final Result
Thus, the distance between the stones after time t′ since the second stone is dropped is:
D=12(f+g)t(t+2t′)
The first stone is released from a balloon that is ascending with an acceleration f. When the stone is released, it has an initial upward velocity equal to the velocity of the balloon at that moment. The acceleration acting on the stone after it is released is −g (downward).
The first stone falls for a total time of t+t′ (where t′ is the time since the second stone is dropped). The distance s1 traveled by the first stone can be calculated using the equation of motion:
s1=ut+12at2
Here, u=0 (initial velocity relative to the balloon), a=−g (acceleration due to gravity), and the time is t+t′.
s1=0+12(−g)(t+t′)2
However, we need to consider the initial upward velocity of the stone when it was released. The velocity of the balloon at the time of release is f⋅t, so the initial velocity u is f⋅t. Therefore, we have:
s1=(f⋅t)(t+t′)+12(−g)(t+t′)2
The second stone is dropped after time t from the balloon. It starts from rest relative to the balloon, so its initial velocity is 0. The distance s2 traveled by the second stone in time t′ is given by:
s2=0+12(−g)(t′)2
Again, we need to consider the relative motion. The second stone is also affected by the upward acceleration of the balloon, so we have:
s2=12(g+f)(t′)2
The distance D between the two stones after time t′ since the second stone is dropped is given by:
D=s1−s2
Substituting the expressions for s1 and s2:
D=((f⋅t)(t+t′)−12g(t+t′)2)−(12(g+f)(t′)2)
Now we simplify the expression:
D=(f⋅t)(t+t′)−12g(t+t′)2−12(g+f)(t′)2
This can be rearranged and simplified to yield:
D=12(f+g)t(t+2t′)
Thus, the distance between the stones after time t′ since the second stone is dropped is:
D=12(f+g)t(t+2t′)
Topper's Solved these Questions
- KINEMATICS-1Book:CENGAGE PHYSICS ENGLISHChapter:KINEMATICS-1Exercise:Single Correct
Explore 52 Videos
- KINEMATICS-1Book:CENGAGE PHYSICS ENGLISHChapter:KINEMATICS-1Exercise:Graphical Concept
Explore 17 Videos
- KINEMATICS-1Book:CENGAGE PHYSICS ENGLISHChapter:KINEMATICS-1Exercise:Exercise 4.4
Explore 16 Videos
- GRAVITATIONBook:CENGAGE PHYSICS ENGLISHChapter:GRAVITATIONExercise:INTEGER_TYPE
Explore 1 Video
- KINEMATICS-2Book:CENGAGE PHYSICS ENGLISHChapter:KINEMATICS-2Exercise:Exercise Integer
Explore 9 Videos
Similar Questions
A stone is let to fall from a balloon ascending with acceleration 4ms2. After time t=2s, a second stone is dropped. If the distance between the stones after time (t′=3s) since the second stone is dropped is d, find d28
View SolutionA balloon in ascending vertically with an acceleration of 1ms−2. Two stones are dropped from it at an interval of 2s. Find the distance berween them 1.5s after the second stone is released.
View SolutionA balloon a ascending vertically with an acceleration of 0.4m/s2. Two stones are dropped from it at an interval of 2sec. Find the distance between them 1.5sec. after the second stone is released. (g=10m/sec2).
View SolutionA stone is released from a rising balloon accelerating upward with acceleration a. The acceleration of the stone just after the release is
View SolutionA stone is released from an elevator going up with an acceleration of g2. What is the acceleration of the stone just after release ?
View SolutionA stone is dropped from a balloon ascending with v0=2ms, from a height h=4.8 m .Find the time of flight of the stone.
View SolutionA balloon starts rising from ground from rest with an upward acceleration 2m/s2. Just after 1 s, a stone is dropped from it. The time taken by stone to strike the ground is nearly
View SolutionA balloon starts rising upwards with constant acceleration a and afrer time t0, second, a packet is dropped from it which reaches the ground aftre t seconds of dropping . Derermine the value of t
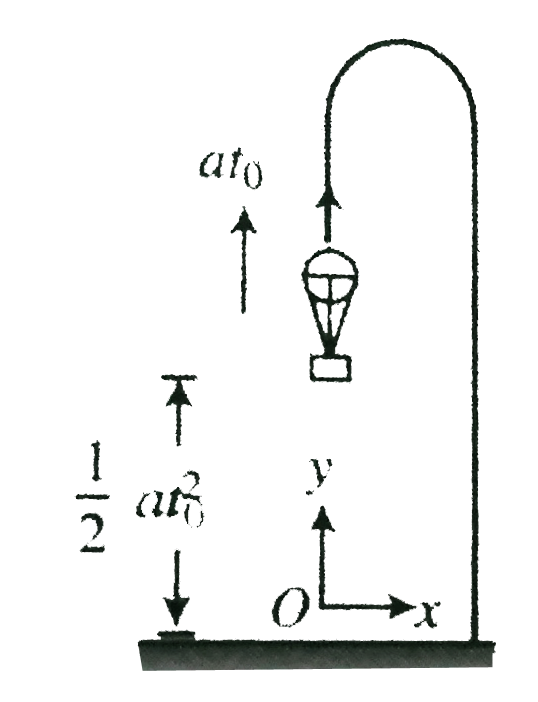 .
.
View SolutionA balloon rises from rest on the ground with constant acceleration g/8. A stone is dropped from the balloon when the balloon has risen to a height of (H). Find the time taken by the stone to reach the ground.
View SolutionA stone is dropped from the top of a tower. If it hits the ground after 10 seconds, what is the height of the tower?
View Solution