A stone is projected from the ground with velocity 50ms at an angle of 30∘. It crosses a wall after 3 sec. How far beyond the wall the stone will strike the ground (g=10msec2?
90.2m
89.6m
86.6m
70.2m
The correct Answer is:C
Step by step video, text & image solution for A stone is projected from the ground with velocity 50(m)/(s) at an angle of 30^@. It crosses a wall after 3 sec. How far beyond the wall the stone will strike the ground (g=10(m)/(sec^2)? by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A particle is projected from the ground with an initial velocity of 20m/s at angle fo 30∘ with the horizontal. What is the magnitude of chang in velocity in 0.5scond ? ( g= 10 m//s^2).
View SolutionThe surface of a hill is inclined at an angle α to the horizontal .A stone is thrown from the summit of the hill at an angle β to the vertical with velocity v0.How far from the summit will the stone strike the ground ?
View Solution
Knowledge Check
A stone is projected from the ground with velocity 25m/s . Two seconds later, it just clears a wall 5 m high. The angle of projection of the stone is (g=10m/sec2)
A30∘B45∘C50.2∘D60∘A stone is projected from the ground with a velocity of 14ms−1. One second later it clears a wall 2m high. The angle of projection is (g=10ms−2)
A45∘B30∘C60∘D15∘A ball is projected from a point O as shown in figure it will strike the ground after (g = 10 m/s2 )
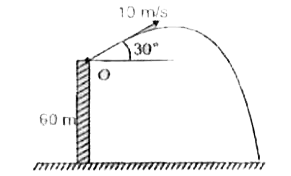 A4 sB3 sC2 sD5 s
A4 sB3 sC2 sD5 s
The surface of a hill is inclined at an angle α to the horizontal (Fig.). A stone is thrown from the summit of the hill at an initial speed v0 at an angle β to the vertical. How far from the summit will the stone strike the ground?
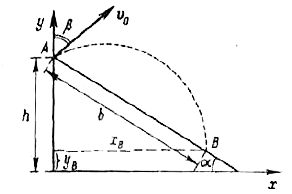
View SolutionA helicopter while flying at a height of 100 m with velocity 30 m.s at an angle 30∘ with the horizontal, drops a packet. Where will the packet strike the ground ? ( g = 10 m/s2)
View SolutionA ball is projected from a point O as shown in figure. It will strike the ground after (g = 10 m/s2)
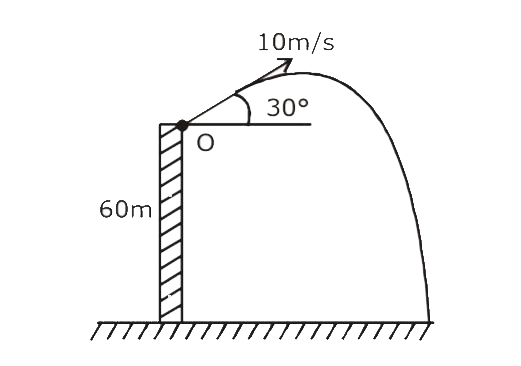
View Solution
A stone projected at an angle of 60∘ from the ground level strikes at an angle of 30∘ on the roof of a building of height h. Then the speed of projection of the stone is:
View SolutionA particle A is projected from the ground with an initial velocity of 10m/s at an angle of 60∘ with horizontal. From what height should an another particle B be projected horizontally with velocity 5m/s so that both the particles collide in ground at point C if both are projected simultaneously g=10m/s2.
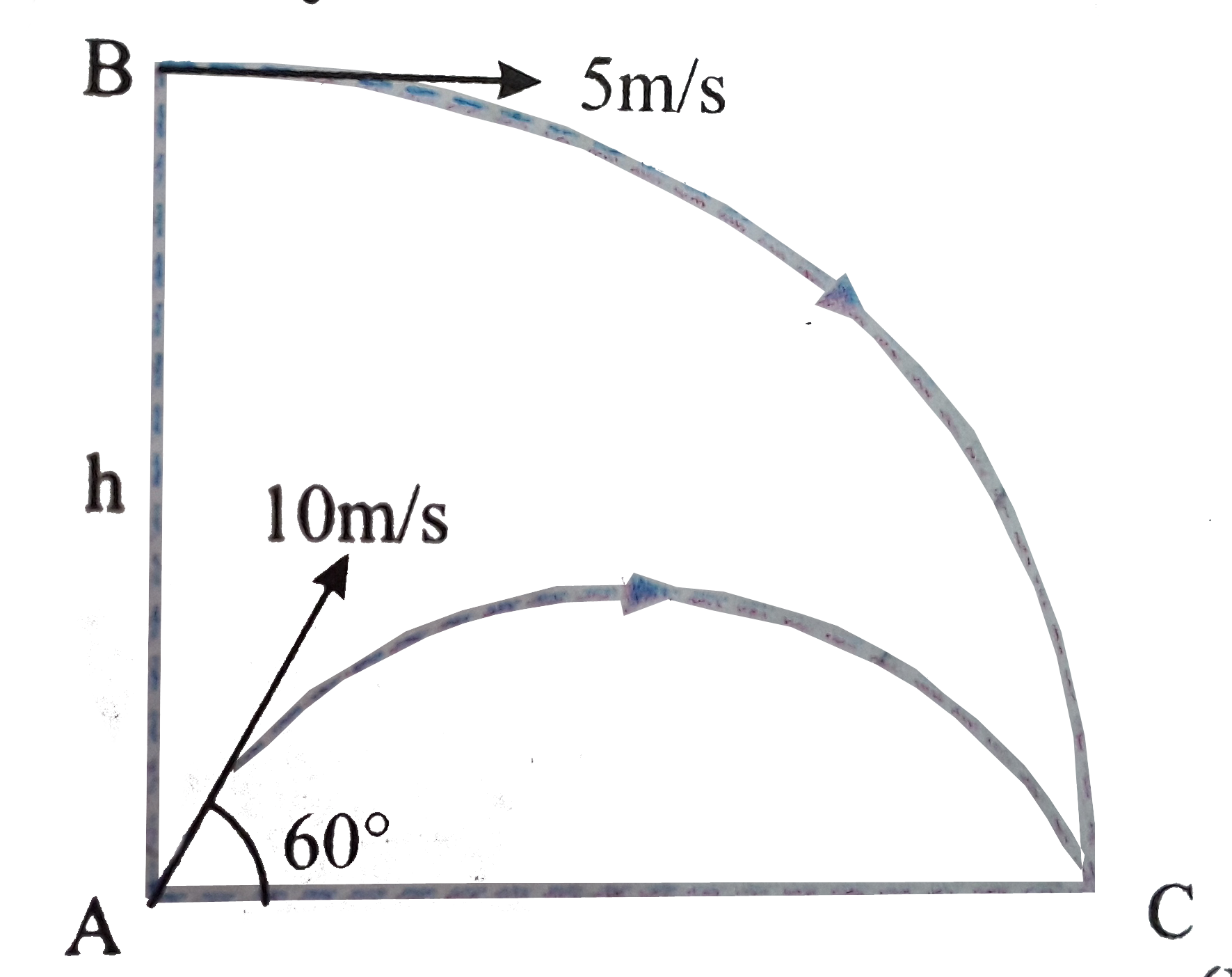
View Solution
