A stone is thrown by a student from the bottom of a hill with a velocity 30ms−1 making an angle of 60∘ with the horizontal. If the slpe of the hill is 30∘ with the horizontal. Find the distance from the student to a point at which the stone fals on hill, use g=10ms−2.
Refr to Art. 2 (d) .9, the distance
coverd on slope is R=2u2cosθsin(θ−θ0)gcos2θ0
Here, u=30ms−1
θ=60∘,θ=30∘,g=10ms−2
:. R=(2×302cos60∘sin960∘−30∘))10×cos230(#)
=2×900×(1/2)×(1/2)10×(√3/2)2
=69m.
Topper's Solved these Questions
- KINEMATICSBOOK - PRADEEPCHAPTER - KINEMATICSEXERCISE - 1 Conceptual Problems
2 Videos
- KINEMATICSBOOK - PRADEEPCHAPTER - KINEMATICSEXERCISE - 1 Con ceptual Problems
14 Videos
- KINEMATICSBOOK - PRADEEPCHAPTER - KINEMATICSEXERCISE - 3 SolvedExamples
46 Videos
- GRAVIATIONBOOK - PRADEEPCHAPTER - GRAVIATIONEXERCISE - Assertion-Reason Type Questions
19 Videos
- LAWS OF MOTIONBOOK - PRADEEPCHAPTER - LAWS OF MOTIONEXERCISE - Assertion- Reason Type Questions
17 Videos
Similar Questions
An object is projected with a velocity of 30ms−1 at an angle of 60∘ with the horizontal. Determine the horizontal range covered by the object.
View SolutionA body is projected with a velocity of 30ms−1 at an angle of 30∘ with the vertical. Find the maximum height, time of flight and the horizontal range.
View Solution
Knowledge Check
A stone is thrown from the top of a tower of height 50m with a velocity of 30ms−1 at an angle of 30∘ above the horizontal.Find the time during which the stone will be in air
A2secB3secC4secD5secA stone is projected with speed of 50ms−1 at an angle of 60∘ with the horizontal. The speed of the stone at highest point of trajectory is
A75ms−1B25ms−1C50ms−1Dcannot findA body is projected down from height of 60 m with a velocity 10ms−1 at angle 30∘ to horizontal. The time of flight of the body is [g=10ms−2]
A1sB2sC3sD4s
A stone is thrown up from the top of a tower 20,m with a velocity of 24m/s a tan elevation of 30∘ above the horizontal. Find the horizontal distance from the foot of the tower to the point at which the stone hits the ground. Take g=10m/s2
View SolutionA particle is thrown at time t = 0 with a velocity of 10ms−1 at an angle 60∘ with the horizontal from a point on an inclined plane, making an angle of 30∘ with the horizontal. The time when the velocity of the projectile becomes parallel to the incline is
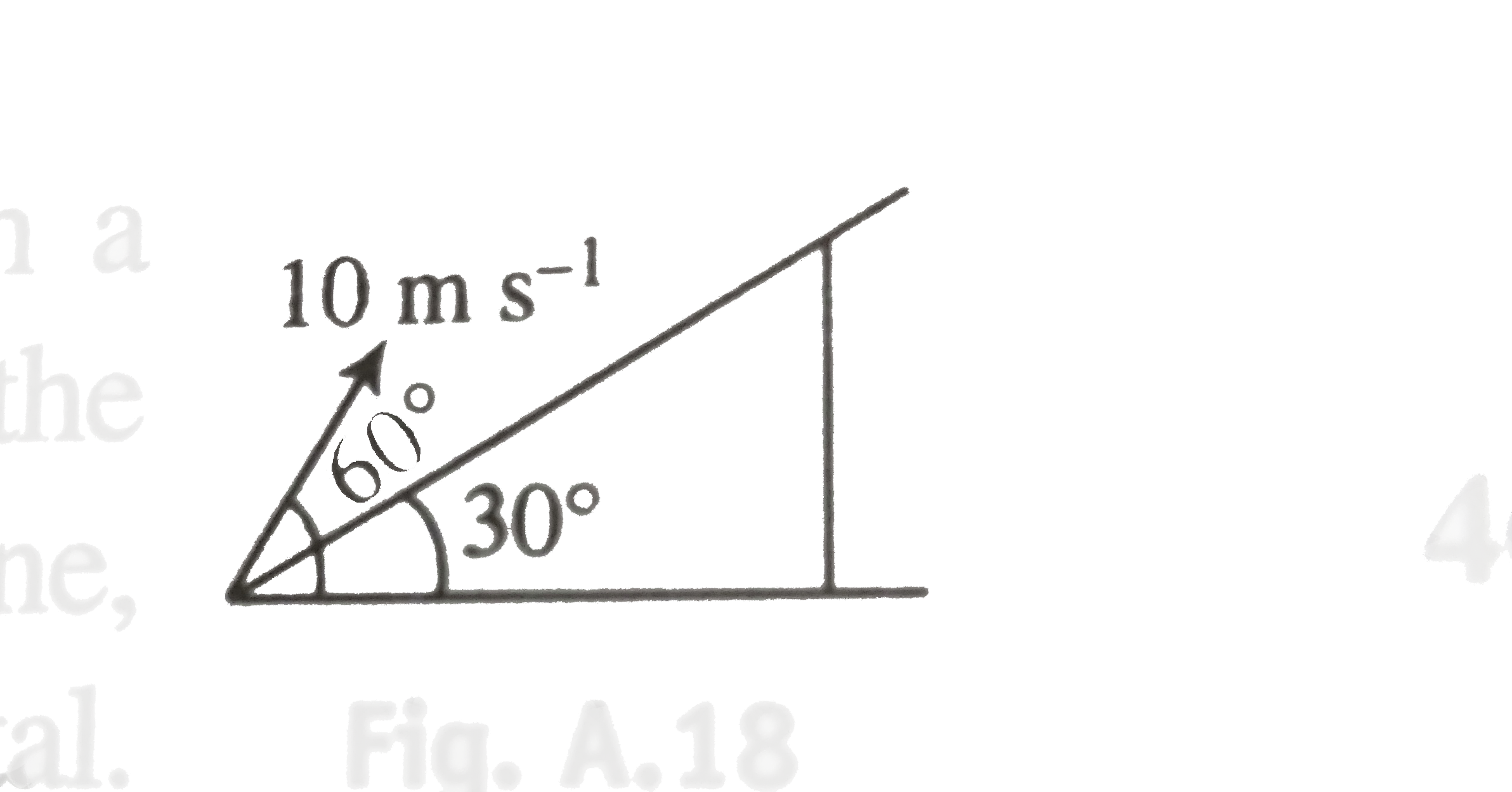
View SolutionA projectile is projected at 10ms−1 by making an angle 60∘ to the horizontal. After sometime, its velocity makes an angle of 30∘ to the horzontal . Its speed at this instant is:
View SolutionA particle is thrown at time t=0 with a velocity of 10 m/s at an angle of 60∘ with the horizontal from a point on an incline plane, making an angle of 30∘ with the horizontal. The time when the velocity of the projectile becomes parallel to the incline is :
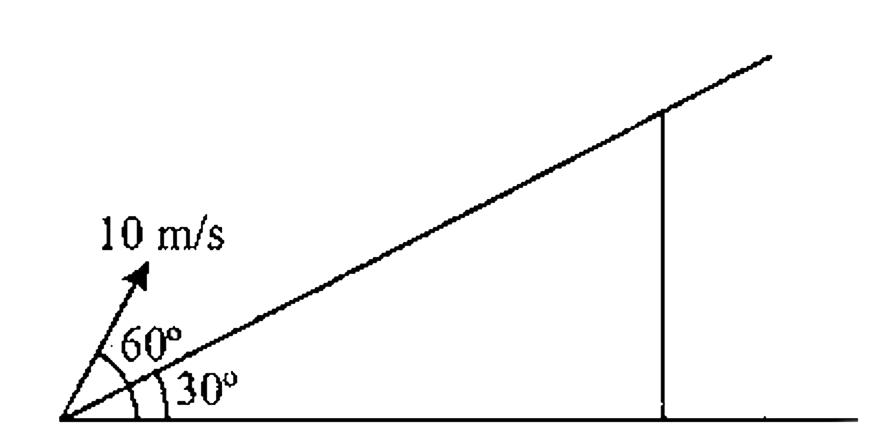
View SolutionA ball is thrown from the top of tower with an initial velocity of 10ms−1 at an angle of 30∘ with the horizontal. If it hits the ground of a distance of 17.3m from the back of the tower, the height of the tower is (Takeg=10ms−2)
View Solution
