A stone is tied to an elastic string of negligible mass and spring constant k. The unstretched length of the string is L and has negligible mass. The other end of the string is fixed to a nail at a point P. Initially the stone is at the same level as the point P. The stone is dropped vertically from point P.
(a) Find the distance 'y' from the top when the mass comes to rest for an instant, for the first time.
(b) What is the maximum velocity attained by the stone in this drop ?
(c) What shall be the nature of the motion after the stone has reached its lowest point ?Solution in Gujrati
Consider the diagram, the stone is dropped from point P.
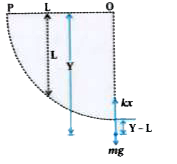
Stone is in free fall upto length L. After that elasticity of string exerted force for SHM. Suppose, stone is at rest at instantaneous distance .y..
Loss in potential energy of stone = Gain in elastic potential energy in string.
mgy=12k(y−L)2
∴mgy=12ky2−kyL+12kL2
⇒12ky2−(kL+mg)+12kL2=0
y=(kL+mg)±√(kL+mg)2−k2L2k
∴y=(kL+mg)±√2mgkL+m2g2k
∴y=(kL+mg)+√2mkL+m2g2k
(Taking .+. sign only)
(b) In SHM, the maximum velocity is attained when the body passes, through the "equilibrium positon". Means, at that time the instantaneous acceleration is zero. That is mg−kx=0, where x is the extension from L, ∴mg=kx
If v is the velocity, then
12mv2+12kx2=mg(L+x)
(From the law of conservation of energy)
12mv2=mg(L+x)−12kx2
Now mg=kx⇒x=mgk
∴12mv2=mg(L+mgk)−12km2g2k=mgL+m2g2k−12m2g2k
12mv2=mgL+12m2g2k
∴v2=2gL+mg2k
v=(2gL+mg2k)1/2
(c) When stone is at the lowest point Q, means at instantaneous distance Y from P from where the stone is dropped, then equation of motion of the stone is,
md2ydt2=mg−k(y−L)
⇒d2ydt2+km(y−L)−g=0
Put another variable,
z=km(y−L)−g
∴d2zdt2+kmz=0
This is second dervative equation which indicates SHM.
Comparing this equation with
d2zdt2+ω2=0
Angular frequency ω=√km
Equation simplify as under,
z=Acos(ωt+ϕ),
where ω√km
y=(L+mgk)+A.cos(ωt+ϕ)
Hence, stone will execute SHM with angular frequency ω=√km about the point
y0=L+mgk
Topper's Solved these Questions
- MACHANICAL PROPERTIES OF SOLIDS BOOK - KUMAR PRAKASHANCHAPTER - MACHANICAL PROPERTIES OF SOLIDS EXERCISE - SECTION-E
28 Videos
- MACHANICAL PROPERTIES OF SOLIDS BOOK - KUMAR PRAKASHANCHAPTER - MACHANICAL PROPERTIES OF SOLIDS EXERCISE - SECTION-F
11 Videos
- MACHANICAL PROPERTIES OF SOLIDS BOOK - KUMAR PRAKASHANCHAPTER - MACHANICAL PROPERTIES OF SOLIDS EXERCISE - SECTION-C
66 Videos
- LAW OF MOTIONBOOK - KUMAR PRAKASHANCHAPTER - LAW OF MOTIONEXERCISE - (QUESTION PAPER) SECTION-D
1 Videos
- MECHANICAL PROPERTIES OF FLUIDS BOOK - KUMAR PRAKASHANCHAPTER - MECHANICAL PROPERTIES OF FLUIDS EXERCISE - QUESTION PAPER (SECTION -C)
3 Videos
Similar Questions
Two wires A and B are of the same material their lengths are in the ratio 1 : 2 and the diameter are in the ratio 2 : 1. If they are pulled by the same force, their increase in length will be in the ratio ........
View SolutionTwo wires are made of the same material and have the same volume. The first wire has cross sectional area A and the second wire has cross sectional area 3A. If the length of the first wire is increased by Δl on applying a force F, how much force needed to stretch the second wire by the same amount ?
View SolutionWhat is elasticity ? What is plastic body and plasticity?
View SolutionA 70 kg man stands in contact against the inner wall of a hollow cylindrical drum of radius 3 m rotating about its vertical axis with 200 rev/min. The coefficient of friction between the wall and his clothing is 0.15. What is the minimum rotational speed of the cylinder to enable the man to remain stuck to the wall (without falling) when the floor is suddenly removed ?
View SolutionGlycerine flows steadily through a horizontal tube of length 1.5m and radius 1.0 cm . If the amount of glycerine collected per second at one is 4.0×10−3kgs−1 , what is the pressure difference between the two ends of the tube ? (Density of glycerine =1.3×10103kgm−3 and viscosity of glycerine =0.83 Pa s). [ you may also like to check if the assumption of laminar flow in the tube is correct]
View SolutionA stone of mass m tied to a string of length l is rotated in a circle with the other end of the string as the centre. The speed of the stone is v. If the string breaks, the stone will move
View SolutionA child revolves a stone of mass 0 .5 kg tied to the end of a string of length 40 cmin a vertical circle . The speed of the stone at the lowest point of the circle is 3 m//s Calculate tension in the string at this point.
View SolutionA stone of mass m is tied to a string of length l and rotated in a circle with a constant speed v . If the string is released, the stone flies
View SolutionA mass is attached to the end of a string of length l which is tied to a fixed point O. The mass is released from the initial horizontal position of the string. Below the point O at what minimum distance a peg P should be fixed so that the mass turns about P and can describe a complete circle in the vertical plane?
View SolutionA stone of a mass m tied to a string of length /is rotated in a circle with the other end of the string as the centre. The speed of the stone is V. If the string breaks, the stone will
View SolutionA stone of mass m is tied to an elastic string of negligble mass and spring constant k. The unstretched length of the string is L and has negligible mass. The other end of the string is fixed to a nail at a point p. Initially the stone is at the same level as the point P. The stone is dropped vertically from point P.
(a) Find the distance y from the top when the mass comes to rest for an instant, for the first time.
(b) What is the maximum velocity attained by the stone in this drop?
(c) What shall be the nature of the motion after the stone has reached its lowest point?
View Solutionनगण्य द्रव्यमान का एक पत्थर एक डोरी के सिरे से बाँधकर क्षैतिज वृत्त में घुमाया जा रहा हैं । यदि डोरी टूट जाये तो पत्थर गति करेगा -
View Solutionडोरी के एक रइरेसे बंधा हुवे द्रव्यमान m का एक पत्थर ताल में घुमाया जाता है । पत्थर के पथ में उचतम बिंदु पर डोरी में तनाव शून्य है । निम्नतम बिंदु पर डोरी में तनाव क्या होगा ?
View SolutionA stone of mass m is tied to a string and is moved in a vertical circle of radius r making n revolution per minute. The total tension in the string when the stone is its lowest point is.
View SolutionA child revolves a stone of mass 0.5 kg tied to the end of a string of length 40 cm in a vertical circle. The speed of the stone at the lowest point of the circle is 2 m/s calculate the tension in the string at this point.
View Solution
