A mass is attached to the end of a string of length l which is tied to a fixed point O. The mass is released from the initial horizontal position of the string. Below the point O at what minimum distance a peg P should be fixed so that the mass turns about P and can describe a complete circle in the vertical plane?
The correct Answer is:A
To solve the problem step by step, we will analyze the motion of the mass attached to the string and determine the minimum distance X from point O where the peg P should be fixed.
Step 1: Understand the Initial Setup
- A mass m is attached to a string of length l and is released from a horizontal position.
- The mass will swing downwards and will reach a vertical position below point O.
Step 2: Identify the Energy Conservation
- At the initial position (horizontal), the potential energy (PE) is maximum, and kinetic energy (KE) is zero.
- When the mass reaches the vertical position (point B), it has converted some potential energy into kinetic energy.
Step 3: Calculate Potential and Kinetic Energy
- Initial potential energy at point A (horizontal position):
UA=mgh=mg⋅l
- Kinetic energy at point B:
KB=12mv2
- By conservation of mechanical energy:
UA+KA=UB+KB
Since KA=0 (mass is at rest initially):
mg⋅l=0+12mv2
Simplifying gives:
v2=2gl(Equation 1)
Step 4: Determine Conditions for Completing the Circle
- For the mass to complete a vertical circle around peg P, the speed v at the top of the circle must satisfy:
v2≥5gR
where R=l−X (the radius of the circle after the peg).
- Thus, we have:
v2≥5g(l−X)(Equation 2)
Step 5: Set Up the Inequality
- From Equations 1 and 2, we equate:
2gl≥5g(l−X)
- Dividing through by g (assuming g≠0):
2l≥5(l−X)
Step 6: Solve for X
- Expanding the right side:
2l≥5l−5X
- Rearranging gives:
5X≥5l−2l
5X≥3l
- Dividing by 5:
X≥3l5
Conclusion
The minimum distance X from point O where the peg P should be fixed is:
X=3l5
- A mass m is attached to a string of length l and is released from a horizontal position.
- The mass will swing downwards and will reach a vertical position below point O.
- At the initial position (horizontal), the potential energy (PE) is maximum, and kinetic energy (KE) is zero.
- When the mass reaches the vertical position (point B), it has converted some potential energy into kinetic energy.
- Initial potential energy at point A (horizontal position):
UA=mgh=mg⋅l
- Kinetic energy at point B:
KB=12mv2
- By conservation of mechanical energy:
UA+KA=UB+KB
Since KA=0 (mass is at rest initially):
mg⋅l=0+12mv2
Simplifying gives:
v2=2gl(Equation 1)
- For the mass to complete a vertical circle around peg P, the speed v at the top of the circle must satisfy:
v2≥5gR
where R=l−X (the radius of the circle after the peg).
- Thus, we have:
v2≥5g(l−X)(Equation 2)
- From Equations 1 and 2, we equate:
2gl≥5g(l−X)
- Dividing through by g (assuming g≠0):
2l≥5(l−X)
- Expanding the right side:
2l≥5l−5X
- Rearranging gives:
5X≥5l−2l
5X≥3l
- Dividing by 5:
X≥3l5
The minimum distance X from point O where the peg P should be fixed is:
X=3l5
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Match the columns3videos
CIRCULAR MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Medical entrances s gallery19videos
CIRCULAR MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Check point45videos
CIRCULAR MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Subjective21videos
CENTRE OF MASS, LINEAR MOMENTUM AND COLLISION
- BOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Only One Option is Correct27videos
COMMUNICATION SYSTEM
Similar Questions
A particle of mass 1kg is attached to a string of length 5m. The string is attached to a fixed point O. It is released from theposition as shown in Fig. Calculate
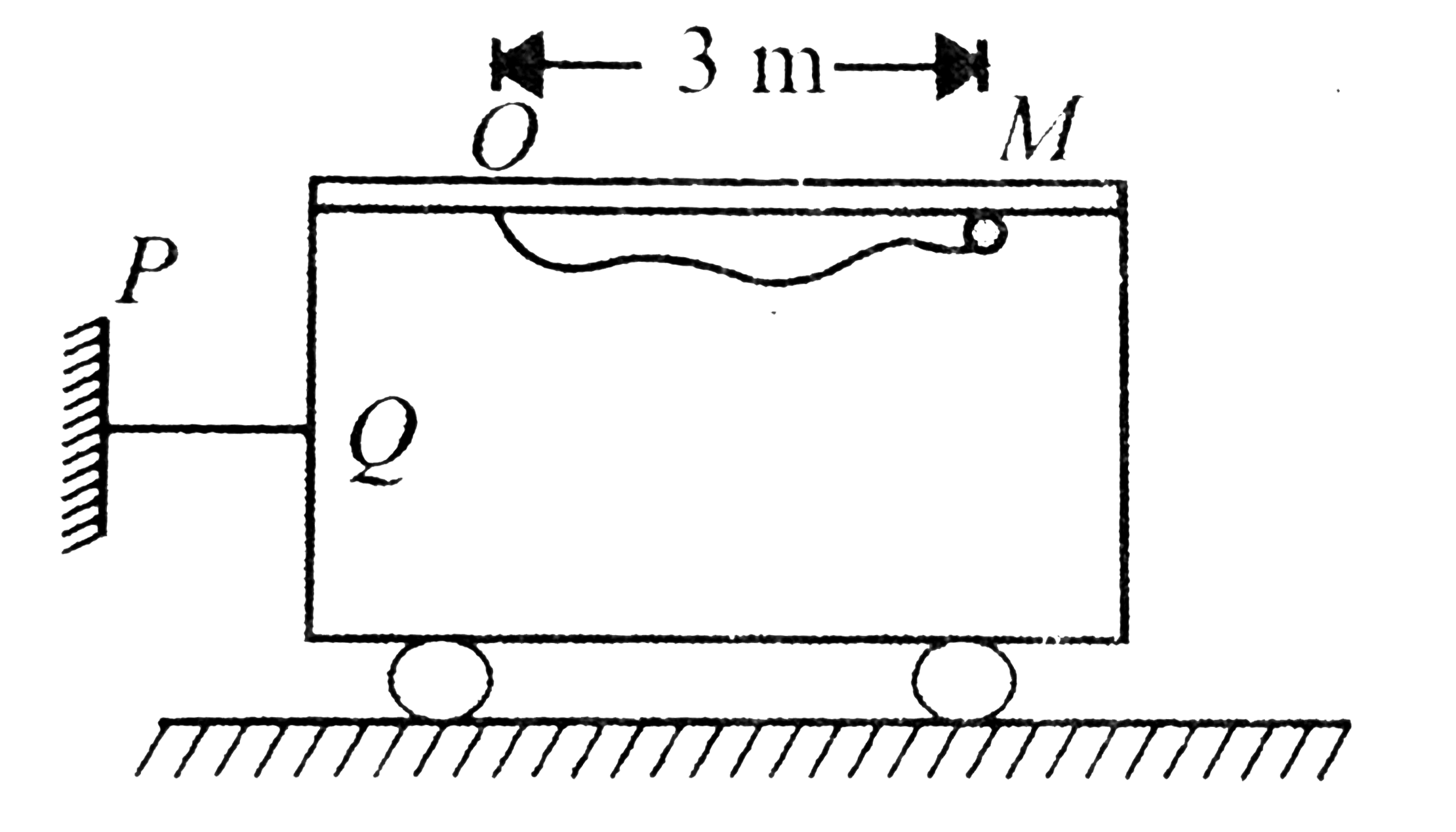
a. the impulse developed in the string when it becorries taut,
b. the velocity of the particle just after the string becomes taut,
c. the impulse developed in this string PQ at this instant.View SolutionA bob of mass m is connected by string of length L to point P. The system is released from rest with the pendulum bob in a horizontal position. Which of the following graph is correctly showing the variation of T (tension) with Ɵ?
View SolutionA small ball of mass 100g is attached to a light and inextensible string of length 50cm. The string is tied to a support O and the mass m released from point A which is a' a horizontal distance of 30cm from the support. Calculate the speed of the ball is its lowest point of the trajectory.
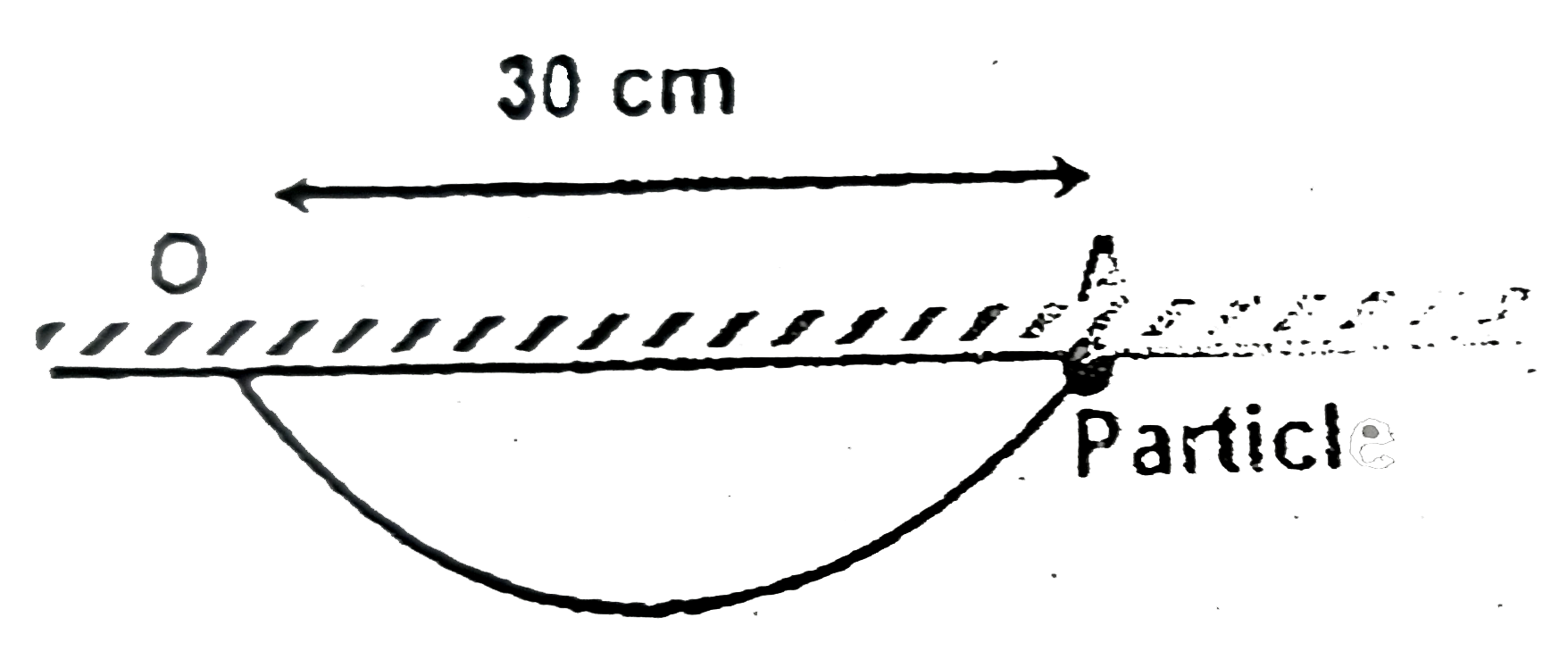 View Solution
View SolutionA particle of mass m attached to the end of string of length l is released from the horizontal position. The particle rotates in a circle about O as shown When it is vertically below O, the string makes contact with a nail N placed directly below O at a distance h and rotates around it. For the particle to swing completely around the nail in a circle.
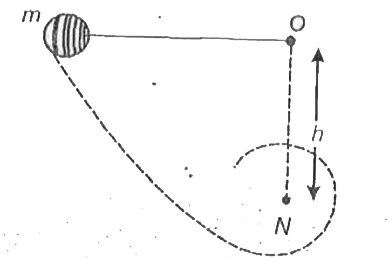 View Solution
View SolutionOne end of string of length 1.5 m is tied to a stone of mass 0.4 kg and the other end to a small pivot on a smooth vertical board. What is the minimum speed of the stone required at its lowermost.point so that the string does not slack at any point in its motion along the vertical circle ?
View SolutionA particle, held by a string whose other end is attached to a fixed point C, moves in a circle on a horizontal frictionless surface. If the string is cut, the angular momentum of the particle about the point C
View SolutionA bob of mass m attached with a string of length l tied to a point on ceiling is released from a position when its string is horizontal. At the bottom most point of its motion, an identical mass m gently stuck to it. Find the maximum angle from the vertical to which it rotates.
View SolutionA particle of mass m, attached to the end of string of length l is released from the initial position A as shown in the figures. The particle moves in a vertical circular path about O. When it is vetically below O, the string makes contact with nail N placed directly below O at distance h and rotat es around it. If the particle just complete the vertical circle about N,then
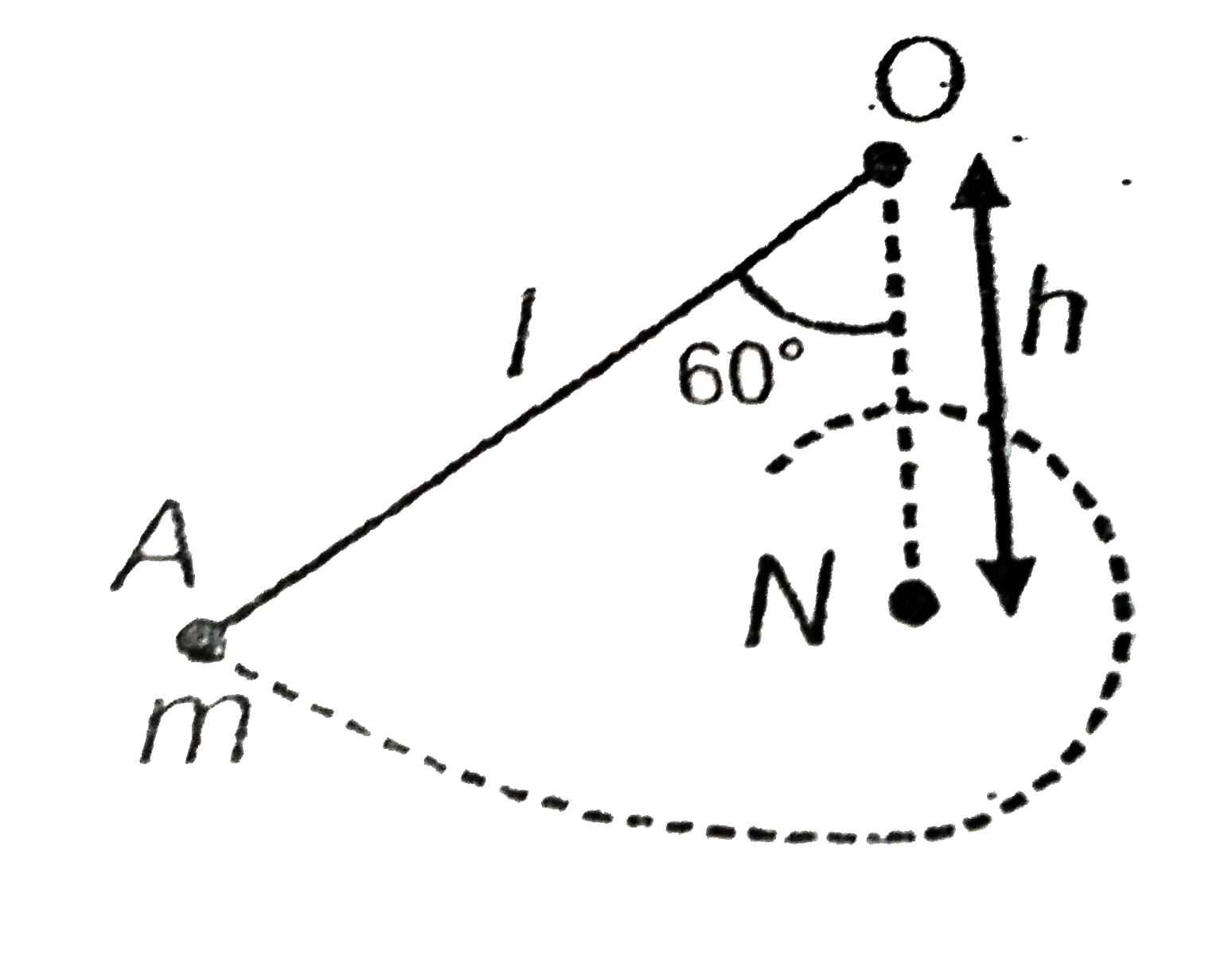 View Solution
View SolutionA particle of mass 'm' is attached to one end of a string of length 'l' while the other end is fixed to a point 'h' above the horizontal table, the particle is made to revolve in a circle on the table, so as to make P revolution per sec. The maximum value of P if the particle is to be contact with the table is
View SolutionA ball of mass m is attached to one end of a light rod of length l, the other end of which is hinged. What minimum velocity v should be imparted to the ball downwards, so that it can complete the circle ?
 View Solution
View Solution

