A stone tied to an inextensible string of length l=1m is kept horizontal. If it is released, find the angular speed of the stone when the string makes an angle θ=30∘ with horizontal.
To find the angular speed of the stone when the string makes an angle of θ=30∘ with the horizontal, we can follow these steps:
Step 1: Understand the Setup
The stone is tied to an inextensible string of length l=1m and is released from a horizontal position. As it falls, it moves in a circular path.
Step 2: Identify Forces Acting on the Stone
When the stone is at an angle θ with the horizontal, two forces act on it:
1. The gravitational force mg acting downwards.
2. The tension in the string acting towards the center of the circular path.
Step 3: Resolve the Gravitational Force
The gravitational force can be resolved into two components:
- A component acting along the direction of motion (tangential): mgsinθ
- A component acting towards the center (centripetal): mgcosθ
Step 4: Apply the Work-Energy Principle
As the stone moves from the horizontal position to the angle θ, it converts potential energy into kinetic energy. The change in potential energy is given by:
ΔPE=mgh=mg(l−lcosθ)=mgl(1−cosθ)
Where h=l(1−cosθ) is the vertical drop.
Step 5: Write the Kinetic Energy
The kinetic energy KE of the stone when it has angular speed ω is given by:
KE=12Iω2
For a point mass, the moment of inertia I about the pivot is ml2:
KE=12ml2ω2
Step 6: Set Up the Energy Equation
Equating the change in potential energy to the kinetic energy gives:
mgl(1−cosθ)=12ml2ω2
Step 7: Simplify the Equation
Cancel m and l (since l=1m):
g(1−cosθ)=12ω2
Rearranging gives:
ω2=2g(1−cosθ)
Step 8: Substitute Values
Substituting g=10m/s2 and θ=30∘:
cos30∘=√32
So,
1−cos30∘=1−√32=2−√32
Thus,
ω2=2⋅10⋅2−√32=10(2−√3)
Step 9: Calculate ω
Taking the square root:
ω=√10(2−√3)
Step 10: Final Calculation
Calculating ω:
ω≈√10(2−0.866)=√10⋅1.134≈√11.34≈3.37rad/s
Final Answer
The angular speed of the stone when the string makes an angle of 30∘ with the horizontal is approximately 3.37rad/s.
---
The stone is tied to an inextensible string of length l=1m and is released from a horizontal position. As it falls, it moves in a circular path.
When the stone is at an angle θ with the horizontal, two forces act on it:
1. The gravitational force mg acting downwards.
2. The tension in the string acting towards the center of the circular path.
The gravitational force can be resolved into two components:
- A component acting along the direction of motion (tangential): mgsinθ
- A component acting towards the center (centripetal): mgcosθ
As the stone moves from the horizontal position to the angle θ, it converts potential energy into kinetic energy. The change in potential energy is given by:
ΔPE=mgh=mg(l−lcosθ)=mgl(1−cosθ)
Where h=l(1−cosθ) is the vertical drop.
The kinetic energy KE of the stone when it has angular speed ω is given by:
KE=12Iω2
For a point mass, the moment of inertia I about the pivot is ml2:
KE=12ml2ω2
Equating the change in potential energy to the kinetic energy gives:
mgl(1−cosθ)=12ml2ω2
Cancel m and l (since l=1m):
g(1−cosθ)=12ω2
Rearranging gives:
ω2=2g(1−cosθ)
Substituting g=10m/s2 and θ=30∘:
cos30∘=√32
So,
1−cos30∘=1−√32=2−√32
Thus,
ω2=2⋅10⋅2−√32=10(2−√3)
Taking the square root:
ω=√10(2−√3)
Calculating ω:
ω≈√10(2−0.866)=√10⋅1.134≈√11.34≈3.37rad/s
The angular speed of the stone when the string makes an angle of 30∘ with the horizontal is approximately 3.37rad/s.
Topper's Solved these Questions
- KINEMATICS-2BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-2EXERCISE - Solved Examples
7 Videos
- KINEMATICS-2BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-2EXERCISE - Exercise 5.1
15 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-1EXERCISE - Integer
9 Videos
- KINETIC THEORY OF GASESBOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASESEXERCISE - Compression
2 Videos
Similar Questions
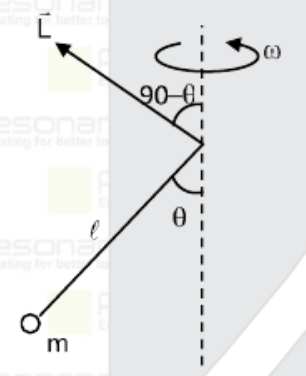
A bob of mass m attached to an inextensible string of length l, is suspended from a vertical support. Bob rotates in a horizontal circle with angular speed ω and string makes an angle of θ with the vertical. Find the angular momentum of bob about axis of rotation
View SolutionIf a simple pendulum of mass m is released from a horizontal position, find the tension in the string as a function of the angle θ with the horizontal.
View Solution
Knowledge Check
A stone tied to a string of length l is whirled in a horizontal circle at a constant angular speed ω in a circle of radius r. If the string makes an angle θ with vertical then the tension in the string is :
Am(gcosθ+ω2r)Bm√ω4r2+g2Cm√ω2r2+g2Dm(gcosθ−ω2r)A heavy particle hanging from a fixed point by a light inextensible string of length l is projected horizontally with speed (gl) . Then the speed of the particle and the inclination of the string to the vertical at the instant of the motion when the tension in the string equal the weight of the particle-
A√31g,cos−1(3/2)B√1g3,cos−1(2/3)C√3g3,cos−1(2/3)D√gl3,cos−1(2/3)A stone of mass m tied to a string of length l is rotated in a circle with the other end of the string as the centre. The speed of the stone is v. If the string breaks, the stone will move
Amove towards the centreBmove away from the centreCmove along a tangentDstop
A coical pendulum consists of a string of length L whose upper end is fixed and another end is tied to a bob. The bob is moving in horizontal circle with constant angular speed ω such that the string makes a constant angle θ with the verticle. calculate time period T0 of revolution of bob in terms of L,g and θ.
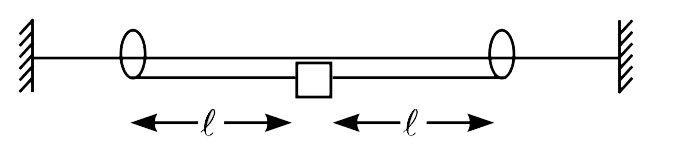
View SolutionTwo small rings each of mass ‘m’ are connected to a block of same mass ‘m’ through inextensible light strings. Rings are constrained to move along a smooth horizontal rod. Initially system is held at rest (as shown in figure) with the strings just taut. Length of each string is ‘l’. The system is released from the position shown. Find the speed of the block (v) and speed of the rings (u) when the strings make an angle of theta=60^(@)withvertical.(Takeg = 10 m//s^2)
View SolutionA stone of mass 100g is suspended from the end of a weightless string of length 100cm and is allowed to swing in a verticle plane The speed of the mass is 200cm−1 when the string makes an angle of 60∘ Also calculate the speed of the stone when it is in the lowest position Given g=980cms−2 .
View SolutionA stone is tied to the end of a string of length 1 and whirled in a horizental circle. When the string breaks then stone
View SolutionA stone of a mass m tied to a string of length /is rotated in a circle with the other end of the string as the centre. The speed of the stone is V. If the string breaks, the stone will
View Solution
