A string 1 has twice the length, twice the radius, twice the tension and twice the density of another string 2. The relation between the fundamental frequency of 1 and 2 is
f1=2f2
f1=4f2
f2=4f1
f1=f2
The correct Answer is:C
To find the relationship between the fundamental frequencies of two strings (string 1 and string 2) given their respective properties, we can follow these steps:
1. Identify the Given Parameters:
- For string 1:
- Length L1=2L2
- Radius R1=2R2
- Tension T1=2T2
- Density ρ1=2ρ2
2. Fundamental Frequency Formula:
The fundamental frequency f of a string is given by the formula:
f=12L√Tμ
where μ (linear mass density) is defined as:
μ=ρ⋅A
and A (cross-sectional area) for a circular string is:
A=πR2
Thus, we can express μ as:
μ=ρ⋅πR2
3. Express the Frequencies:
- For string 1:
f1=12L1√T1μ1=12(2L2)√2T22ρ2⋅π(2R2)2
Simplifying this:
f1=14L2√2T22ρ2⋅π⋅4R22=14L2√T2ρ2⋅πR22
- For string 2:
f2=12L2√T2μ2=12L2√T2ρ2⋅πR22
4. Find the Ratio of Frequencies:
Now, we can find the ratio of the fundamental frequencies:
f1f2=14L2√T2ρ2⋅πR2212L2√T2ρ2⋅πR22
This simplifies to:
f1f2=14⋅2L2L2=12
5. Final Relationship:
Thus, we can conclude that:
f1=12f2
or equivalently:
f2=2f1
Conclusion:
The fundamental frequency of string 2 is twice that of string 1.
- For string 1:
- Length L1=2L2
- Radius R1=2R2
- Tension T1=2T2
- Density ρ1=2ρ2
The fundamental frequency f of a string is given by the formula:
f=12L√Tμ
where μ (linear mass density) is defined as:
μ=ρ⋅A
and A (cross-sectional area) for a circular string is:
A=πR2
Thus, we can express μ as:
μ=ρ⋅πR2
- For string 1:
f1=12L1√T1μ1=12(2L2)√2T22ρ2⋅π(2R2)2
Simplifying this:
f1=14L2√2T22ρ2⋅π⋅4R22=14L2√T2ρ2⋅πR22
f2=12L2√T2μ2=12L2√T2ρ2⋅πR22
Now, we can find the ratio of the fundamental frequencies:
f1f2=14L2√T2ρ2⋅πR2212L2√T2ρ2⋅πR22
This simplifies to:
f1f2=14⋅2L2L2=12
Thus, we can conclude that:
f1=12f2
or equivalently:
f2=2f1
The fundamental frequency of string 2 is twice that of string 1.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - ONLY ONE OPTION IS CORRECT62videos
WAVE MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - More Than One Option is Correct23videos
WAVE MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - Subjective Questions2videos
WAVE MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - VECTORSEXERCISE - Medical enrances gallery9videos
VECTORS
- BOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 Comprehension Based2videos
WORK, ENERGY & POWER
Similar Questions
The length , radius , tension and density of stringA are twice the same parameters of string B. Find the ratio of fundamental frequency of B to the fundamental frequency of A.
View SolutionAn open organ pipe of length 1m contains a gas whose density is twice the density of atmosphere at STP. Find the difference between fundamental and second harmonic frequencies if speed of sound in atmosphere is 300 m/s.
View SolutionThe tension, length, diameter and density of a string B are double than that of another string A. Which of the following overtones of B is same as the fundamental frequency of A?
View SolutionA musical instrument is made using four different metal strings, 1, 2, 3 and 4 with mass per unit length
μ,2μ,3μand4μ respectively. The instrument is played by vibrating the strings by varying the free length in between the range
L0and2L0. It is found that in string-1
(μ) at free length L0 and tension T0 the fundamental mode frequency is f0 .
List-I gives the above four strings while list-II lists the magnitude of some quantity.
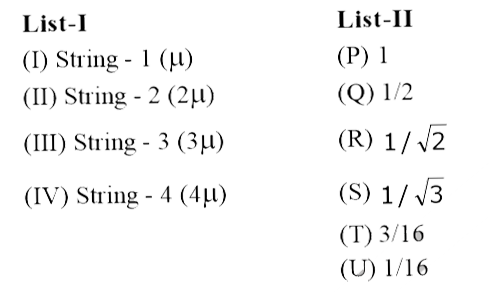
If the tension in each string is T0, the correct match for the highest fundamental frequency in f0 units will be -View SolutionA string is fixed at both ends. The tension in the string and density of the string are accurately known but the length and the radius of cross section of the string are known with some errorl If maximum errors made in the measurements of length and radius are 1% and 0.5% respectively them what is the maximum possible percentage error in the calculation of fundamental frequencyof the that string ?
View SolutionIf v1,v2andv3 are the fundamental frequencies of three segments of stretched string , then the fundamental frequency of the overall string is
View SolutionA piano string 1.5m long is made of steel of density 7.7×103kg/m3andγ=2×1011N/m2. It is maintained at a tension which produces an elastic strain of 1% in the string . What is the fundamental frequency of transverse vibration of the string ?
View SolutionA piano string 1.5m long is made of steel of density 7.7×103kg/m3andγ=2×1011N/m2. It is maintained at a tension which produces an elastic strain of 1% in the string . What is the fundamental frequency of transverse vibration of the string ?
View SolutionIf the length of a stretched string is shortened by 40% and the tension is increased by 44%, then the ratio of the final and initial fundamental frequencies is
View SolutionIf the speed of a transverse wave on a stretched string of length 1 m is 60ms−1, what is the fundamental frequency of vibration ?
View Solution

