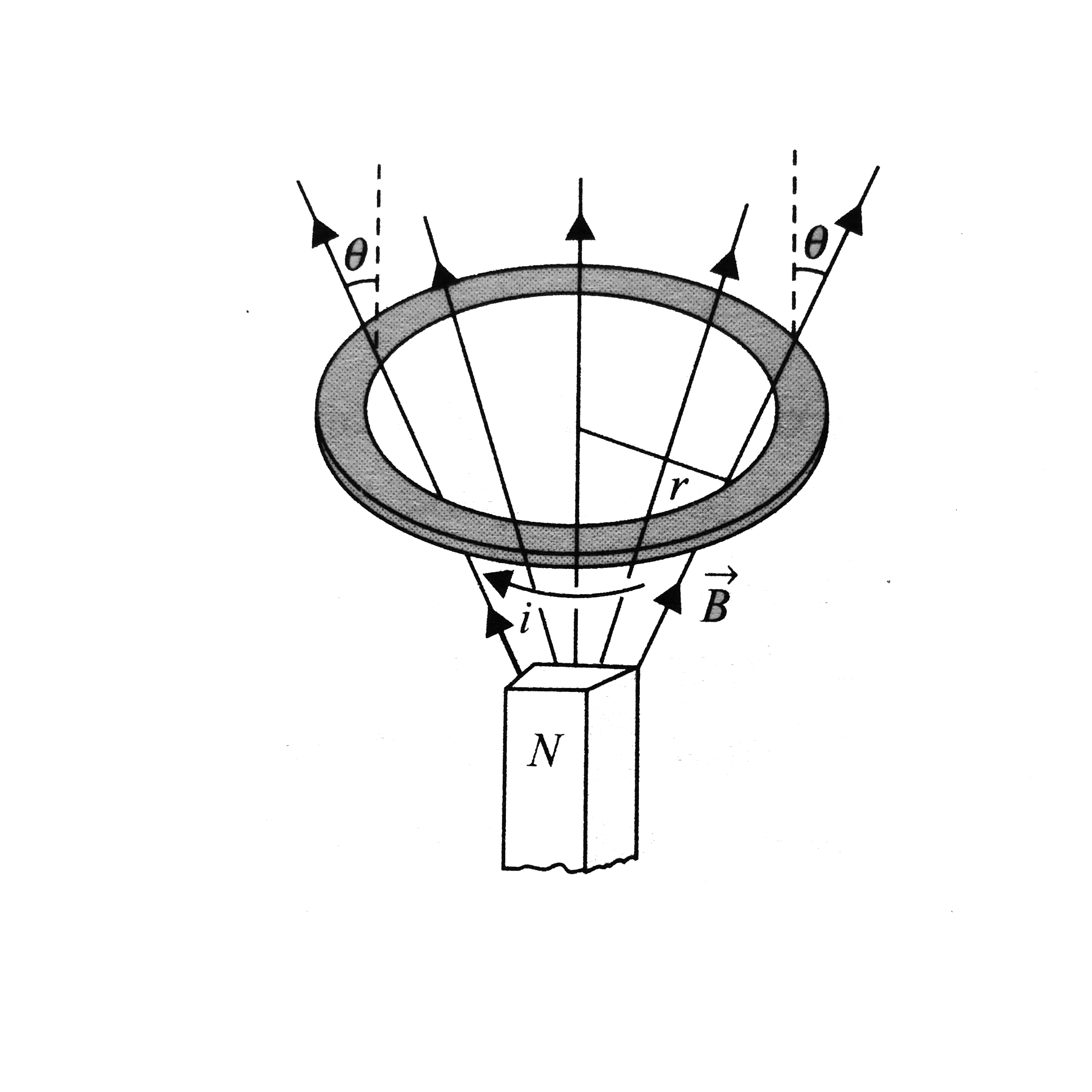
A strong magnet is placed under a horizontal conducting ring of radius r that carries current i as shown in Fig. If the magnetic field makes an angle with the vertical at the ring's location, what are the magnitude and direction of the resultant force on the ring?
The correct Answer is:
The ring carries current and the magnetic field B make an angle
with the vertical at the ring's location.

Consider a small element subtending an angle at the centre of the ring.
Hence, force on the ring due to horizontal component of the field is

Force on the ring due to vertical component of the field is
As the ring lies in a region of constant magnetic field, to it.
The force on it due to this component is zero as
.
Topper's Solved these Questions
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Exercises Single Correct
70 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Exercises Multiple Correct
25 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Exercise1.3
14 Videos
- INDUCTANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Concept Based
8 Videos
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - True and False
3 Videos
Similar Questions
A semicircle conducting ring of radius R is placed in the xy plane, as shown in Fig. A uniform magnetic field is set up along the x-axis. No emf, will be induced in the ring if

View SolutionA conducting ring of radius r having charge q is rotating with angular velocity ω about its axes. Find the magnetic field at the centre of the ring.

View Solution
Knowledge Check
A conducting circular loop of radius r carries a constant current i. It is placed in a uniform magnetic field B such that B is perpendicular to the plane of loop. What is the magnetic force acting on the loop?
AI r BB2πrIBCzeroDπrIB
A conducting ring of radius r having charge q is rotating with angular velocity ω about its axes. Find the magnetic field at the centre of the ring.

View SolutionA conducting ring of radius r and resistance R is placed in region of uniform time varying magnetic field B which is perpendicular to the plane of the ring. It the magnetic field is changing at a rate α, then the current induced in the ring is
View SolutionA thin conducting ring of radius R is given a charge +Q, Fig. The electric field at the center O of the ring due to the charge on the part AKB of the ring is E. The electric field at the center due to the charge on part ACDB of the ring is

View SolutionA battery is connected between two points AandB on the circumference of a uniform conducting ring of radius r and resistance R . One of the arcs AB of the ring subtends an angle θ at the centre . The value of the magnetic induction at the centre due to the current in the ring is
View SolutionThe figure shows a non conducting ring of radius R carrying a charge q. In a circular region of Radius r, a uniform magnetic field B perpendicular to the plane of the ring varies at a constant rate dBdt=β. The torque on the ring is

View SolutionA conducting ring of radius R is being moved in a region of uniform magnetic field as shown. Let EAB represent the potential difference between A and B then
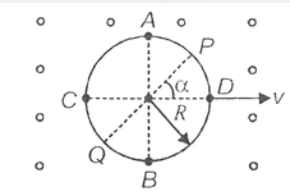
View SolutionA Conducting ring of radius 1 meter is placed in an uniform magnetic field B of 0.01 tesla oscillating with frequency 100Hz with its plane at right angles to B. What will be the induced electric field?
View Solution
