A Conducting ring of radius 1 meter is placed in an uniform magnetic field B of 0.01 tesla oscillating with frequency 100Hz with its plane at right angles to B. What will be the induced electric field?
π volts/m
2 volts/m
10 volts/m
62 volts/m
The correct Answer is:A
To solve the problem of finding the induced electric field in a conducting ring placed in an oscillating magnetic field, we can follow these steps:
1. Identify the Given Values:
- Radius of the conducting ring, r=1 meter
- Magnetic field strength, B=0.01 tesla
- Frequency of oscillation, f=100 Hz
2. Calculate the Area of the Ring:
The area A of the ring can be calculated using the formula for the area of a circle:
A=πr2=π(12)=πm2
3. Determine the Time Period:
The time period T is the reciprocal of the frequency:
T=1f=1100=0.01s
4. Calculate the Change in Magnetic Flux:
The magnetic flux Φ through the ring is given by:
Φ=B⋅A
Since the magnetic field is oscillating, we consider the maximum magnetic flux:
Φmax=B⋅A=0.01⋅π
5. Calculate the Induced EMF:
The induced EMF E can be calculated using Faraday's law of electromagnetic induction:
E=−dΦdt
Since the magnetic field oscillates sinusoidally, the average rate of change of flux over one quarter of the cycle (from 0 to maximum) is:
E=4ΦmaxT=4⋅(0.01⋅π)0.01=4πvolts
6. Relate Induced EMF to Electric Field:
The induced EMF is also related to the electric field E around the ring:
E=E⋅(2πr)
Substituting r=1:
4π=E⋅(2π)
7. Solve for the Electric Field:
Rearranging the equation gives:
E=4π2π=2volts/m
Final Answer:
The induced electric field in the conducting ring is E=2volts/m.
---
- Radius of the conducting ring, r=1 meter
- Magnetic field strength, B=0.01 tesla
- Frequency of oscillation, f=100 Hz
The area A of the ring can be calculated using the formula for the area of a circle:
A=πr2=π(12)=πm2
The time period T is the reciprocal of the frequency:
T=1f=1100=0.01s
The magnetic flux Φ through the ring is given by:
Φ=B⋅A
Since the magnetic field is oscillating, we consider the maximum magnetic flux:
Φmax=B⋅A=0.01⋅π
The induced EMF E can be calculated using Faraday's law of electromagnetic induction:
E=−dΦdt
Since the magnetic field oscillates sinusoidally, the average rate of change of flux over one quarter of the cycle (from 0 to maximum) is:
E=4ΦmaxT=4⋅(0.01⋅π)0.01=4πvolts
The induced EMF is also related to the electric field E around the ring:
E=E⋅(2πr)
Substituting r=1:
4π=E⋅(2π)
Rearranging the equation gives:
E=4π2π=2volts/m
The induced electric field in the conducting ring is E=2volts/m.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTION & ALTERNATIVE CURRENT Book:VMC MODULES ENGLISHChapter:ELECTROMAGNETIC INDUCTION & ALTERNATIVE CURRENT Exercise:IMPECCABLE
Explore 52 Videos
- ELECTROMAGNETIC INDUCTION & ALTERNATIVE CURRENT Book:VMC MODULES ENGLISHChapter:ELECTROMAGNETIC INDUCTION & ALTERNATIVE CURRENT Exercise:ENABLE
Explore 50 Videos
- ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTBook:VMC MODULES ENGLISHChapter:ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTExercise:IN-CHAPTER EXERCISE-G
Explore 10 Videos
- ELECTROSTATICSBook:VMC MODULES ENGLISHChapter:ELECTROSTATICSExercise:JEE Advanced (Archive)
Explore 89 Videos
Similar Questions
A conducting disc of radius R is placed in a uniform and constant magnetic field B parallel to the axis of the disc.With what angular speed should the disc be rotated about its axis such that no electric field develops in the disc (the electric charge and mass are e and m)
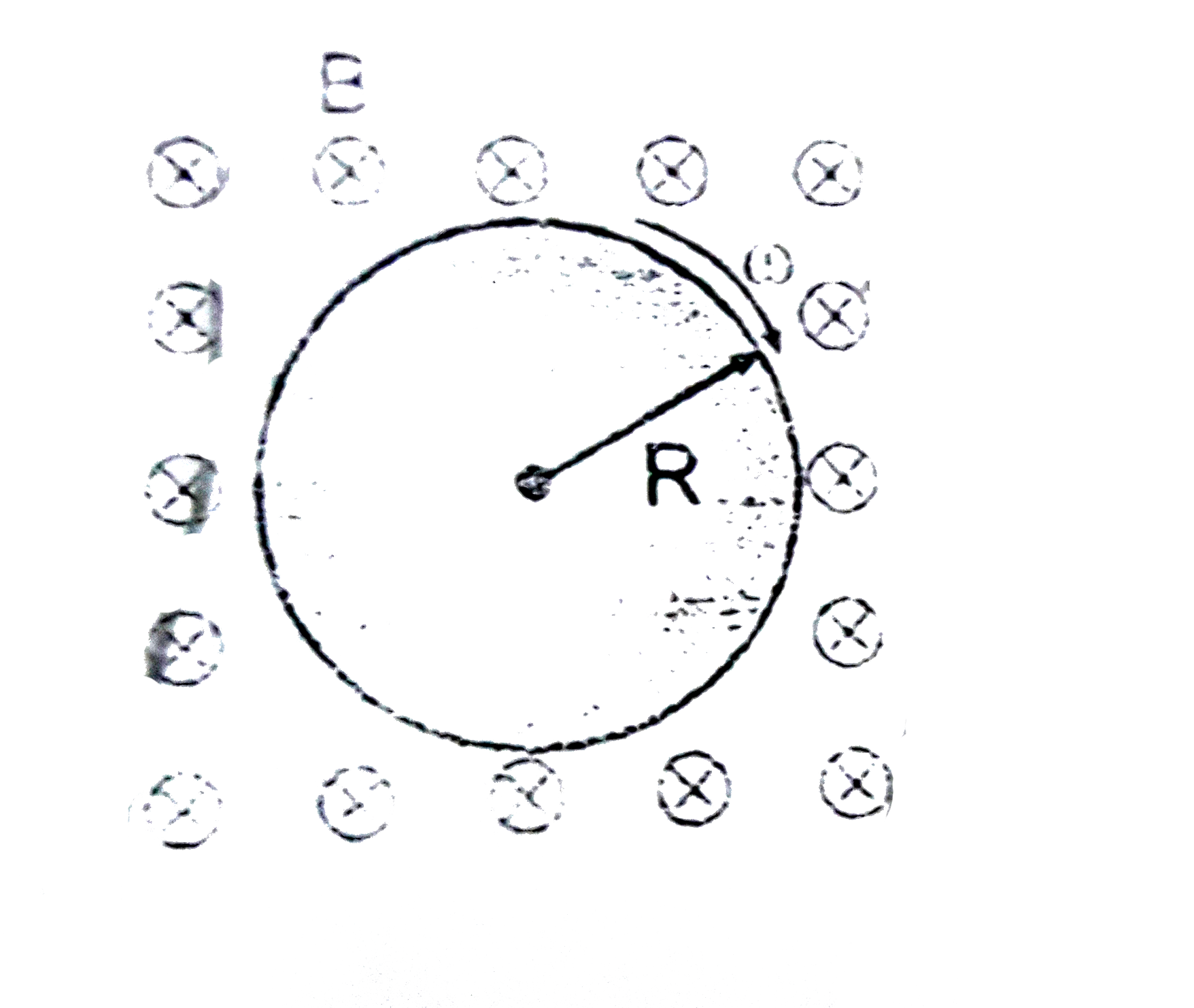
View SolutionA conducting ring of radius R is being moved in a region of uniform magnetic field as shown. Let EAB represent the potential difference between A and B then
View Solution
Knowledge Check
A conducting ring is placed in a uniform magnetic field with its plane perpendicular to the field . An emf is induced in the ring if
Ait is rotated about its axis.Bit is rotated about its diameter.Cit is not moved.Dit is given translational motion in the field.A conducting circular loop of radius r carries a constant current i. It is placed in a uniform magnetic field B such that B is perpendicular to the plane of loop. What is the magnetic force acting on the loop?
AI r BB2πrIBCzeroDπrIBA conducting circular loop is placed in a uniform magnetic field, B=0.025T with its plane perpendicular to the loop. The radius of the loop is made to shrink at a constant rate of 1mms−1. The induced emf when the radius is 2cm is
A2πμVBπμVCπ2μVD2μV
A metal ring of radius r=0.5m with its plane normal a unifrom magnetic field B of induction 0.2T carries a current I=100A The tension in newtons developed in the ring is
View SolutionA semi circular current loop is placed in an uniform magnetic field of 1 tesla as shown. If the radius of loop is 1 m, the magnetic force on the loop is
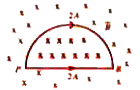
View SolutionA conducting ring of radius r and resistance R is placed in region of uniform time varying magnetic field B which is perpendicular to the plane of the ring. It the magnetic field is changing at a rate α, then the current induced in the ring is
View SolutionA conducting loop of radius R is present in a uniform magnetic field B perpendicular to the plane of the ring. If radius R varies as a function of time t, as R=R0+t. The emf induced in the loop is

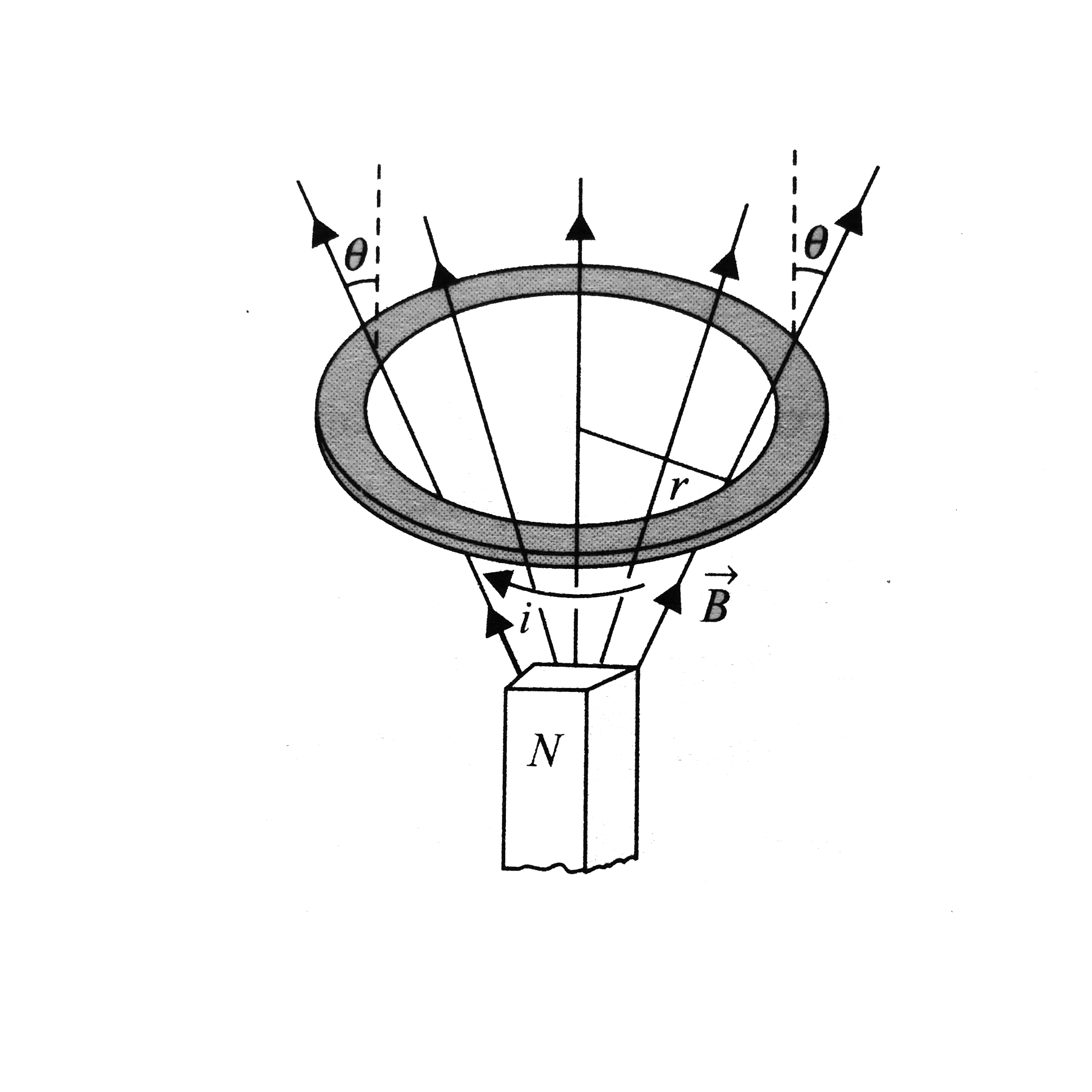
View SolutionA strong magnet is placed under a horizontal conducting ring of radius r that carries current i as shown in Fig. If the magnetic field makes an angle θ with the vertical at the ring's location, what are the magnitude and direction of the resultant force on the ring?
View Solution
