A student forgot Newton's formula for speed of sound but the knows there speed (v), pressure (p) and density (d) in the formula. He then start using dimensional analysis method to find the actual relation.
υ=kpxdy
Where k is a dimensionless constant. On the basis of above passage answer the following questions:
The value of x is :
1
12
−12
2
The correct Answer is:B
Step by step video, text & image solution for A student forgot Newton's formula for speed of sound but the knows there speed (v), pressure (p) and density (d) in the formula. He then start using dimensional analysis method to find the actual relation. upsilon = kp^(x)d^(y) Where k is a dimensionless constant. On the basis of above passage answer the following questions: The value of x is : by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - ANURAG MISHRACHAPTER - UNIT AND DIMENSIONSEXERCISE - Passage 21videos
UNIT AND DIMENSIONS
- BOOK - ANURAG MISHRACHAPTER - UNIT AND DIMENSIONSEXERCISE - Passage 31videos
UNIT AND DIMENSIONS
- BOOK - ANURAG MISHRACHAPTER - UNIT AND DIMENSIONSEXERCISE - More than One Alternatives are Correct5videos
UNIT AND DIMENSIONS
- BOOK - ANURAG MISHRACHAPTER - RIGID BODY MOTIONEXERCISE - MATCH THE COLUMN12videos
RIGID BODY MOTION
- BOOK - ANURAG MISHRACHAPTER - WORK AND ENERGYEXERCISE - Matching types problems14videos
WORK AND ENERGY
Similar Questions
The Casimir effect describes the attraction between two unchanged conducting plates placed parallel to each other in vacuum. The astonishing force ( predicted in 1948 by Hendrik Casimir) per unit area of each plate depends on the planck’s constant (h), speed of light (c) and separation between the plates (r).
(a) Using dimensional analysis prove that the formula for the Casimir force per unit area on the plates is given by F=khcr4 where k is a dimensionless constant
(b) If the force acting on 1×1 cm plates separated by 1μm is 0.013 dyne, calculate the value of constant k.View SolutionThe corrected Newton's formula for velocity of sound in air is v=√γPρ, where P is pressure and ρ is density of air, γ=1.42 for air. At normal temperature ane pressure, velocity of sound in air =332m/s.
Read the above passage and answer the following question:
(i) How do the sound horns protect us from the oncoming vehicles ? ltbr> (ii) How does a sand scorpion fing its prey?
(iii) Will the velocity of sound in air change on changing the pressure alone?View Solution
Knowledge Check
- Question 1 - Select One
A student forgot Newton's formula for speed of sound but the knows there speed (v), pressure (p) and density (d) in the formula. He then start using dimensional analysis method to find the actual relation.
υ=kpxdy
Where k is a dimensionless constant. On the basis of above passage answer the following questions:
If the density will increase the speed of sound will :AincreaseBdecreaseCunchangedDnone of these - Question 2 - Select One
The speed (v) of sound in a gas is given by v=kPxρy
Where K is dimensionless constant, P is pressure, and ρ is the density, thenAx=½,y=½Bx=–½,y=–½Cx=½,y=–½Dx=–½,y=½ - Question 3 - Select One
The velocity of sound in air (V) pressure (P) and density of air (d) are related as Vαpxdy. The values of x and y respectively are
A1,12B−12,−12C12,12D12,−12
A locus is the curve traced out by a point which moves under certain geomatrical conditions: To find the locus of a point first we assume the co-ordinates of the moving point as (h,k) and then try to find a relation between h and k with the help of the given conditions of the problem. If there is any variable involved in the process then we eliminate them. At last we replace h by x and k by y and get the locus of the point which will be an equation in x and y. On the basis of above information, answer the following questions Locus of centroid of the triangle whose vertices are (acost,asint),(bsint,−bcost)and(1,0) where t is a parameter is -
View SolutionThe velocity of sound in air (V) pressure (P) and density of air (d) are related as Vαpxdy. The values of x and y respectively are
View SolutionIn a problem of differentiation of f(x)g(x), one student writes the derivative of f(x)g(x) as f'(x)g'(x) and he finds the correct result . If g(x)=x2andlimx→∞f(x)=4 On the basis of above information , answer the following questions :
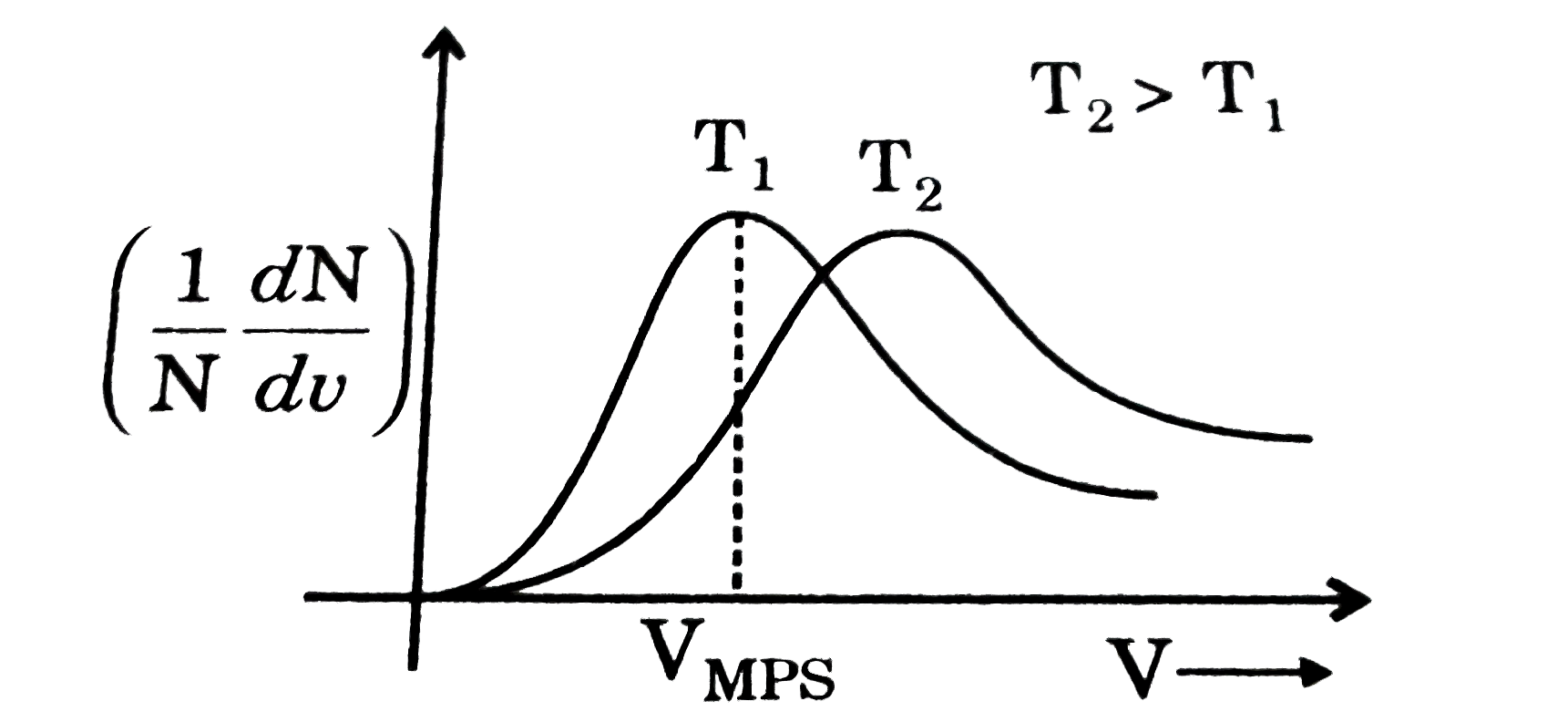
The function f(x) isView SolutionThe speed of a molecule of a gas changes continuously as a result of collisions with other molecules and with the walls of the container. The speeds of individual molecules therefore change with time.
A direct consequence of the distribution of speeds is that the average kinetric energy is constant for a given temperature.
The average K.E. is defined as
¯¯¯¯¯¯KE=1N(12mΣidNiu21)=12m(ΣidNiN.u21)
where dNN is the fraction of molecules having speeds between ui and ui+du and as proposed by maxwell dNN=4π(m2πKT)3/2exp(−mu22KT).u2.du
The plot of (1NdNdu) is plotted for a particular gas at two different temperature against u as shown.
The majority of molecules have speeds which cluster around vMPS in the middle of the range of v. There area under the curve between any two speeds V1andV2 is the fraction of molecules having speeds betweenV1andV2.
The speed distribution also depends on the mass of the molecules. As the area under the curve is the same (equal to unity) for all gas samples, samples which have the same VMPS will have identical Maxwellian plots. On the basis of the above passage answer the questions that follow.
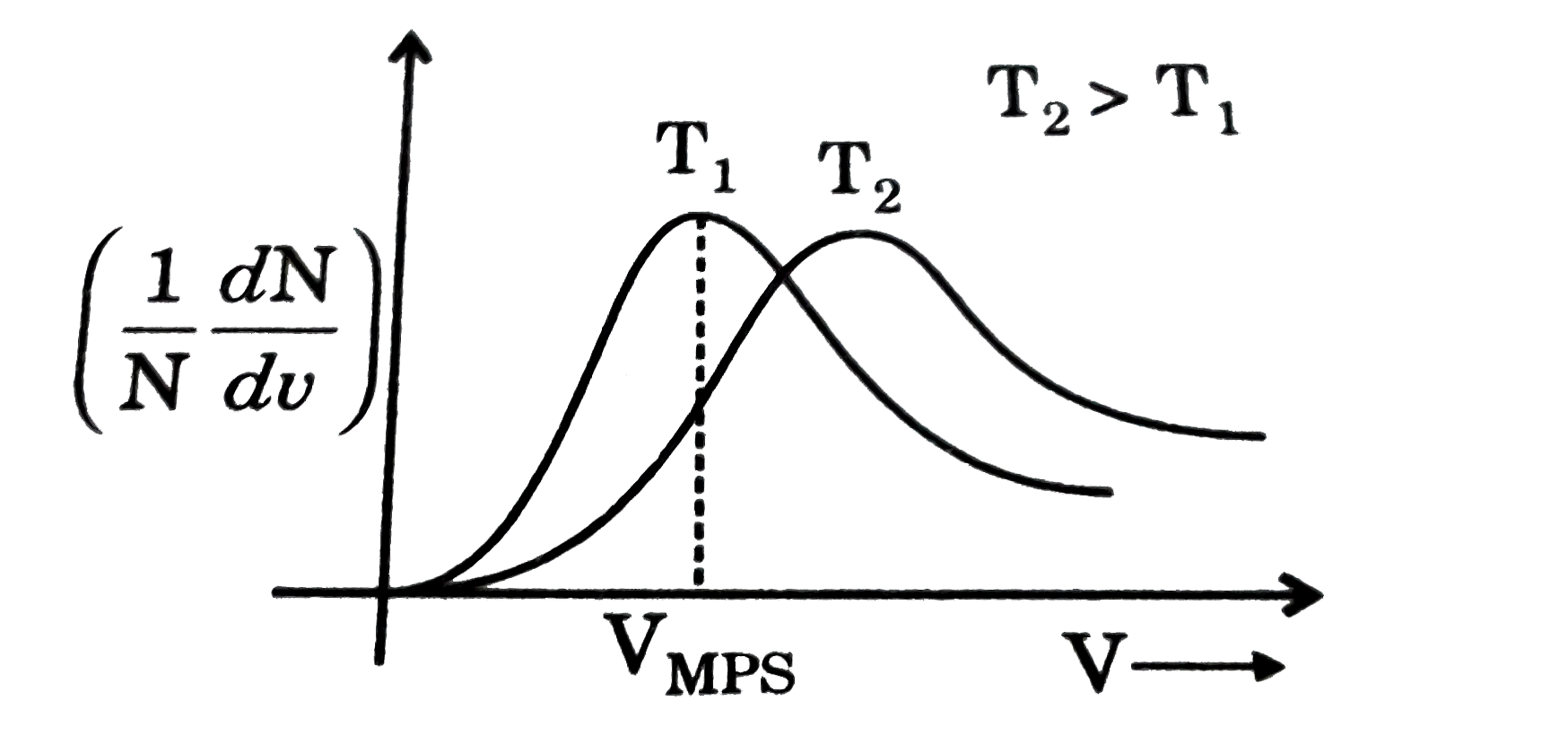
For the above graph, drawn for two different samples of gases at two different temperature T1andT2. Which of the following statements is necessarily true?View SolutionThe speed of a molecule of a gas changes continuously as a result of collisions with other molecules and with the walls of the container. The speeds of individual molecules therefore change with time.
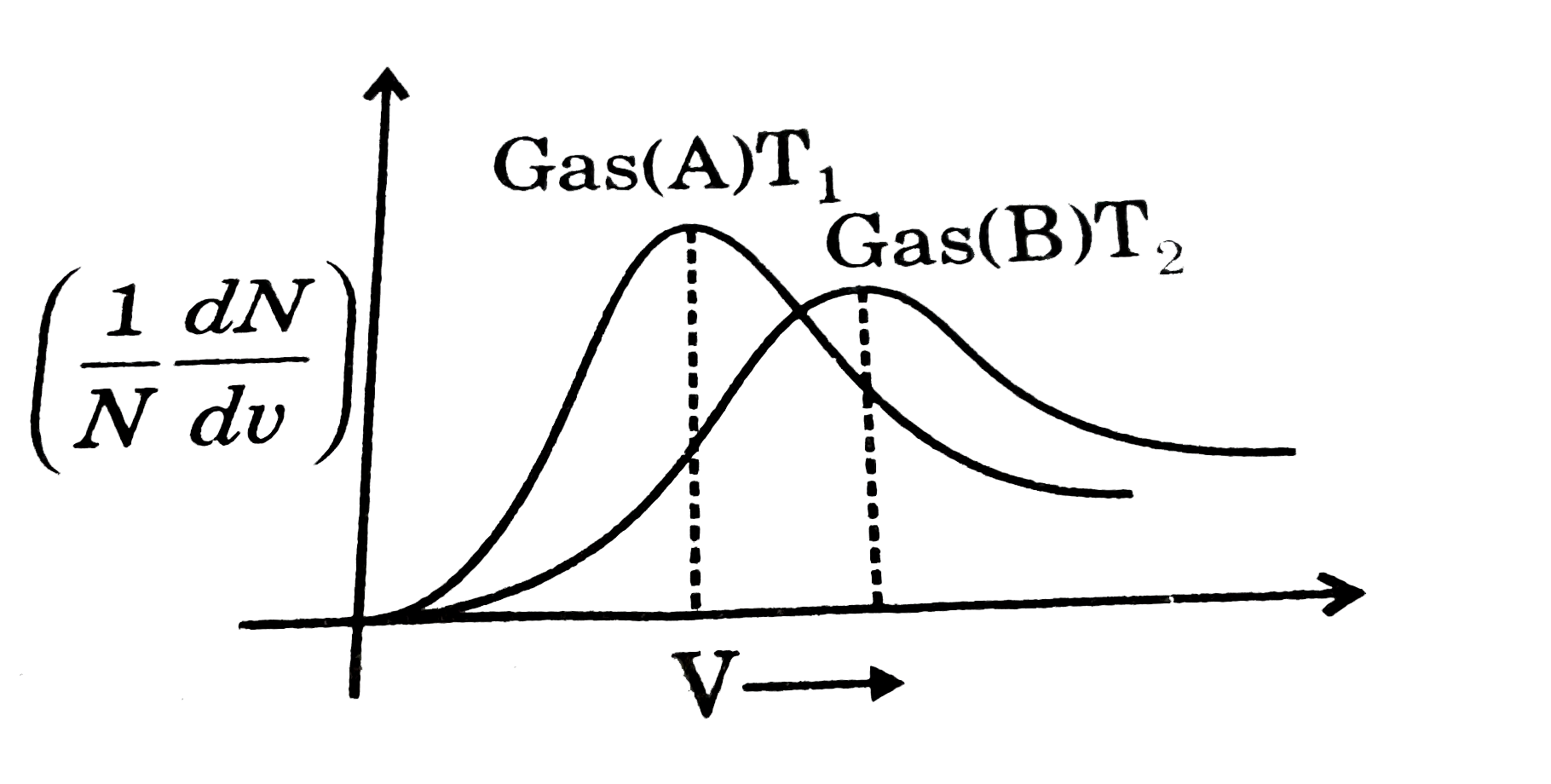
A direct consequence of the distribution of speeds is that the average kinetric energy is constant for a given temperature.
The average K.E. is defined as
¯¯¯¯¯¯KE=1N(12mΣidNiu21)=12m(ΣidNiN.u21)
where dNN is the fraction of molecules having speeds between ui and ui+du and as proposed by maxwell dNN=4π(m2πKT)3/2exp(−mu22KT).u2.du
The plot of (1NdNdu) is plotted for a particular gas at two different temperature against u as shown.
The majority of molecules have speeds which cluster around vMPS in the middle of the range of v. There area under the curve between any two speeds V1andV2 is the fraction of molecules having speeds betweenV1andV2.
The speed distribution also depends on the mass of the molecules. As the area under the curve is the same (equal to unity) for all gas samples, samples which have the same VMPS will have identical Maxwellian plots. On the basis of the above passage answer the questions that follow.
If two gases A and B and at temperature TAandTB respectivley have identical Maxwellian plots then which of the following statement are true?View Solution

