The Casimir effect describes the attraction between two unchanged conducting plates placed parallel to each other in vacuum. The astonishing force ( predicted in 1948 by Hendrik Casimir) per unit area of each plate depends on the planck’s constant (h), speed of light (c) and separation between the plates (r).
(a) Using dimensional analysis prove that the formula for the Casimir force per unit area on the plates is given by where k is a dimensionless constant
(b) If the force acting on cm plates separated by is 0.013 dyne, calculate the value of constant k.
The correct Answer is:(b)
Step by step video, text & image solution for The Casimir effect describes the attraction between two unchanged conducting plates placed parallel to each other in vacuum. The astonishing force ( predicted in 1948 by Hendrik Casimir) per unit area of each plate depends on the planck’s constant (h), speed of light (c) and separation between the plates (r). (a) Using dimensional analysis prove that the formula for the Casimir force per unit area on the plates is given by F= k (hc)/(r^(4)) where k is a dimensionless constant (b) If the force acting on 1xx1 cm plates separated by 1 mu m is 0.013 dyne, calculate the value of constant k. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One

Force acting per unit area of each plateA12μ0j2BzeroCm0jD2m0 - Question 2 - Select One
Force of attraction between the plates of a parallel plate capacitor is
Aq22ε0AKBq2ε0AKCq2ε0ADq22ε0A2K - Question 3 - Select One
The capacitance of a capacitor depends on
(A) Charge on the plates
(B) the size of the plates
(C) the shape of the plates
(D) the separation between the platesAA,B,CBA,C,DCB,C,DDA,B,D
Find the equivalent capacitance between A and B.A: area of each plate, d: separation between the plates.
 View Solution
View SolutionFind the equivalent capacitance between A and B.A: area of each plate, d: separation between the plates.
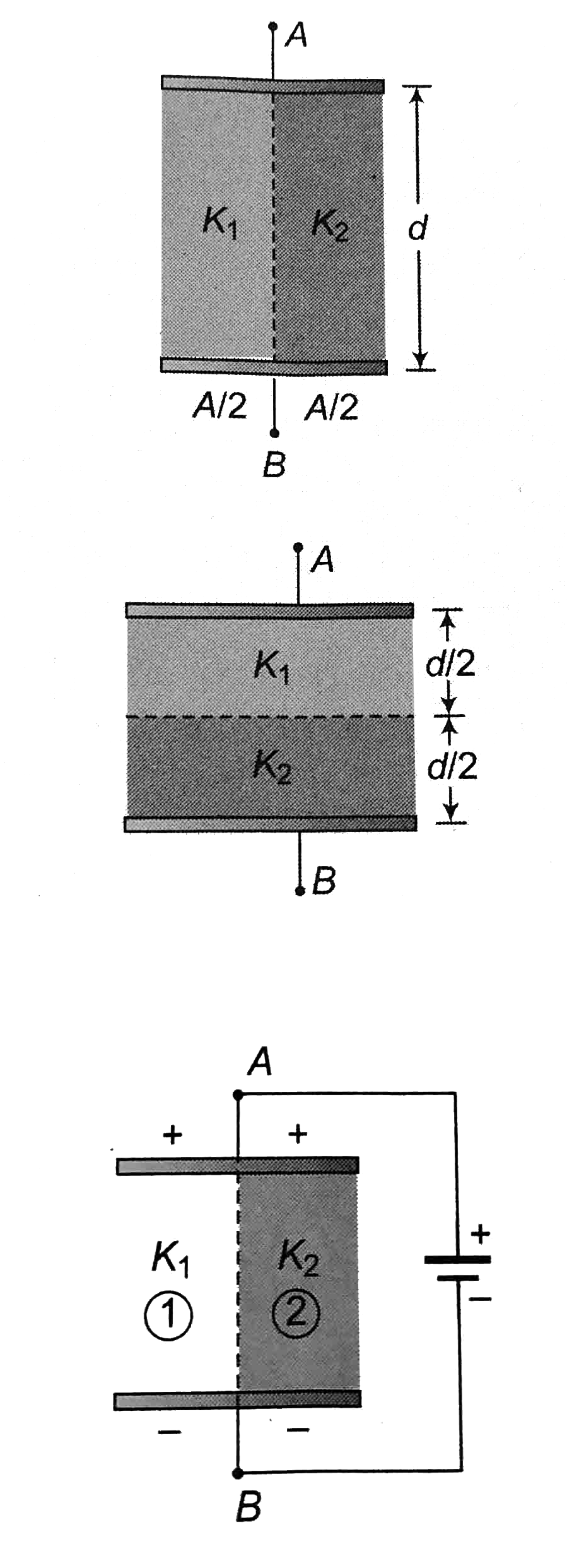 View Solution
View SolutionThe separation between the plates of a charged parallel-plate capacitor is increased. The force between the plates
View SolutionThe electrostatic force between the metal plate of an isolated parallel plate capacitro C having charge Q and area A, is
View SolutionIf the separation between the plates of a capacitor is 5 mm , then area of the plate of a 3 F parallel plate capacitor is
View Solution


