A sufficiently long plane of mass is placed on a smooth horizontal surfaces A small block of mass is placed over the plank and is beging acted upon by a time verying horizontal force where F is in newton and t is in second as shown in figure. The coefficient of friction slipping the plank and the block is given is time the relative slipping between the plank and the block is just likely to accor

The coefficient of friction is equal to
The correct Answer is:c
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer
6 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - True And False
4 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Multiple Correct
2 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Integer
5 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICSCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE
2 Videos
Similar Questions
On a smooth horizontal surface a block A of mass 10kg is kept. On this block a second block B of mass 5kg is kept. The coefficient of friction between the two blocks is 0.4 .A horizontal force of 30N is applied on the lower block as shown. The force of friction between the blocks is
View SolutionSuppose a block of mass 1kg is placed over a rought surface and a horizontal force F is applied on the block as shown in figure. Now let as see what are the values of force of friction f and acceleration of the block a if the force F is gradually increased. Given that μs=0.5,μk=0.4andg=10m/s2

View Solution
Knowledge Check
A sufficiently long plane of mass 4kg is placed on a smooth horizontal surfaces A small block of mass 2kg is placed over the plank and is beging acted upon by a time verying horizontal force F=(0.5t) where f is in newton and t is in second as shown in figure .The coefficient of friction slipping the plank and the block is given is μs=μk=μ time t=12s the relative slipping between the plank and the block is just likely to accor

The average acceleration of the plank in the time interval 0→15s in the figure will beA0.20ms−2B0.30ms−2C0.40ms−2D0.60ms−2A sufficiently long plane of mass 4kg is placed on a smooth horizontal surfaces A small block of mass 2kg is placed over the plank and is beging acted upon by a time verying horizontal force F=(0.5t) where f is in newton and t is in second as shown in figure .The coefficient of friction slipping the plank and the block is given is μs=μk=mu time t=12s the relative slipping between the plank and the block is just likely to accor

The acceleration a versus time l graph for the and the block shown in figure below is correctely represented inA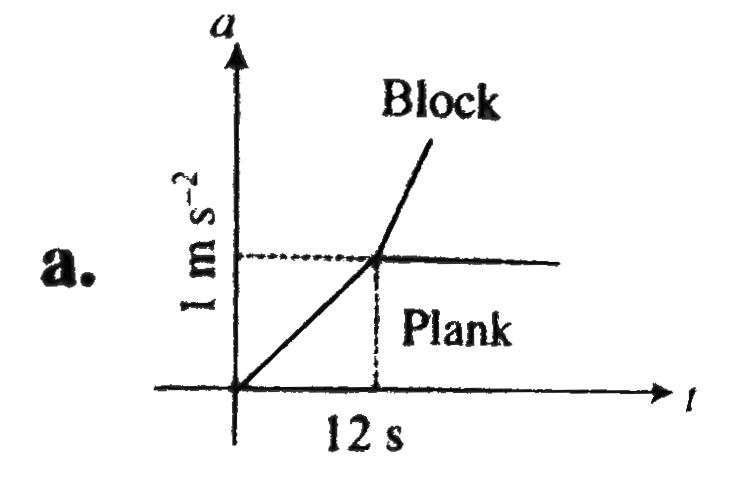 B
B C
C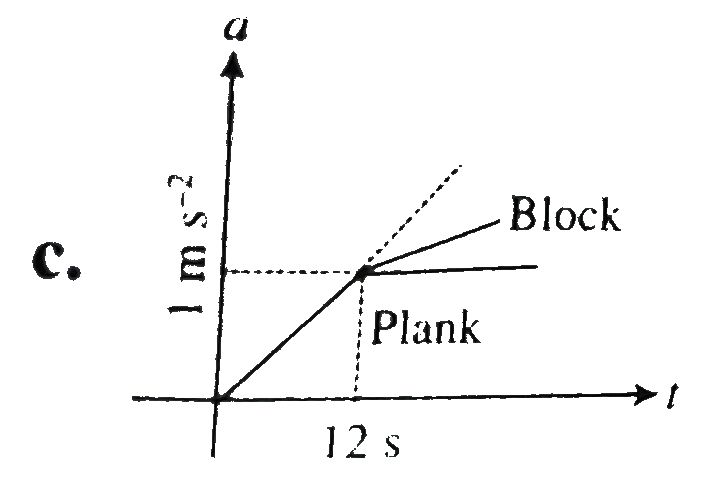 D
D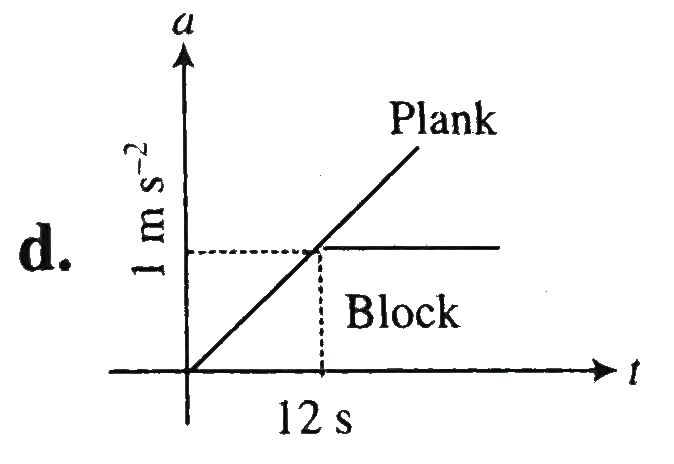
A plank of mass M is placed on a rough horizontal surface. A man m walks on the plank with an acceleration 'a' while the plank is also acted upon by a horizontal force F whose magnitude and direction can be adjusted to keep the plank at rest.
The coefficient of friction between plank and surface is μ. Choose the correct options.
 .AThe maximum value of F to keep plank at rest is ma+μ(M+m)gBThe minimum value of F to keep the plank at rest is ma−μ(M+m)gCThe direction of friction on ground due to plank will always be forwardDIf F=ma then friction on man due to plank is also F and friction between plank and ground will be zero
.AThe maximum value of F to keep plank at rest is ma+μ(M+m)gBThe minimum value of F to keep the plank at rest is ma−μ(M+m)gCThe direction of friction on ground due to plank will always be forwardDIf F=ma then friction on man due to plank is also F and friction between plank and ground will be zero
A plank of mass 10kg rests on a smooth horizontal surface. Two blocks A and B of masses mA=2kgandmB=1kg lies at a distance of 3m on the plank as shown in the distance of 3m on the plank as shown in the figure. The friction coefficient between the blocks and plank are μA=0.3andμB=0.1. Now a force F = 15 N is applied to the plank in horizontal direction. Find the time after which block A collides with B.
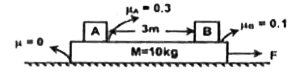
View SolutionA long block A is at rest on a smooth horizontal surface. A small block B whose mass is half of mass of A is placed on A at one end and is given an initial velocity u as shown in figure. The coefficient of friction between the blocks is μ.
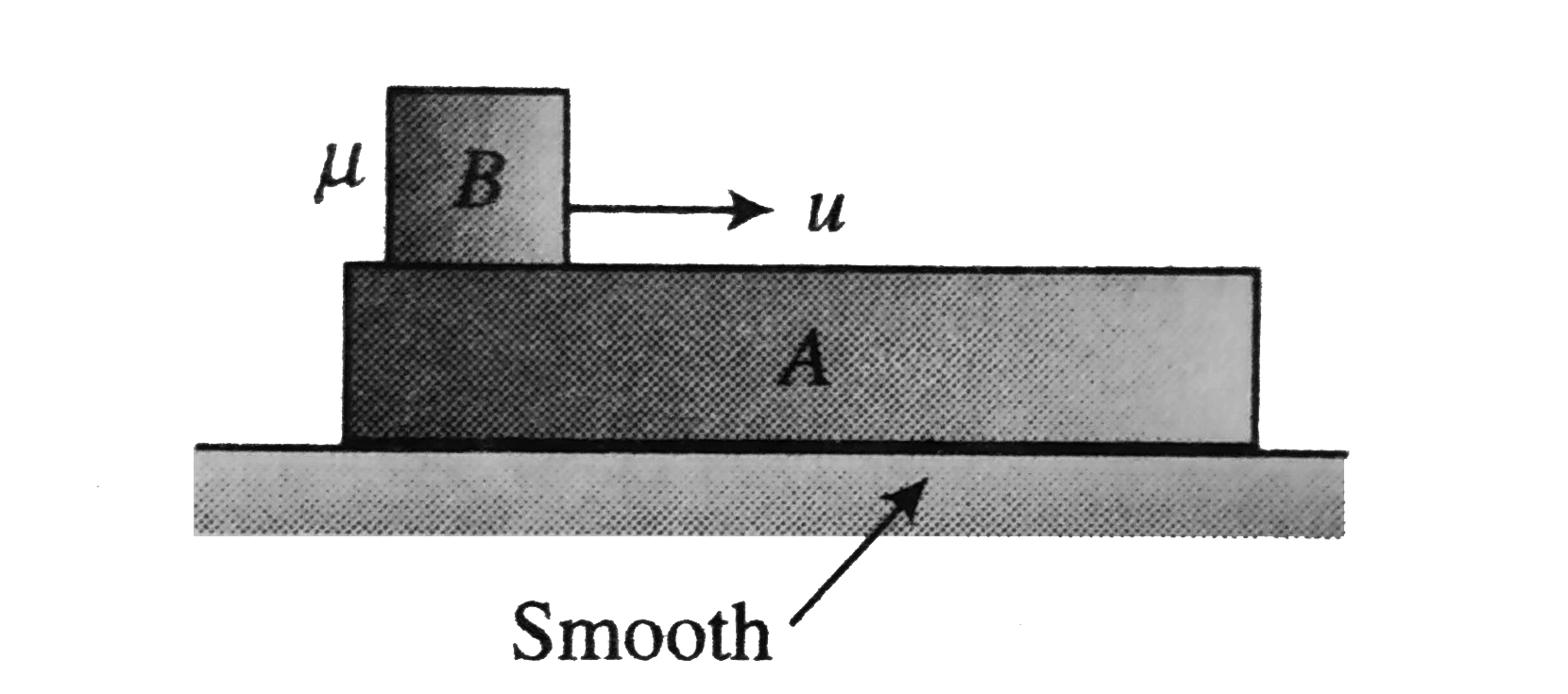
View SolutionA block of mass m is on the smooth horizontal surface of a plank of mass M The plank is on smooth horizontal surface Now, a constant horizontal force F acts on M. Now, for a person standing on the ground:

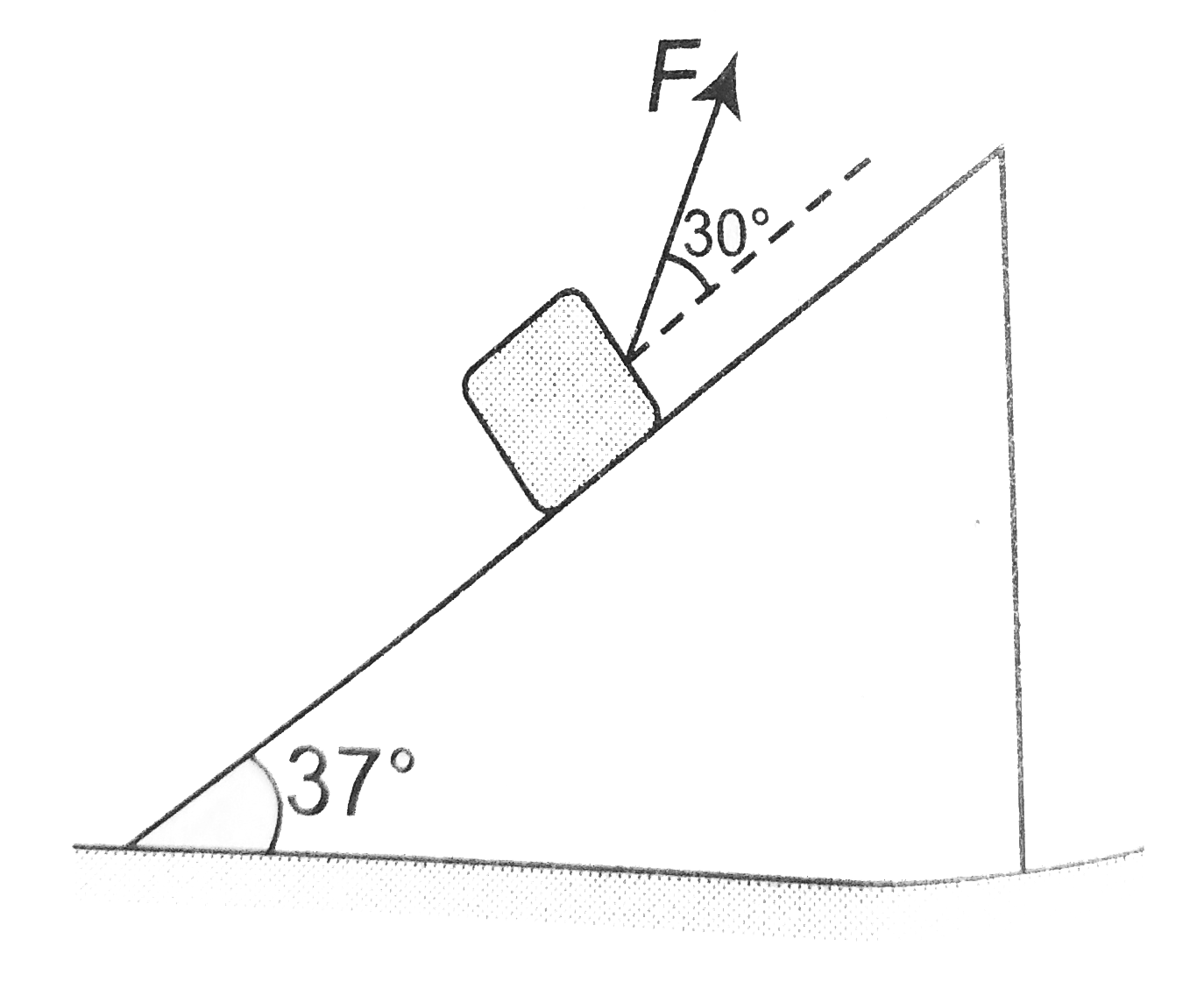
View SolutionA block of mass m=4kg is placed oner a rough inclined plane as shown in figure. The coefficient of friction between the block and the plane is μ=0.5 . A force F=10N is applied on the block at an angle of 30∘ .
View SolutionA block of mass 3kg is placed on a rough horizontal surface (μs=0.4) . A force of 8.7N is applied on the block. The force of friction between the block and floor is .
View Solution
