A system consists of three masses m1 , m1 , m1 , m2 and m3 connected by a string passing over a pulley P . The mass m1 hangs freely and m2 and m3 are on a rough horizontal table (the coefficient of friction=mu) The pulley is frictionless and of negligible mass. The downward acceleration of m1 is (Assume m1=m2=m3=m).

g(1−3μ)9m
2gμ3
g(1−2μ)3
g(1−2μ)2
The correct Answer is:c
Let a be the downward acceleration of mass m pulling force on all the three masses
F=(m1+m2+m3)a
force of friction on masses m2 and m3
f=μ(m2+m3)g
Equation of motion of mass m1 is
(m1+m2+m3)a=m1g−μ(m2+m3)g
or (m+m+m)a=mg−μ(m+m)g
or a=mg(1−2μ)3m=g(1−2μ)3 .
Topper's Solved these Questions
- LAWS OF MOTIONBook:PRADEEPChapter:LAWS OF MOTIONExercise:Integer Type Questions
Explore 7 Videos
- LAWS OF MOTIONBook:PRADEEPChapter:LAWS OF MOTIONExercise:Assertion- Reason Type Questions
Explore 17 Videos
- LAWS OF MOTIONBook:PRADEEPChapter:LAWS OF MOTIONExercise:Problems for practice
Explore 112 Videos
- KINEMATICSBook:PRADEEPChapter:KINEMATICSExercise:1 NCERT Comprehension
Explore 4 Videos
- MATHEMATICAL TOOLSBook:PRADEEPChapter:MATHEMATICAL TOOLSExercise:Fill in the blanks
Explore 5 Videos
Similar Questions
Two blocks of masses m1andm2(m1>m2) connected by a massless string passing over a frictionless pulley Magnitude of acceleration of blocks would be
View SolutionThree masses m1,m2andm3 are attached to a string -pulley system as shown . All the three masses are held at rest and then released If m3 remains at rest , then
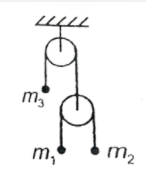
View Solution
Knowledge Check
A system consists of three masses m1 , m1 , m1 , m2 and m3 connected by a string passing over a pulley P . The mass m1 hangs freely and m2 and m3 are on a rough horizontal table (the coefficient of friction=μ) The pulley is frictionless and of negligible mass. The (Assume m1=m2=m3=m).
 Ag(1−2μ)9B2gμ3Cg(1−2μ)3Dg(1−2μ)2
Ag(1−2μ)9B2gμ3Cg(1−2μ)3Dg(1−2μ)2A system consists of three masses m1,m2 and m3 connected by a string passing over a pulley P. The mass m1 hangs freely and m2 and m3 are on a rough horizontal table (the coefficient of friction=μ). The pulley is frictionless and of negligible mass. The downward acceleration of mass m1 is (assume, m1=m2=m3=m)
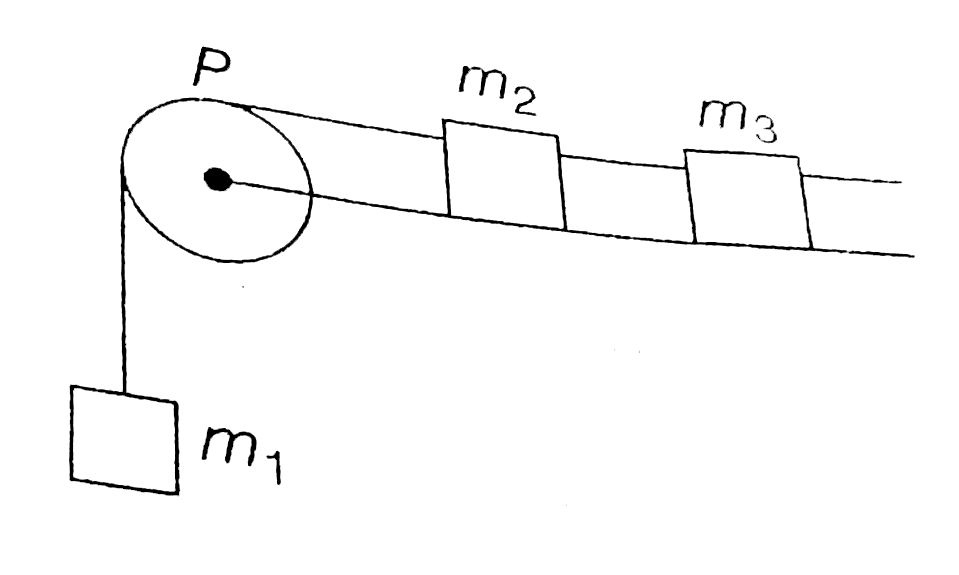 Ag(1−gμ)9B2gμ3Cg(1−2μ)3Dg(1−2μ)2
Ag(1−gμ)9B2gμ3Cg(1−2μ)3Dg(1−2μ)2Two masses m1 and m2 are connected by a light string passing over a smooth pulley. When set free m1 moves downward by 2 m in 2 s. The ratio m1/m2 is
A9/7B11/9C13/11D15/13
Three blocks of masses m1,m2andm3 are connected as shown in the figure. All the surfaces are frictionless and the string and the pulleys are light. Find the acceleration of m1
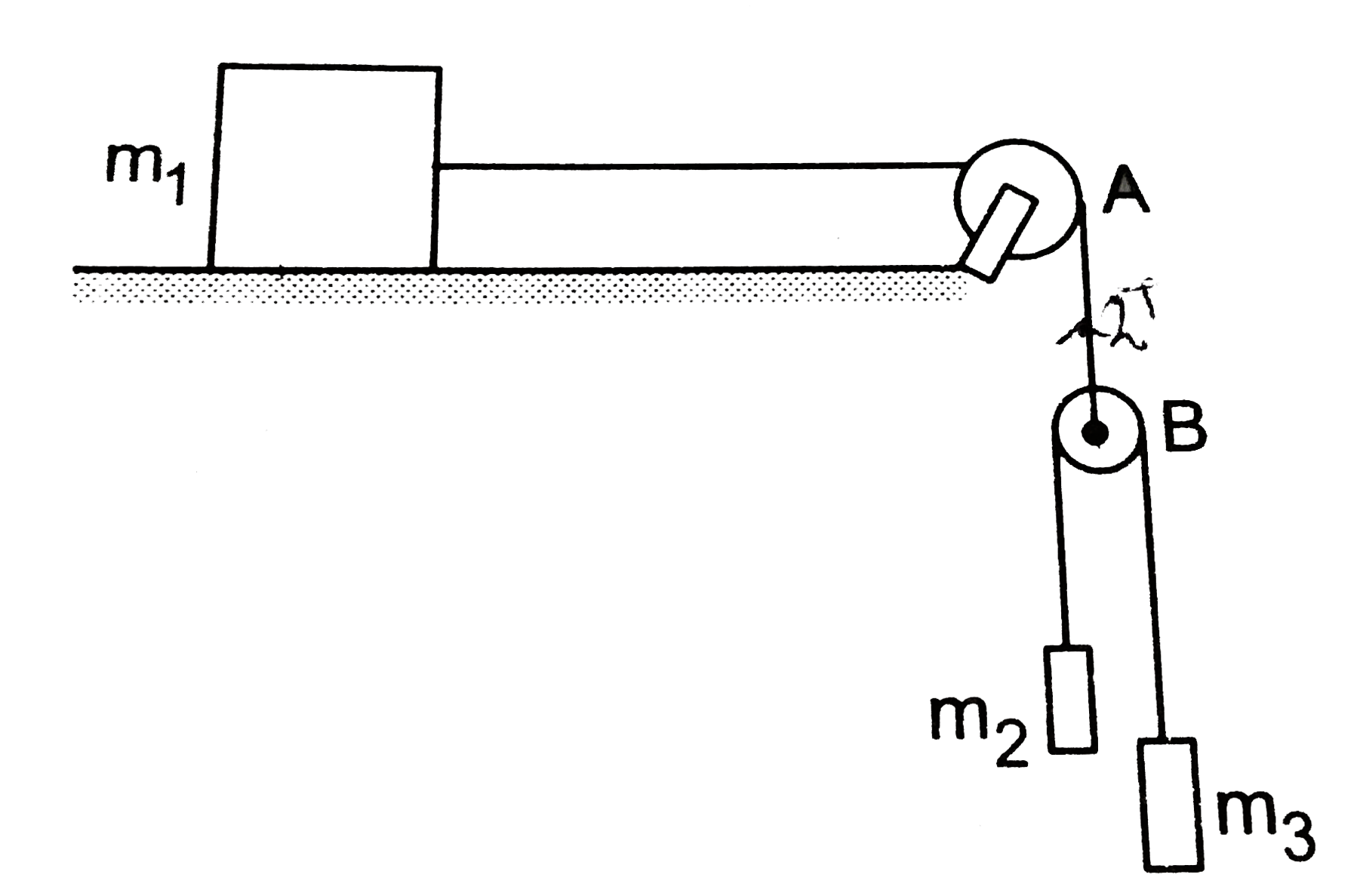
View SolutionWhen we ignore friction and mass of pulley what would be the accelerations of the two blocks m1 and m2
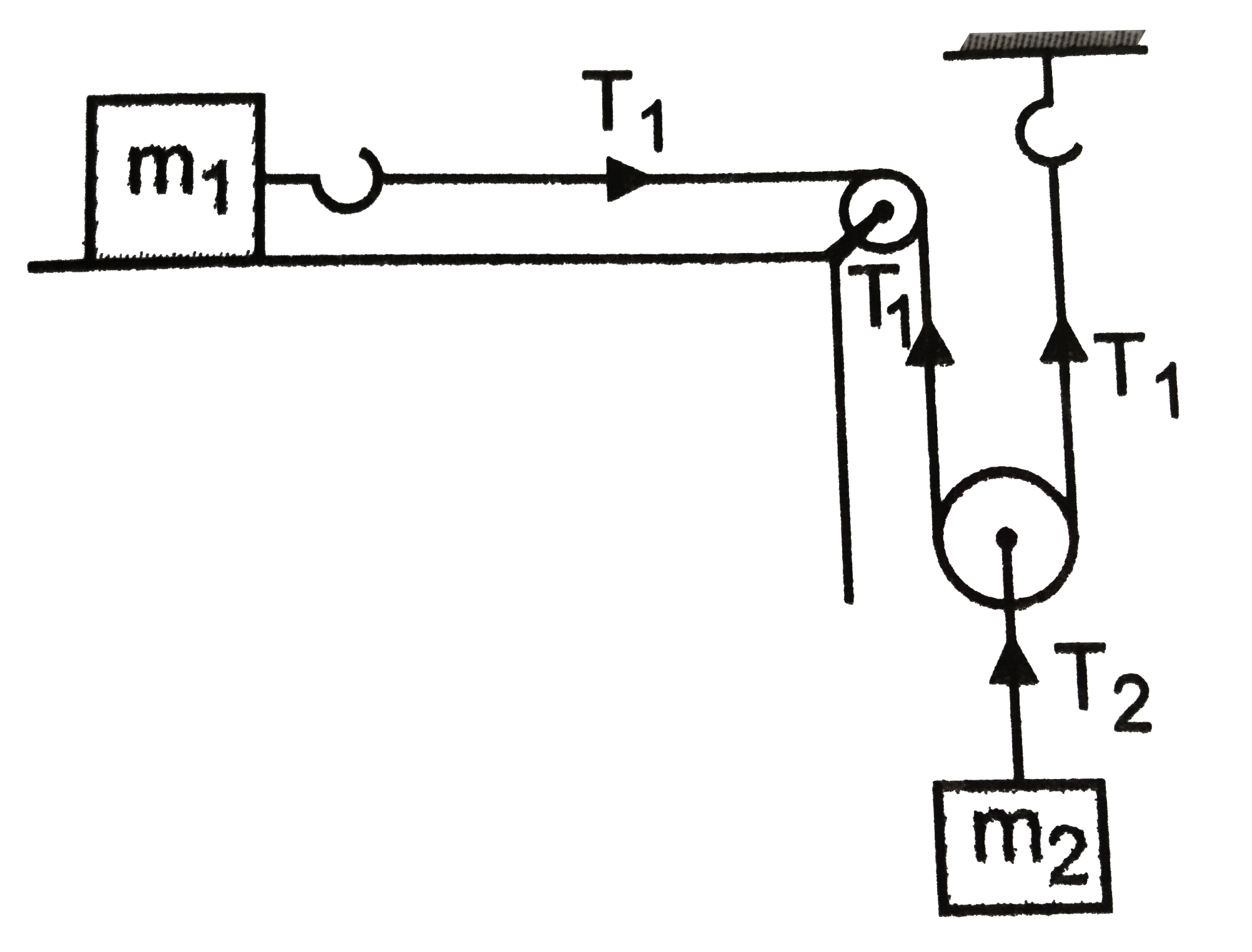 .
.
View SolutionTwo masses m1 and m2 are connected by light inextensible string passing over a smooth pulley P. If the pulley moves vertically upwards with an acceleration equal to g then
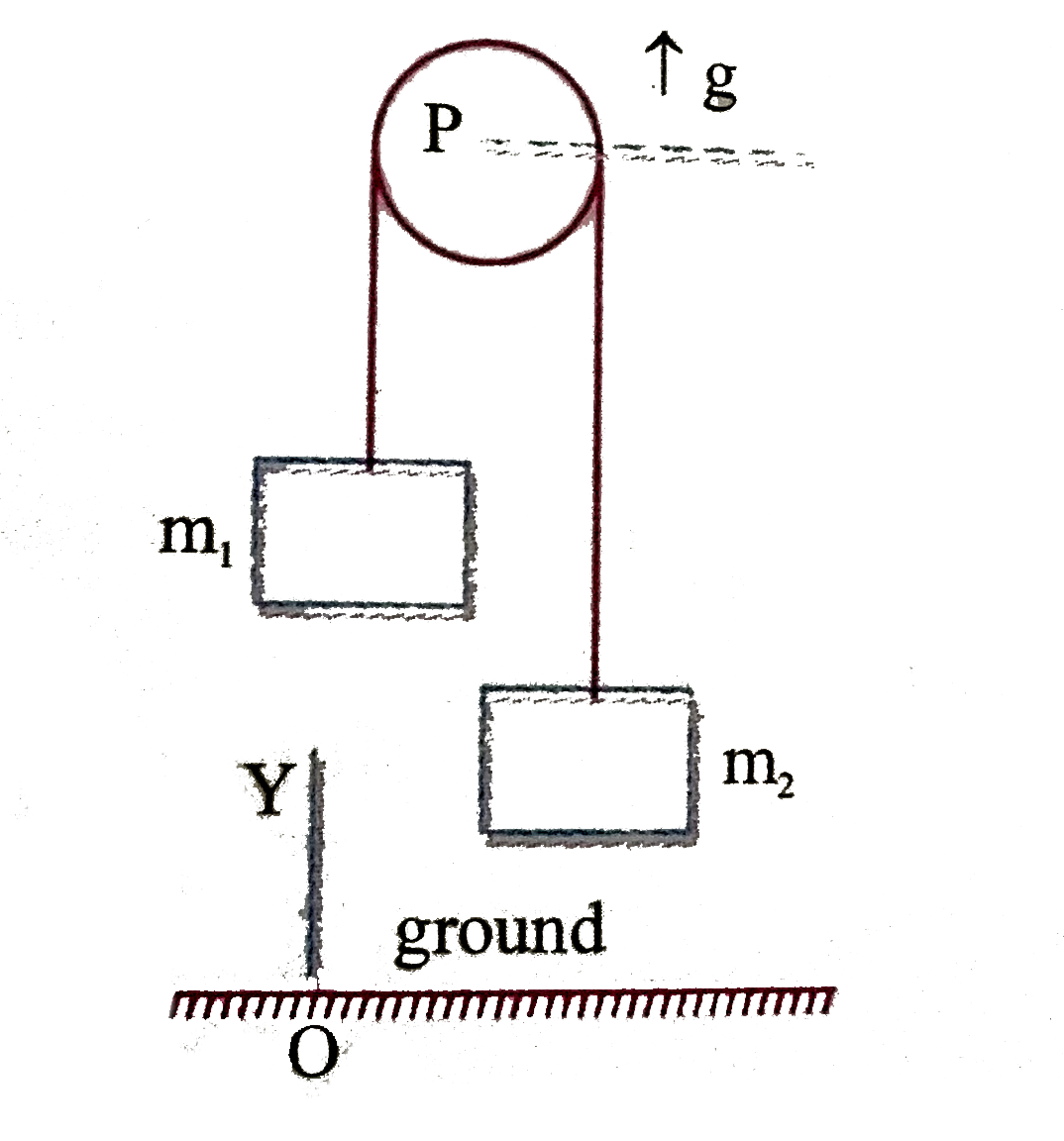 .
.
View SolutionThree block of masses m1,m2 and m3 kg are placed in contact with each other on a frictionless table. A force F is applied on the heaviest mass m1, the acceleration of m2 will be

View SolutionTwo blocks of masses m1 and m2 are connected by a string of negligible mass which pass over a frictionless pulley fixed on the top of an inclined plane as shown in figure. The coefficient of friction between m1 and plane is μ.
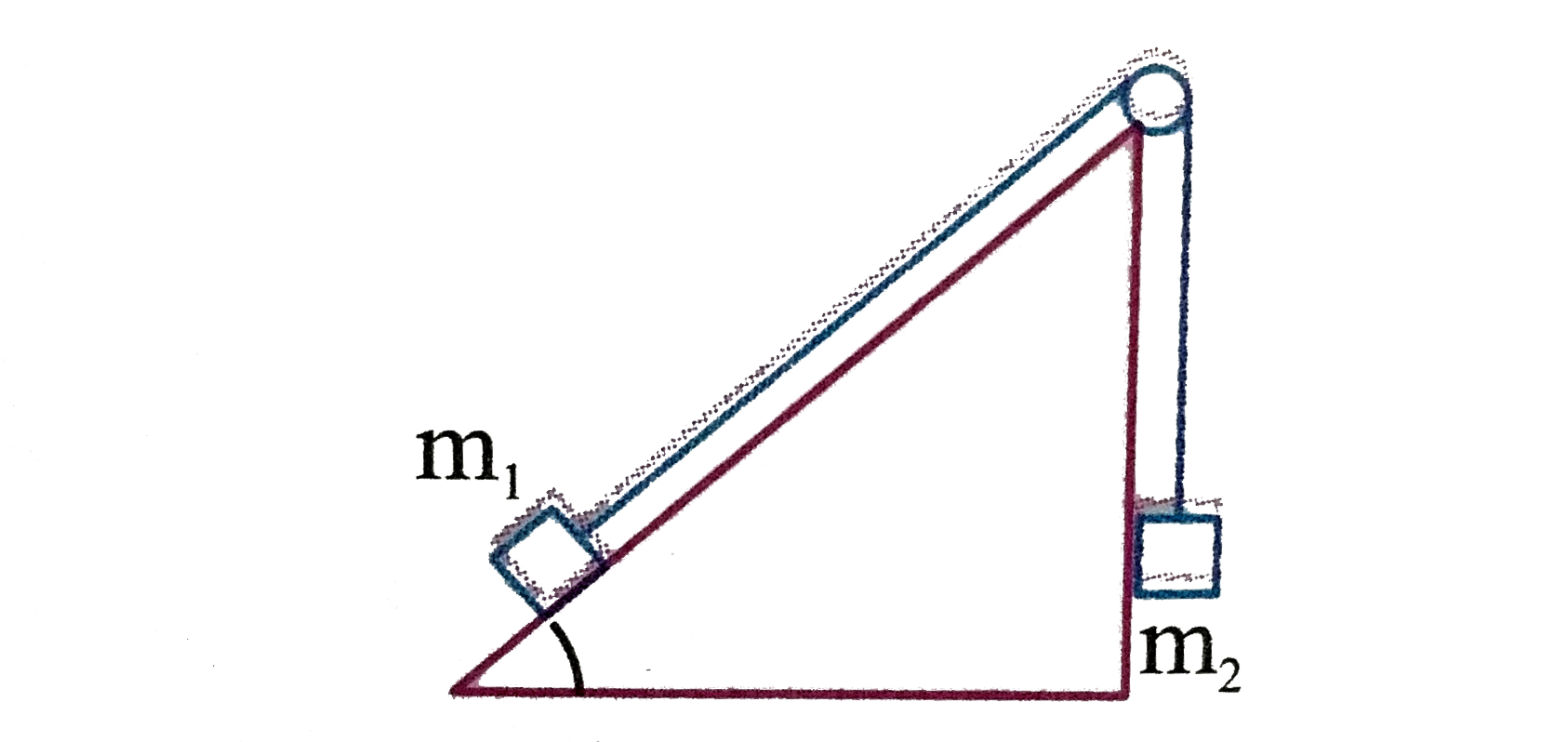
View Solution
