A table with smooth horizontal surface is fixed in a cabin that rotates with a uniform angular velocity ω in a circular pathof radius R. A smooth groove AB of length L(<<R) is made on the surface of the table. The groove makes an angleθ with the radius OA of the circle in which the cabin rotates. A small particle is kept at the point A in the groove and is released to move along AB. Find the time taken by tehparticle to reach the point B.
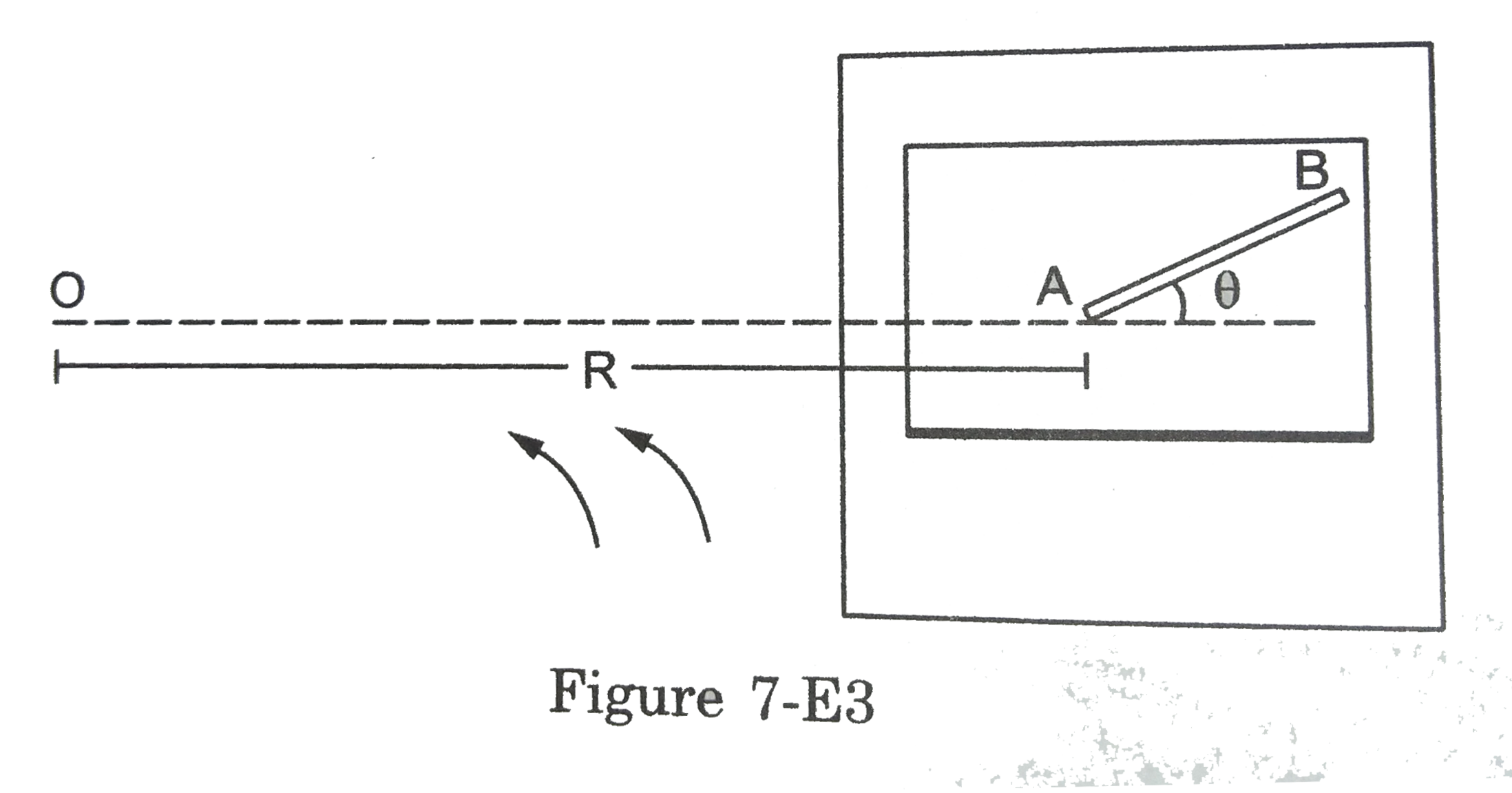
Since the table rotates with the uniform angular velocity w. hence particle also rotates with the same angular velocity .
Since, centrifugal force acting on the particle is in a directiion paraller to OA , hence in component along the length of the grove=mω2rcosθ
If a be the acceleration of the particle along the groove, then
a=ω2rcosθ
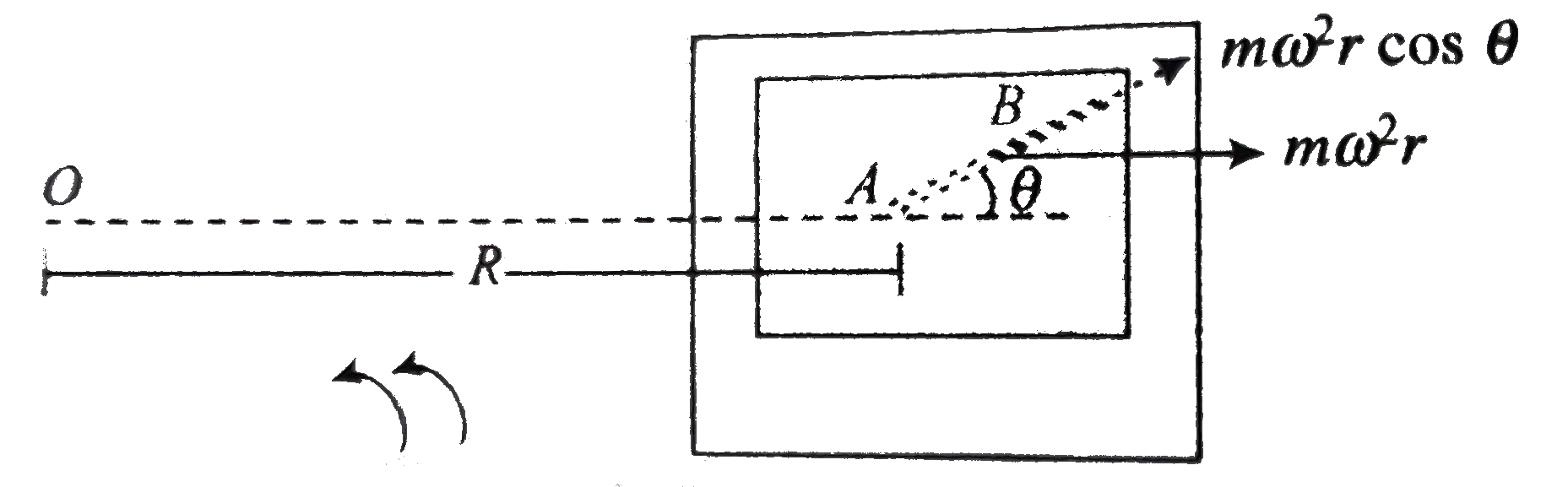
As the length of groove ABL(<<R) ,we can take the radius of rotation of the particle while moving on constant and equal to r=R
Hence the acceleration a of the particle along the groove will be constant then
a=ω2Rcosθ
Hence the time required by the particle to reach the end B of the groove, using
L=ut+12at2, Here u=0,a=ω2Rcosθ
rArt=√2Lω2Rcosθ
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Subjective
21 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Single Correct
87 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Exercise 7.2
16 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Integer
5 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE
2 Videos
Similar Questions
A table with smooth horizontal surface is turning at an angular speed ω about its axis. A groove is made on the surface along a radius and a particle is gently placed inside the groove at a distance a from the centre. Find the speed of the speed of the particle as its distance from the centre becomes L.
View SolutionA table with smooth horizontal surface is turning at an angular speed ω about its axis. A groove is made on the surface along a radius and a particle is gently placed inside the groove at a distance a from the centre. Find the speed of the speed of the particle as its distance from teh centre becomes L.
View SolutionA table with smooth horiztonal surface is truning at an angular speed ω abouyt its axis. A groove is made on the surface along a radius and a particle is gently placed inside the groove at a distance a from the centre. Find the speed of the speed of the particle as its distance from teh centre becomes L.
View SolutionA ring of radius 'r' and mass per unit length 'm' rotates with an angular velocity 'ω' in free space then tension will be :
View SolutionA particle is revolving in a circle of radius r and centre at 'O' with uniform angular velocity ω. Choose the correct option(s) :

View SolutionTyres are grooved to
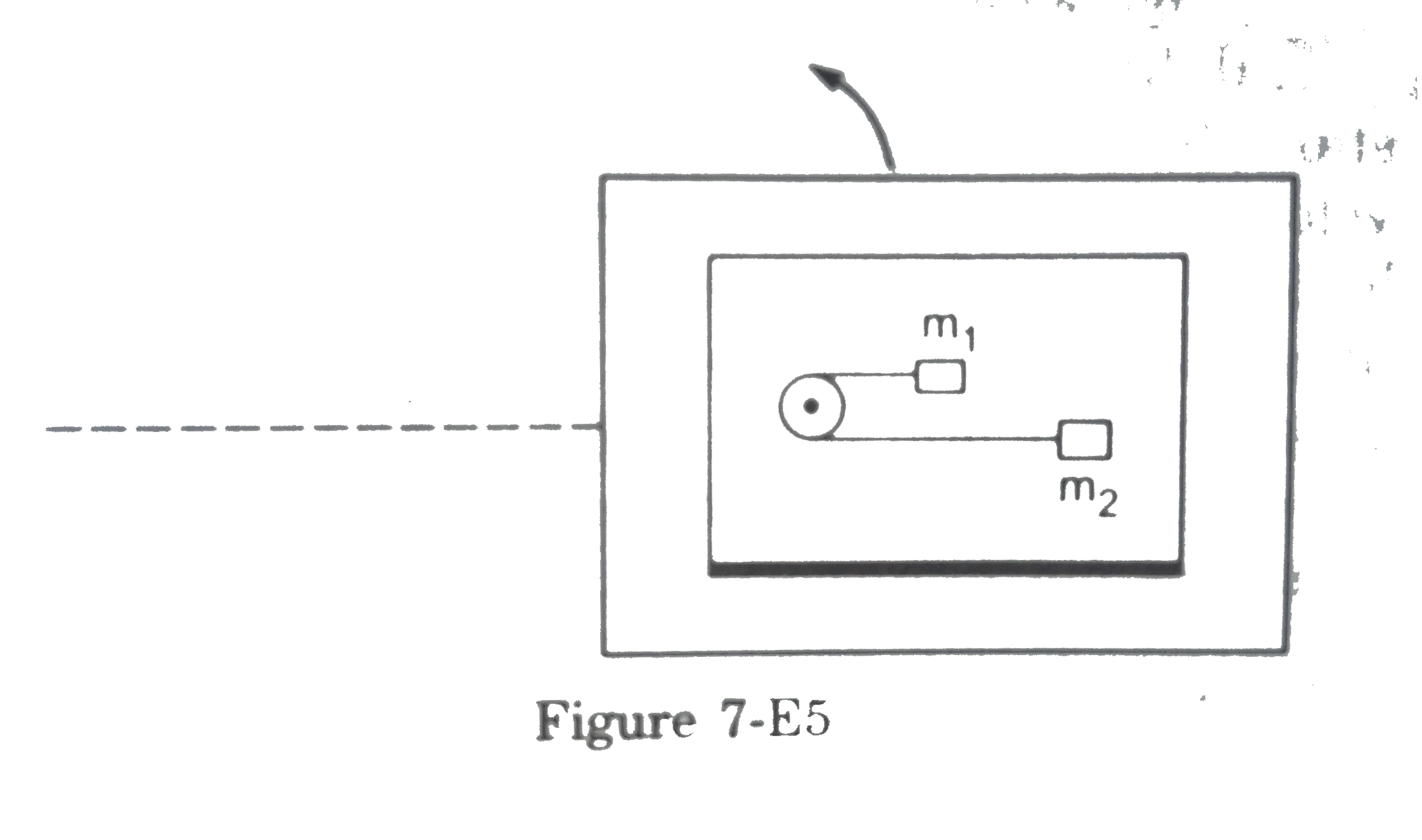
View SolutionA table with smooth horizontal surface is placed in a cabin which moves in a circle of a large radius R Figure. A smooth pulley of small radius is fastened to the table. Two masses m and 2m placed on te tableare connected through a string going over the pulley. Initially the masses are held by a personwith the strings aslong teh outward radius and then the system is released from rest (with respect to the cabin). Find the magnitude of the initial acceleration of the mases as seen from the cabin and the tension in the starting.
View SolutionA rod of length l rotates with a small but uniform angular velocity ω about its perpendicular bisector. A uniform magnetic field B exists parallel to the axis of rotation. The potential difference between the centre of the rod and an end is
View SolutionA uniform stick of length l and mass m lies on a smooth table. It rotates with angular velocity ω about an axis perpendicular to the table and through one end of the stick. The angular momentum of the stick about the end is
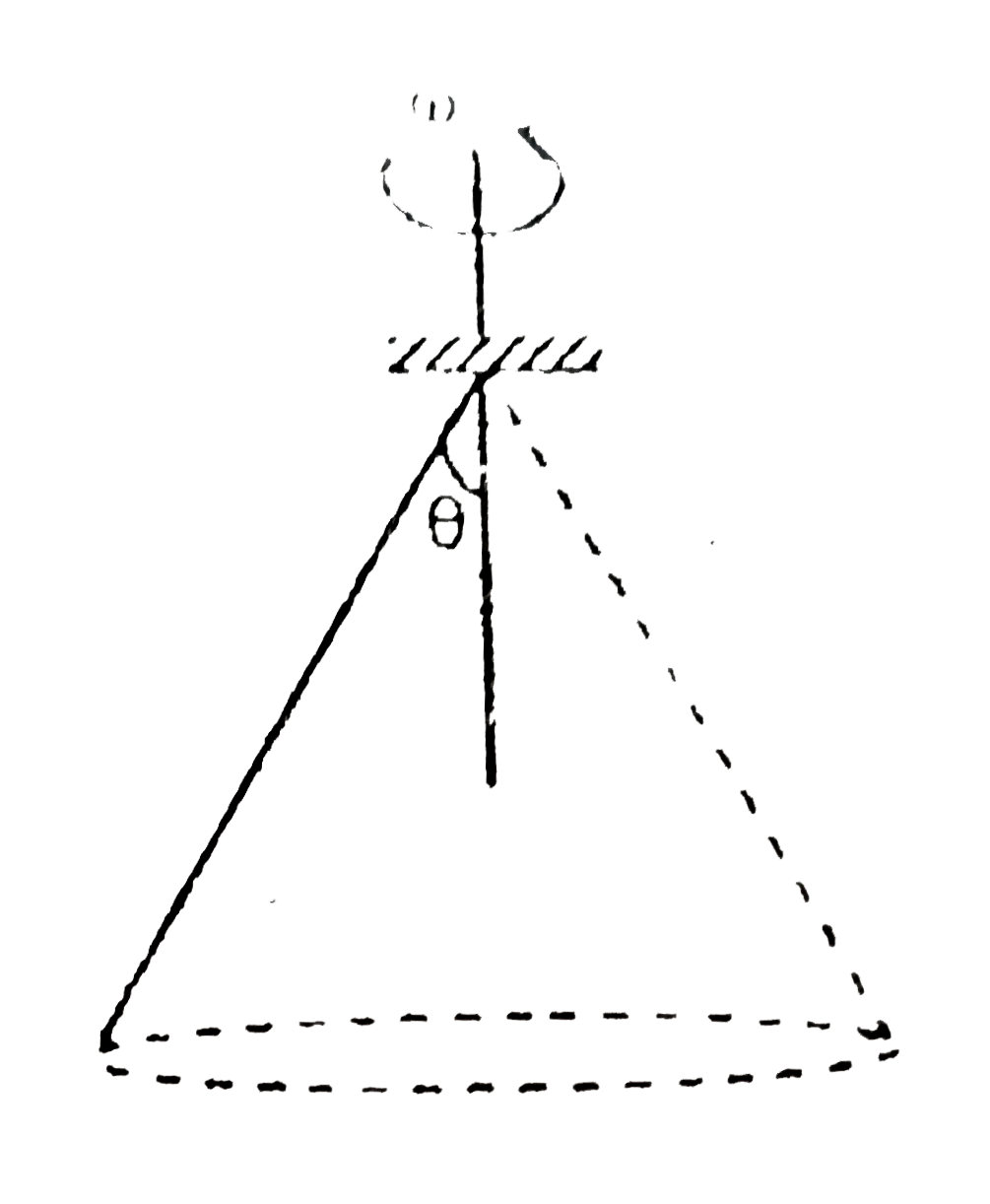
View SolutionA rod of mass m and length l is rotating about a fixed point in the ceiling with an angular velocity ω as shown in the figure. The rod maintains a constant angle θ with the vertical.
What angle will the rod make with the vertical
View Solution
