A ring of radius 'r' and mass per unit length 'm' rotates with an angular velocity 'ω' in free space then tension will be :
zero
12mω2r2
mω2r2
mrω2
The correct Answer is:C
To solve the problem of finding the tension in a rotating ring, we can follow these steps:
1. Understanding the System:
- We have a ring of radius r and mass per unit length m rotating with an angular velocity ω.
- The ring is in free space, meaning there are no external forces acting on it.
2. Identifying Forces:
- Consider a small segment of the ring subtending an angle dθ at the center. The length of this segment is rdθ.
- The mass of this small segment is given by mass=mass per unit length×length=m⋅(rdθ).
3. Centripetal Force Requirement:
- For the segment to maintain circular motion, a net centripetal force must act towards the center of the ring. This force can be provided by the tension in the ring.
- The tension T in the ring creates components that contribute to the centripetal force.
4. Components of Tension:
- The tension T acts along the ring, and we can resolve it into components. Each side of the segment contributes a component of tension towards the center.
- The vertical component of tension towards the center is Tsin(dθ2) from each side, giving a total contribution of 2Tsin(dθ2).
5. Setting Up the Equation:
- The net centripetal force required for the mass m⋅(rdθ) moving with velocity v is given by:
Fcentripetal=m⋅(rdθ)⋅v2r
- Since v=ωr, we can substitute to get:
Fcentripetal=m⋅(rdθ)⋅(ωr)2r=m⋅(rdθ)⋅ω2r
6. Equating Forces:
- Set the centripetal force equal to the net tension force:
2Tsin(dθ2)=m⋅(rdθ)⋅ω2r
7. Simplifying the Equation:
- For small angles, sin(dθ2)≈dθ2. Thus, we can rewrite the equation as:
2T⋅dθ2=m⋅(rdθ)⋅ω2r
- This simplifies to:
Tdθ=m⋅r2⋅ω2dθ
8. Final Result:
- Canceling dθ from both sides (assuming dθ≠0):
T=m⋅r2⋅ω2
Conclusion:
The tension T in the ring is given by:
T=m⋅r2⋅ω2
- We have a ring of radius r and mass per unit length m rotating with an angular velocity ω.
- The ring is in free space, meaning there are no external forces acting on it.
- Consider a small segment of the ring subtending an angle dθ at the center. The length of this segment is rdθ.
- The mass of this small segment is given by mass=mass per unit length×length=m⋅(rdθ).
- For the segment to maintain circular motion, a net centripetal force must act towards the center of the ring. This force can be provided by the tension in the ring.
- The tension T in the ring creates components that contribute to the centripetal force.
- The tension T acts along the ring, and we can resolve it into components. Each side of the segment contributes a component of tension towards the center.
- The vertical component of tension towards the center is Tsin(dθ2) from each side, giving a total contribution of 2Tsin(dθ2).
- The net centripetal force required for the mass m⋅(rdθ) moving with velocity v is given by:
Fcentripetal=m⋅(rdθ)⋅v2r
- Since v=ωr, we can substitute to get:
Fcentripetal=m⋅(rdθ)⋅(ωr)2r=m⋅(rdθ)⋅ω2r
- Set the centripetal force equal to the net tension force:
2Tsin(dθ2)=m⋅(rdθ)⋅ω2r
- For small angles, sin(dθ2)≈dθ2. Thus, we can rewrite the equation as:
2T⋅dθ2=m⋅(rdθ)⋅ω2r
- This simplifies to:
Tdθ=m⋅r2⋅ω2dθ
- Canceling dθ from both sides (assuming dθ≠0):
T=m⋅r2⋅ω2
The tension T in the ring is given by:
T=m⋅r2⋅ω2
Topper's Solved these Questions
- CIRCULAR MOTIONBOOK - ALLENCHAPTER - CIRCULAR MOTIONEXERCISE - EXERCISE (J-M)
5 Videos
- CIRCULAR MOTIONBOOK - ALLENCHAPTER - CIRCULAR MOTIONEXERCISE - EXERCISE (J-A)
6 Videos
- CIRCULAR MOTIONBOOK - ALLENCHAPTER - CIRCULAR MOTIONEXERCISE - Martrix match
1 Videos
- BASIC MATHSBOOK - ALLENCHAPTER - BASIC MATHSEXERCISE - Question
1 Videos
- CURRENT ELECTRICITYBOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - EX.II
66 Videos
Similar Questions
A ring of mass m and radius R is being rotated about its axis with angular velocity o. If o increases then tension in ring
View SolutionA rod has length 'l' and mass per unit length linearly increases from λ to 2λ as shown in figure. Rod rotates with constant angular velocity ω in a gravity free space. Find the tension (in Newton) in the rod at its middle point. (take ωl=2m/secandλ=3kg/m)

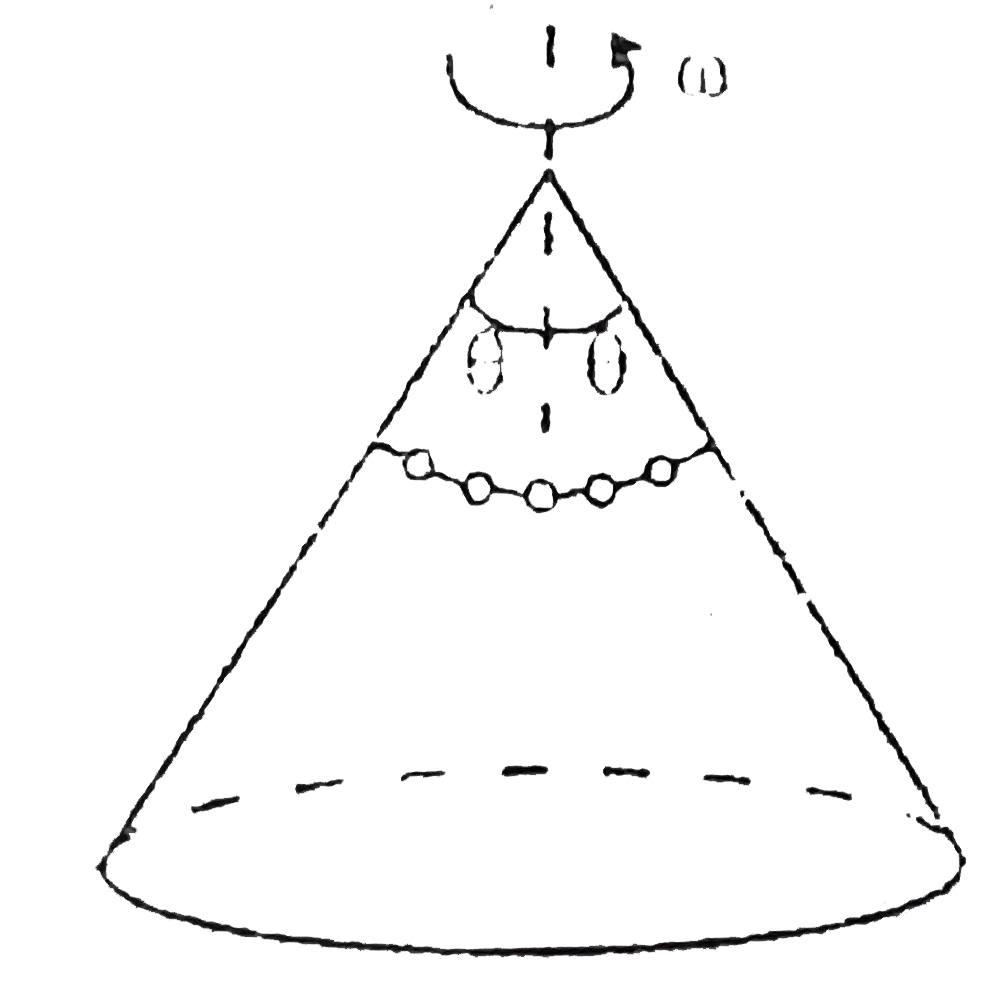
View SolutionA chain of mass 'm' and radius 'r' is placed onto a cone of semi vertical angle θ. Cone rotated with angular velocity ω. Find the tension in the chain if it does not slide on the cone.
View SolutionA ring of radius R is first rotated with an angular velocity ω and then carefully placed on a rough horizontal surface. The coefficient of friction between the surface and the ring is μ. Time after which its angular speed is reduced to half is
View SolutionA string has a linear mass density μ. The ends of the string are joined to form a closed loop and is given the shape of a circular ring of radius R. this ring is now rotated about its axis with an angular velocity ω
Q. The tension developed in the string is
View SolutionA thin disc of radius R has charge Q distributed uniformly on its surface. The disc is rotated about one of its diametric axis with angular velocity ω. The magnetic moment of the arrangement is
View SolutionA string has a linear mass density μ. The ends of the string are joined to form a closed loop and is given the shape of a circular ring of radius R. this ring is now rotated about its axis with an angular velocity ω
Q. The velocity of the transverse wave set up in the string, with respect to an observer at the centre of
View SolutionA thin uniform ring of radius R carrying charge q and mass m rotates about its axis with angular velocity ω. Find the ratio of its magnetic moment and angular momentum.
View SolutionA non-conducting ring of radius R has charge Q distributed unevenly over it. If it rotates with an angular velocity ω the equivalent current will be:

View SolutionThere is a ring of radius r having linear charge density λ and rotating with a uniform angular velocity ω. the magnetic field produced by this ring at its own centre would be
View Solution
