A tangential force F acts at the top of a disc of a mass m and radius R . If it rolls without slipping. Then
Let f be the force of friction between the shell and the horizontal surface
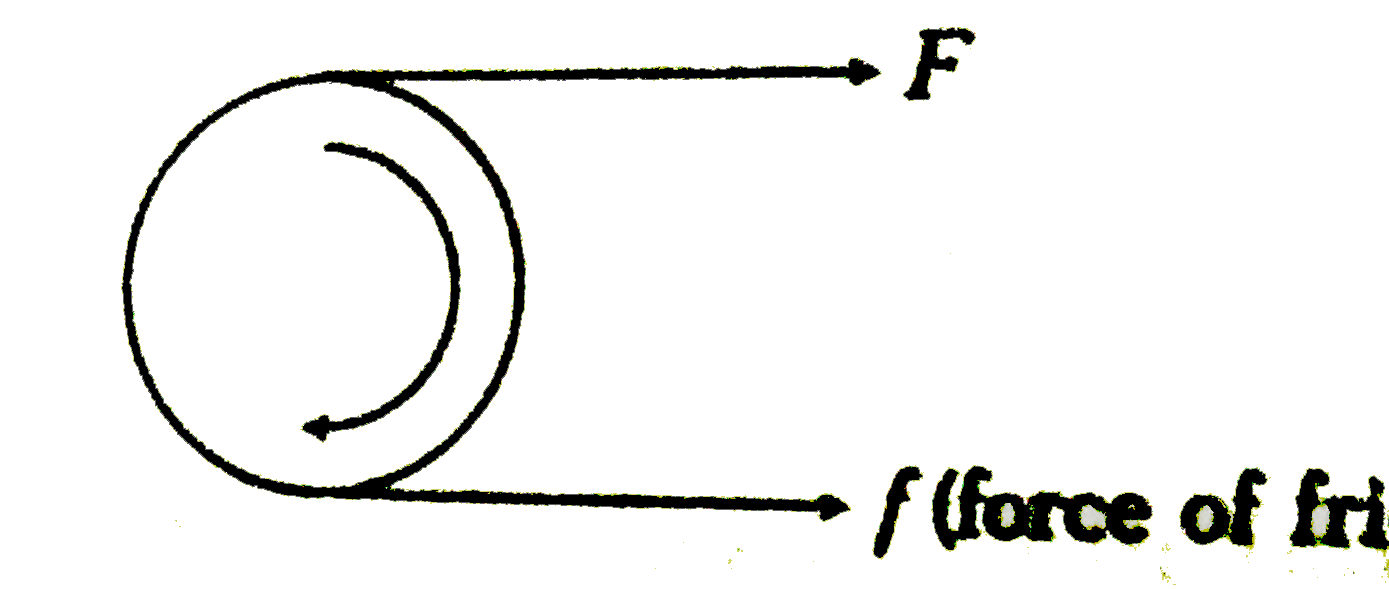
For translational motion
F+f=ma ….(i)
For rotational motion,
FR−fR=Iα=IaR(∵a=Rαfor pure rolling)
⇒F−f=IaR2...(ii)
Adding Eqs. (i) and (ii)
2F=(m+IR2)a=(m+23m)a=53ma
or F=56ma [∵Ishell=23mR2]
⇒a=6F5m.
Topper's Solved these Questions
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - Check point 9.1
20 Videos
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - Check point 9.2
20 Videos
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Integer type q.
14 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
Similar Questions

A tangential force F acts at the top of a thin spherical shell of mass m and radius R. Find the acceleration of the shell if it rolls without slipping.
View SolutionA particle of mass 'm' is attached to the rim of a uniform disc of mass 'm' and radius R. The disc is rolling wihtout slipping on a stationery horizontal surface as shown in the figure. At a particular instant, the particle is at the topmost position and centre of the disc has speed v0 amd its angular speed is ω. Choose the correct option (s).
View Solution
Knowledge Check

A tangential force F acts at the top of a thin spherical shell of mass m and radius R. Find the acceleration of the shell if it rolls without slipping.Aa. Acceleration of disc = 2F/3mBb. Friction force between disc and surface = 2F/3Cc. Acceleration of disc = 6F/5mDd. Friction force between disc and surface is F/3
Work energy theorem sys work done by all the force is equal to change in kinetic energy" In the diagram, a disc of mass M and radius Ris rolling without slipping on a rough fixed inclined AB=l,V= velocity of disc at B.
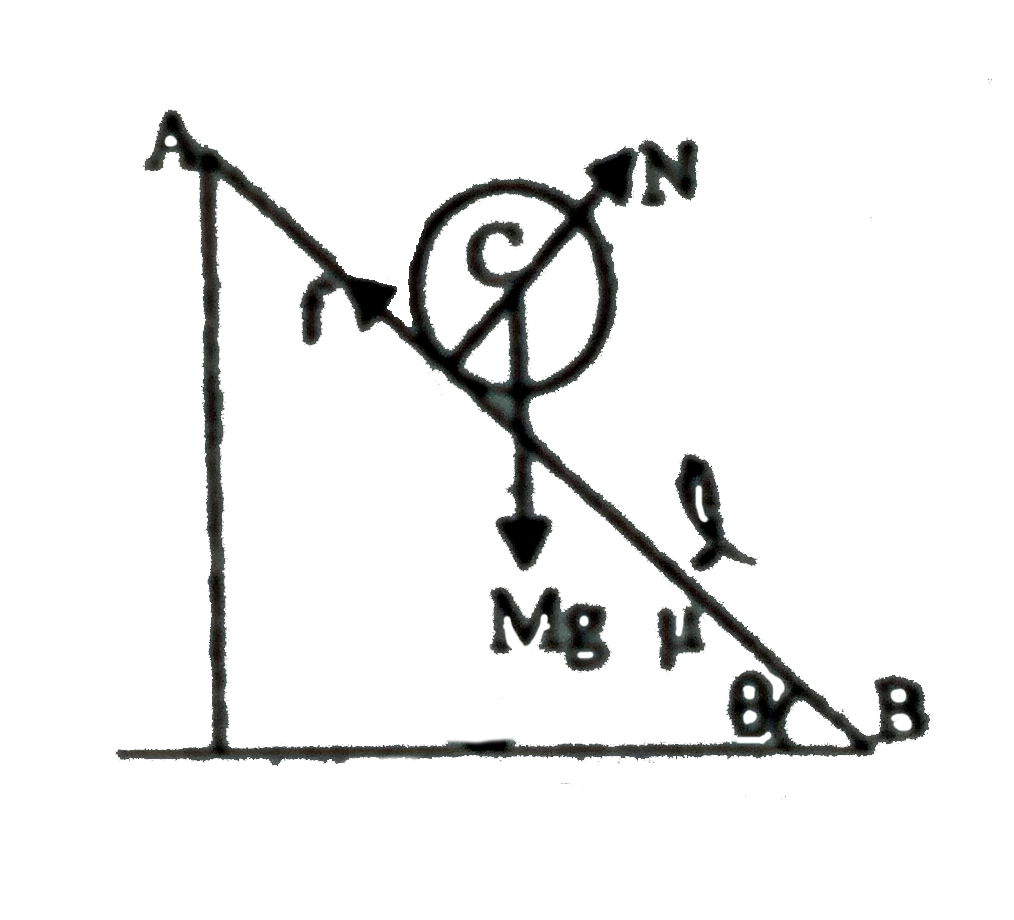
Choose the correct option(s)
View SolutionWork energy theorem sys"work done by all the force is equal to change in kinetic energy" In the diagram, a disc of mass M and radius Ris rolling without slipping on a rough fixed inclined AB=l,V= velocity of disc at B.
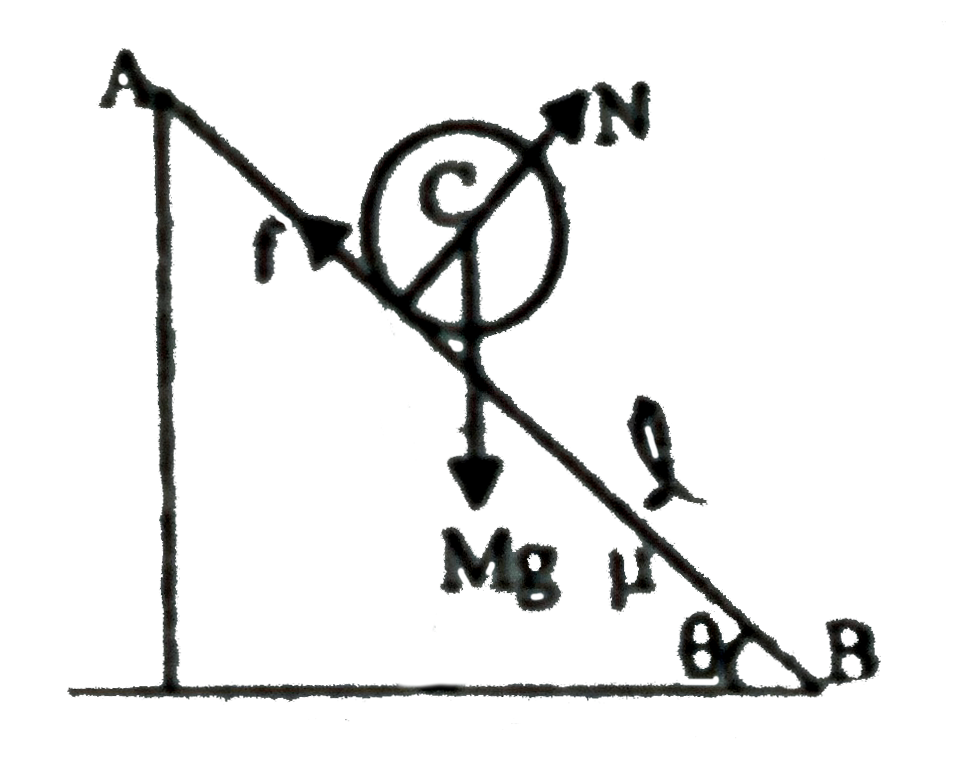
Choose the correct option(s)
View SolutionA horizontal force F=14N acts at the centre of mass of a sphere of mass m=1kg. If the sphere rolls without sliding, find the frictional force (in N)

View Solution
In the figure shown, a force F is applied at the top of a disc of mass 4 kg and radius 0.25 m. find maximum velue of F for no slipping.
View SolutionIf a tangential force mg is applied to a disc of mass m and radius r, the angular acceleration produced in it is?
View SolutionThree forces of magnitude F, F and √2F are acting on the periphery of a disc of mass m and radius R as shown in the figure. The net torque about the centre of the disc is
View SolutionA force F acts tangentially at the highest point of a disc of mass m kept on a rough horizontal plane. If the disc rolls without slipping, the acceleration of centre of the disc is:

View Solution
