Three forces of magnitude F, F and √2F are acting on the periphery of a disc of mass m and radius R as shown in the figure. The net torque about the centre of the disc is
FRˆK
−FRˆK
3FRˆK
−3FRˆK
The correct Answer is:B
To solve the problem of calculating the net torque about the center of the disc due to the three forces acting on it, we can follow these steps:
1. Identify the Forces and Their Directions:
- We have three forces: F, F′ (which we can denote as F for simplicity), and √2F.
- The force √2F is acting at an angle of 45∘ with respect to the radius of the disc.
2. Calculate the Torque Due to Each Force:
- Torque (τ) is calculated using the formula:
τ=r×F×sin(θ)
- Where r is the radius of the disc, F is the force applied, and θ is the angle between the force and the radius.
3. Torque from the Force F:
- The torque due to the force F acting tangentially (assuming it acts perpendicular to the radius):
τ1=R⋅F⋅sin(90∘)=R⋅F
4. Torque from the Force F′:
- The torque due to the second force F′ (acting in the opposite direction):
τ2=R⋅F′⋅sin(90∘)=R⋅F
- This torque will act in the opposite direction, so we consider it as negative.
5. Torque from the Force √2F:
- The torque due to the force √2F acting at an angle of 45∘:
τ3=R⋅√2F⋅sin(45∘)=R⋅√2F⋅√22=R⋅F
- This torque will also act in the clockwise direction.
6. Calculate the Net Torque:
- Now, we can sum up the torques considering their directions:
Net Torque=τ1−τ2+τ3=R⋅F−R⋅F+R⋅F=R⋅F
- Since τ2 is negative, it cancels out τ1, leaving us with the torque from √2F.
7. Final Result:
- The net torque about the center of the disc is:
τnet=−R⋅F^k
- The negative sign indicates the direction of the torque.
- We have three forces: F, F′ (which we can denote as F for simplicity), and √2F.
- The force √2F is acting at an angle of 45∘ with respect to the radius of the disc.
- Torque (τ) is calculated using the formula:
τ=r×F×sin(θ)
- Where r is the radius of the disc, F is the force applied, and θ is the angle between the force and the radius.
- The torque due to the force F acting tangentially (assuming it acts perpendicular to the radius):
τ1=R⋅F⋅sin(90∘)=R⋅F
- The torque due to the second force F′ (acting in the opposite direction):
τ2=R⋅F′⋅sin(90∘)=R⋅F
- This torque will act in the opposite direction, so we consider it as negative.
- The torque due to the force √2F acting at an angle of 45∘:
τ3=R⋅√2F⋅sin(45∘)=R⋅√2F⋅√22=R⋅F
- This torque will also act in the clockwise direction.
- Now, we can sum up the torques considering their directions:
Net Torque=τ1−τ2+τ3=R⋅F−R⋅F+R⋅F=R⋅F
- Since τ2 is negative, it cancels out τ1, leaving us with the torque from √2F.
- The net torque about the center of the disc is:
τnet=−R⋅F^k
- The negative sign indicates the direction of the torque.
Similar Questions
A force of magnitude F is acting on rolling body of mass m and radius R as show in figure. What happens when it enters on a smooth surface?

View SolutionForces of equal magnitude of 0.5 N are acting on a square plate of side √2 m and mass 1 kg as shown in figure. The net torque on the square plate about centre O will be

View SolutionTwo forces of magnitude F are acting on a uniform disc kept on a horizontal rough surface as shown in the figure. Friction force by the horizontal surface on the disc is nF. Find the value of n.

View SolutionA force of magnitude F is acting on a rolling body of mass m and radius R as shown in figure. What happens if the pulling force F is removed ? Discuss the different posibilities when the pulling acts on the body.

a. At centre, b. Above centre, c. Below centre
View SolutionA disc of mass m and radius R is rolling without slipping as shown in the figure. The magnitude of net velocity of the point P is (OP=R2)
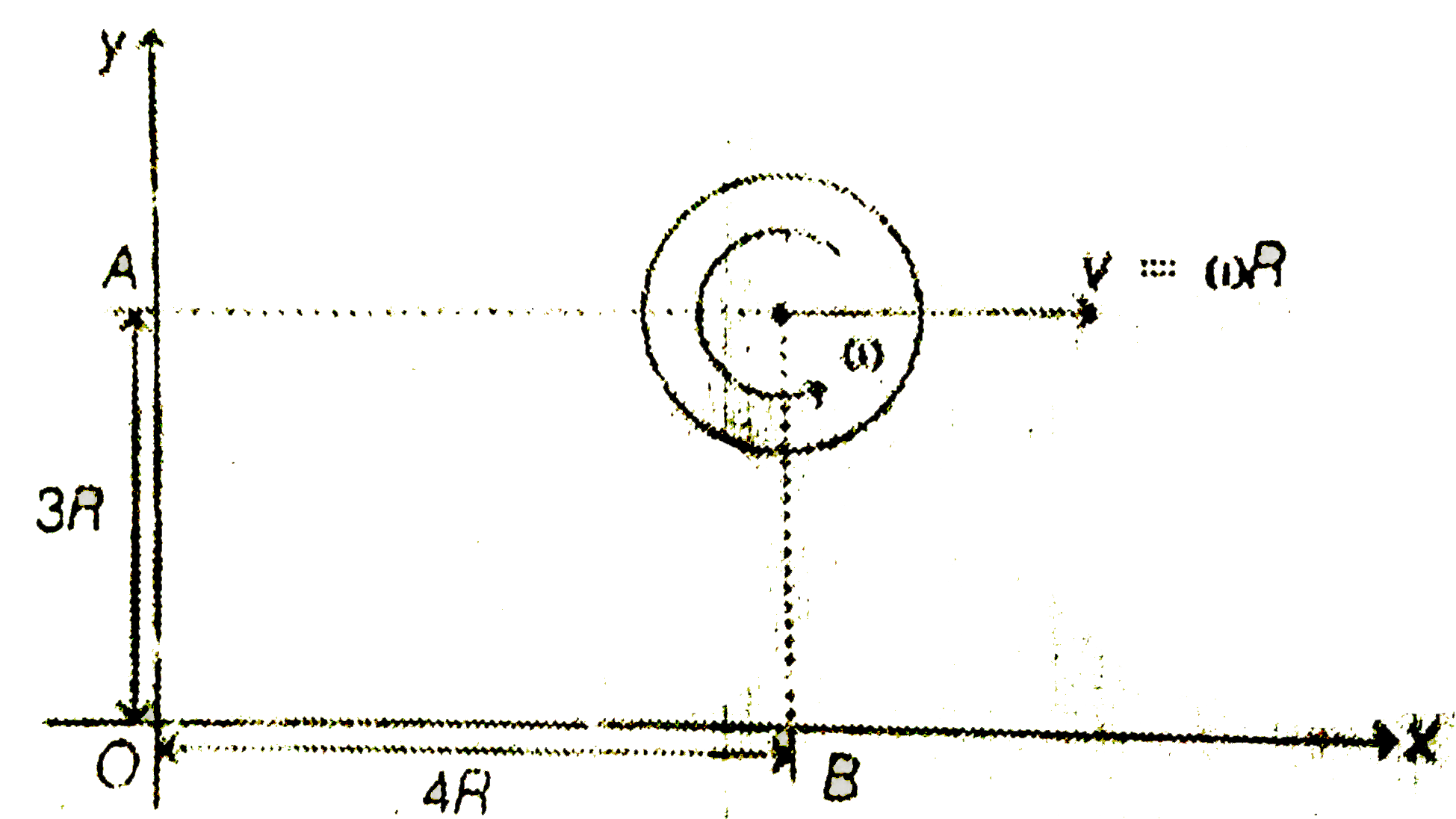
View SolutionA disc of mass M and radius R moves in the x-y plane as shown in the figure. The angular momentum of the disc at tihe instant shows is
View SolutionA system of uniform rod of mass m and length 2R and a uniform disc of m and radius R are as shown in the figure. The moment of inertia of the system about the axis OO′ (perpendicular to plane of disc) will be
View SolutionFrom a uniform disc of radius R, an equilateral triangle of side √3R is cut as shown in the figure. The new position of centre of mass is :

View SolutionA bullet of mass m collides inelastically at the periphery of a disc of mass M and radius R, with a speed v as shown. The disc rotates about a fixed horizontal axis. Find the angular velocity of the disc bullet system just after the impact.

View SolutionA force F acts tangentially on a part of a uniform disc of mass 'm' and radius 'R' hinged at point O. The force exerted by hinge on the portion of disc initially.

View Solution