A : The direction of a light is always perpendicular to wavefront
R : A ray of light is a line perpendicular to a wavefront in the direction of propagation.
Both A and R are true and R is the correct explanation of A
Both A and R are true and R is not the correct explanation of A
A is true and R is false
Both A and R are false
The correct Answer is:A
To analyze the statements given in the question, we need to evaluate each statement individually and determine their validity.
Step 1: Understanding the First Statement (A)
The first statement is: "The direction of a light is always perpendicular to wavefront."
- Explanation: A wavefront is defined as the locus of points that are in the same phase of a wave. For light waves, the direction of propagation of the wave is perpendicular to the wavefront. This means that if we consider a wavefront as a flat surface, the light rays (which represent the direction of light) will always make a right angle with this surface.
- Conclusion: The statement A is True.
Step 2: Understanding the Second Statement (R)
The second statement is: "A ray of light is a line perpendicular to a wavefront in the direction of propagation."
- Explanation: A ray of light is indeed represented as a straight line that indicates the path along which light energy travels. By definition, this ray is perpendicular to the wavefront, which means that it points in the direction of the wave's propagation.
- Conclusion: The statement R is also True.
Step 3: Evaluating the Relationship between A and R
Now that we have established that both statements A and R are true, we need to determine if R is a correct explanation of A.
- Analysis: Since R accurately describes the relationship between the direction of light and the wavefront, we can conclude that R is indeed a correct explanation for A.
Final Conclusion
Both statements A and R are true, and R is a correct explanation of A.
Summary
- Statement A: True
- Statement R: True
- R is a correct explanation of A.
The first statement is: "The direction of a light is always perpendicular to wavefront."
The second statement is: "A ray of light is a line perpendicular to a wavefront in the direction of propagation."
Now that we have established that both statements A and R are true, we need to determine if R is a correct explanation of A.
Both statements A and R are true, and R is a correct explanation of A.
- Statement A: True
- Statement R: True
- R is a correct explanation of A.
Topper's Solved these Questions
- WAVES OPTICSBOOK - AAKASH SERIESCHAPTER - WAVES OPTICSEXERCISE - EXERCISE -II (INTERFERENCE)
26 Videos
- WAVES OPTICSBOOK - AAKASH SERIESCHAPTER - WAVES OPTICSEXERCISE - EXERCISE -II (DIFFRACTION)
17 Videos
- WAVES OPTICSBOOK - AAKASH SERIESCHAPTER - WAVES OPTICSEXERCISE - EXERCISE -IA (ASCENDING AND DSCENDING ORDER TYPE QUESTIONS)
6 Videos
- WAVESBOOK - AAKASH SERIESCHAPTER - WAVESEXERCISE - EXERCISE-III (Doppler effect :)
15 Videos
Similar Questions
Direction of light is detected by
View SolutionAssertion In electromagnetic wave, if direction of veriations of electric and magnetic field are perpendicular to each other and also perpendicular to the direction of wave propagation.
Reason Electronegative waves are transverse in nature.
View Solution
Knowledge Check
Assertion : Electromagnetic waves are transverse in nature
Reason : The electric and magnetic fields in electromagnetic waves are perpendicular to each other and to the direction of propagation.AIf both assertion and reason are true and reason is the correct explanation of assertionBIf both assertion and reason are true but reason is not the correct explanation of assertionCIf assertion is true but reason is falseDIf both assertion and reason are false
Wavefront of a wave has direction with wave motion
View SolutionThe direction ratios of the perpendicular from the origin to a plane are 12,-3,4 and the length of the perpendicular is 5. Find the equation of the plane.
View SolutionThe ray of light after striking the mirror moves in same direction.
View SolutionHow is a wavefront related to the direction of corresponding rays ?
View SolutionHuygen was the first scientist who proposed the idea of wave theory of light. He said that the light propagates in form of wavefronts. A wavefront is an imaginary surface at every point of which waves are in the same phase. For example the wavefronts for a point source of light is collectionof concentric spheres which have centre at the origin. w1 is a wavefront. w2 is another wavefront.

The redius of the wavefront at time 't' is 'ct' in this case where 'c' is the speed of light. The direction of propagation of light is perpendicular to the surface of the wavefront. The wavefronts are plane wavefronts in case of a parallel beam of light.

Huygen also said that every point of the wavefront acts as the source of secondary wavelets. The tangent drawn to all secondary wavelets at a time is the new wavefront at that time. The wavelets are to be consid-ered only in the forward direction (i.e. the direction of propagation of light) and not in the reverse direction. If a wavefront w1 at time t is given, then to draw the wavefront at time t+Δt0 take some points on the wavefront w1 and draw spheres of radius 'cΔt'. They are called secondary wavelets
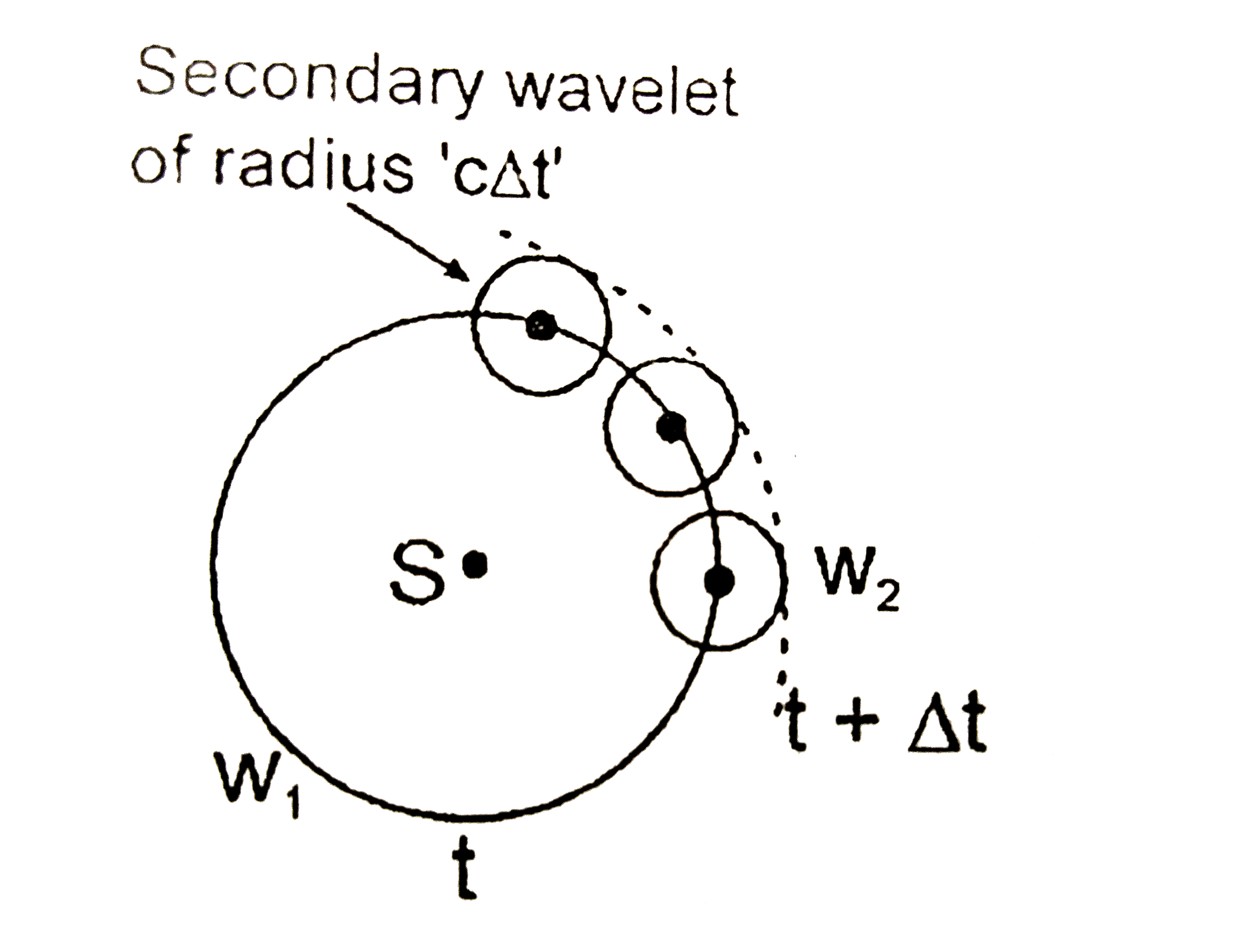
Draw a surface w2 which is tangential to all these secondary wavelets. w2 is the wavefront at time 't+Δt'. Huygen proved the laws of reflection and laws of refraction using concept of wavefronts.
A point source of light is placed at origin, in air. The equation of wave front of the wave at time t, emitted by source at t=0, is (take refractive index of air as 1)
View SolutionWill a vertical line and a horizontal line always be perpendicular to each other?
View SolutionFind the equation of a line which is at a perpendicular distance of √2 units from origin and the perpendicular from origin to this line makes an angle of 135∘ from positive direction of X-axis.
View Solution
