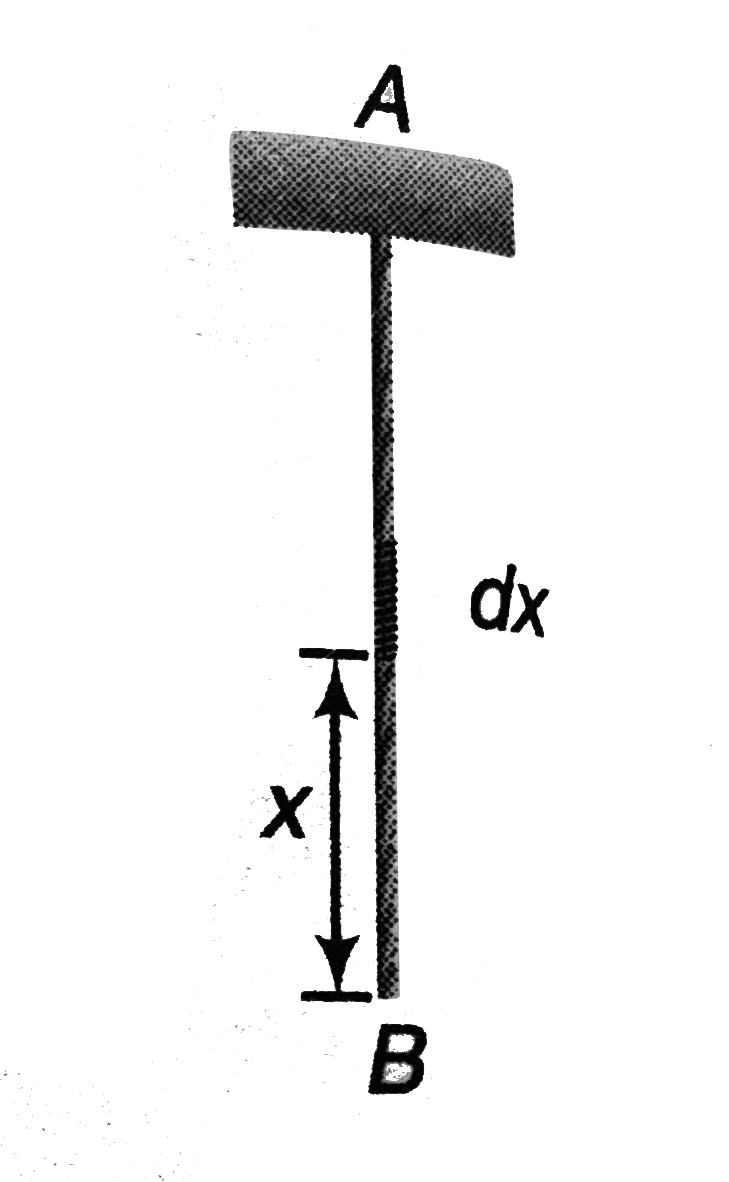
A thick rope of density ρ and length L is hung from a rigid support. The increase in length of the rope due to its own weight is (Y is the Young's modulus)
Let A be the area of corsssection of the rope. Weight of the rope, F=ALρg. It will be acting at the centre of gravity of the rope which lies at a distance L/2 form the rigid support. Therefore,
Y=normal stresslongitudinal stress=ALrohg/AΔL/(L/2)
or ΔL=L2ρg2Y.
Topper's Solved these Questions
- PROPERTIES OF BULK MATTERBOOK - PRADEEPCHAPTER - PROPERTIES OF BULK MATTEREXERCISE - Long Answer questions
33 Videos
- PROPERTIES OF BULK MATTERBOOK - PRADEEPCHAPTER - PROPERTIES OF BULK MATTEREXERCISE - Solved Examples
159 Videos
- PROPERTIES OF BULK MATTERBOOK - PRADEEPCHAPTER - PROPERTIES OF BULK MATTEREXERCISE - Very short answer questions
163 Videos
- PHYSICAL WORLD AND MEASUREMENTBOOK - PRADEEPCHAPTER - PHYSICAL WORLD AND MEASUREMENTEXERCISE - Competiton Focus Jee Medical Entrance
18 Videos
- RAY OPTICSBOOK - PRADEEPCHAPTER - RAY OPTICSEXERCISE - Problem For Practice(a)
25 Videos
Similar Questions
A bar of mass m and length l is hanging from point A as shown in figure. Find the increase in its length due to its own weight. The young's modulus of elasicity of the wire is Y and area of cross-section of the wire is A.
View SolutionA thick uniform rope of length L is hanging from a rigid support. A transverse wave of wavelength λ0 is set up in the middle of the rope. Te wavelength of the wave as it reaches the top most point is
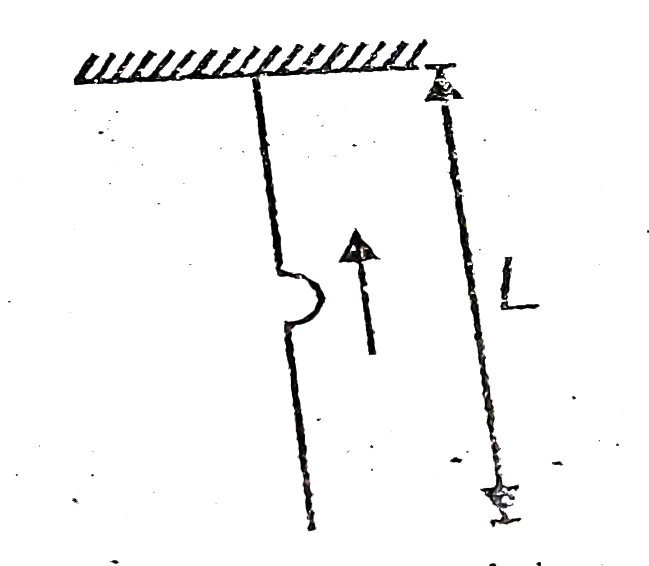
View Solution
Knowledge Check
A rubber rope of length 8 m is hung from the ceiling of a room. What is the increases in length of the rope due to its own weight? (Given, Young's modulus of elasticity of rubber =5×106Nm−2 and density of rubber =1.5×106kgm−3 and g=10ms−2)
A1.5 mmB6 mmC24 mmD96 mmA rubber rope of length 8m is hung from the ceiling of a room. What is the increase in length of rope due to its own weight? (Given: Young's modulus of elasticity of rubber =5×106N/m and density of rubber =1.5×103kg/m3. Take g=10ms−12)
A1.5mmB6mmC24mmD96mmA heavy rope is suspended from the ceiling of a room. If ϕ is the density of the rope, L be its original length and Y be its. Young's modulus, then increase ΔL in the length of the rope due to its own weight is
AΔL=ϕgL2YBΔL=2ϕgL2YCΔL=ϕgL22YDΔL=ϕgLY
A rubber string 10m long is suspended from a rigid support at its one end. Calculate the extension in the string due to its own weight. The density of rubber is 1.5×103 and Young's modulus for the rubber is 5×106Nm−2 Take g=10Nkg−1 .
View SolutionA uniform material rod of length L is rotated in a horizontal plane about a vertical axis through one of its ends. The angular speed of rotation is w. Find increase in length of the rod. It is given that density and Young’s modulus of the rod are r and Y respectively.
View SolutionA stationlay unifrom sting of modlulus Y, density ρ and length 'I' is hanging from a rigid support.
The stress at a distance x from the point of tis suspension.
View SolutionA wire of length L and radius r suspended from rigid support of mass M gm be applied its free end, its elongation is l, then its Young's modulus is
View SolutionA wire of length L and density ρ and Young's modulus Y is hanging from a support. Find the elongation in the length of wire at which wire will break:
View Solution
