A thick straight copper wire, carrying a current of 10 A is bent into a semicircular arc of radius 7.0 cm as a shown in Fig (a). (i) State the direction and calculate the magnitude of magnetic field at the centre of arc. (ii) How would your answer change if the same wire were bent into a semicircular arc of the same radius but in opposite way as shown in Fig. (b)?
A thick straight copper wire, carrying a current of 10 A is bent into a semicircular arc of radius 7.0 cm as a shown in Fig (a). (i) State the direction and calculate the magnitude of magnetic field at the centre of arc. (ii) How would your answer change if the same wire were bent into a semicircular arc of the same radius but in opposite way as shown in Fig. (b)?

Video Solution
Doubtnut Promotions Banner
|
Answer

Step by step video & image solution for A thick straight copper wire, carrying a current of 10 A is bent into a semicircular arc of radius 7.0 cm as a shown in Fig (a). (i) State the direction and calculate the magnitude of magnetic field at the centre of arc. (ii) How would your answer change if the same wire were bent into a semicircular arc of the same radius but in opposite way as shown in Fig. (b)? by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023
Class 12PHYSICSMAGNETIC EFFECTS OF CURRENT

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • A straight wire carrying a current 10A is bent into a semicircular arc of radius 5cm. The magnitude of magnetic field at the center is

    A1.5×10−5T
    B3.14×10−5T
    C6.28×10−5T
    D19.6×10−5T

  • The magnetic field at centre O of the arc in Fig.
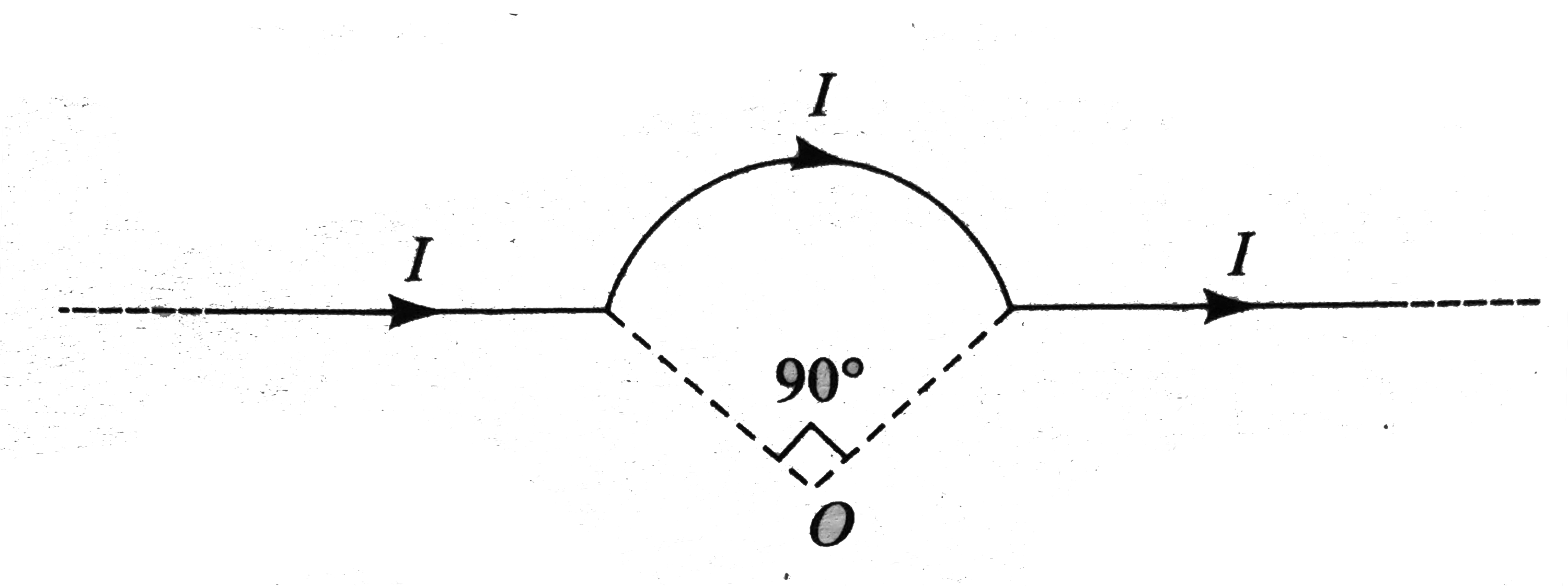    ocr_image

    Aμ0I4π×r[√2+π]
    BμI2πr[π4+(√2−1)]
    Cμ04π×Ir[(√2−π)]
    DμI4π×Ir[√2+π4]

  • A part of a long wire carrying a current i is bent into a circle of radius r as shown in figure. The net magnetic field at the centre O of the circular loop is
    ocr_image

    Aμ0i4r
    Bμ0i2r
    Cμ0i2πr(π+1)
    Dμ0i2πr(π−1)