A thin bar of mass M and length L is free to rotate about a fixed horizontal axis through a point at its end. The bar is brought to a horizontal position and then released. The axis is perpendicular to the rod. The angular velocity when it reaches the lowest point is
directly proportional to its length and inversely proportional to its mass
independent of mass and inversely proportional to the square root of its length
dependent only upon the acceleration due to gravity and the length of the bar
directly proportional to its length and inversely proportional to the acceleration due to gravity
The correct Answer is:B, C, D
Gain in KE=Loss in PE
⇒12Iω2=mgl2⇒12ml23ω2=mgl2
⇒ω=√3gl
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 2Exercise:Multiple Correct
Explore 26 Videos
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 2Exercise:Linked Comprehension
Explore 71 Videos
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 2Exercise:Subjective
Explore 19 Videos
- RIGID BODY DYNAMICS 1Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 1Exercise:Integer
Explore 11 Videos
- SOUND WAVES AND DOPPLER EFFECTBook:CENGAGE PHYSICSChapter:SOUND WAVES AND DOPPLER EFFECTExercise:Integer
Explore 16 Videos
Similar Questions
A rod of mass M and length L lying horizontally is free to rotate about a vertical axis through its end. A horizontal force F on the rod at the other end, the force always remains perpendicular to the rod. Find the angular velocity of the rod when it has turned an angle π/2.
View SolutionA thin uniform rod of mass M and length L is free to rotate in vertical plane about a horizontal axis passing through one of its ends. The rod is released from horizontal position shown in the figure. Calculate the shear stress developed at the centre of the rod immediately after it is released. Cross sectional area of the rod is A. [For calculation of moment of inertia you can treat it to very thin]

View Solution
Knowledge Check
A thin bar of mass m and length l is free to rotate about a fixed horizontal axis through a point at its end. The bar is brought to a horizontal position. (θ=90∘) and then released. The angular velocity when it reaches the lowest point is
Adirectly proportional to its length and inversely proportional to its massBindependent of mass and inversely proportional to the square root of its lengthCdependent only upon the acceleration due to gravity and the mass of the barDdirectly proportional to its length and inversely proportional to its length and inversely proportional to the acceleration due to gravity.A rod of length L is hinged from one end. It is brought to a horizontal position and released. The angular velocity of the rod, when it is in vertical position, is
A√2gLB√3gLC√g2LD√gLA rod of length L is hinged from one end. It is brought to a horizontal position and released. The angular velocity of the rod, When it is in verticle position is
A√2gLB√3gLC√g2LD√gL
A rod of length L is hinged from one end. It is brought to horizontal position and released. The angular velocity of the rod when it is in vertical position. Is
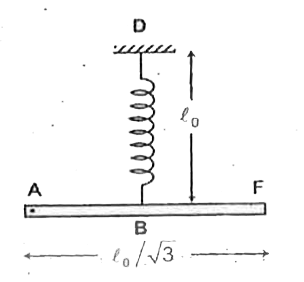
View SolutionIn the figure shown one end of a light spring of natural length l0=√58m(≈0.8m) is fixed at point D and other end is attached to the centre B of a uniform rod AF of length l0/√3 and mass 10kg. The rod is free to rotate in a vertical plane about a fixed horizontal axis passing through the end A of the rod. The rod is held at rest in horizontal position and the spring is in relaxed state. It is found that, when the rod is released to move it makes an angle of 60∘ with the horizontal when it comes to rest for the first time. Find the
(a) the maximum elogation in the spring . (Approximately)
(b) the spring constant. (Approximately)
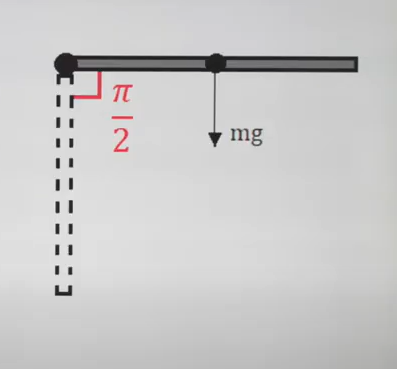
View SolutionA rod is released from the horizontal position as shown. It is free to rotate about hinge. Find angular velocity of rod when it become vertical?
View SolutionA thin uniform rod is free to rotate about a fixed smooth horizontal axis as shown. A point mass hits horizontally with velocity v0 to the one end B of the rod. When it hits, it sticks to the rod, then :

View Solution
A uniform rod of legth L is free to rotate in a vertica plane about a fixed horizontal axis through B. The rod begins rotating from rest. The angular velocity ω at angle θ is given as
View Solution