A thin circular wire of radius R rotatites about its vertical diameter with an angular frequency ω . Show that a small bead on the wire remain at its lowermost point for ω≤√g/R . What is angle made by the radius vector joining the centre to the bead with the vertical downward direction for ω=√2g/R ? Neglect friction.
We have shown that radius joining the bead to the center of the wire mkes an angle θ with the verticle downward direction If N is reaction then as is clear from the figuree
mg=Ncosθ
mrω2=Nsinθ
or m(Rsinθ)ω2=Nsinθ or mRω2=N
From mg=mRω2cosθ or cosθ=gRω2
As cosθ≤1 therefore bead will remain at its lowermost point for
gRω2≤1 , or ω≤√gR
When ω=√2gR
From cosθ=gR(R2g)=12∴θ=60∘
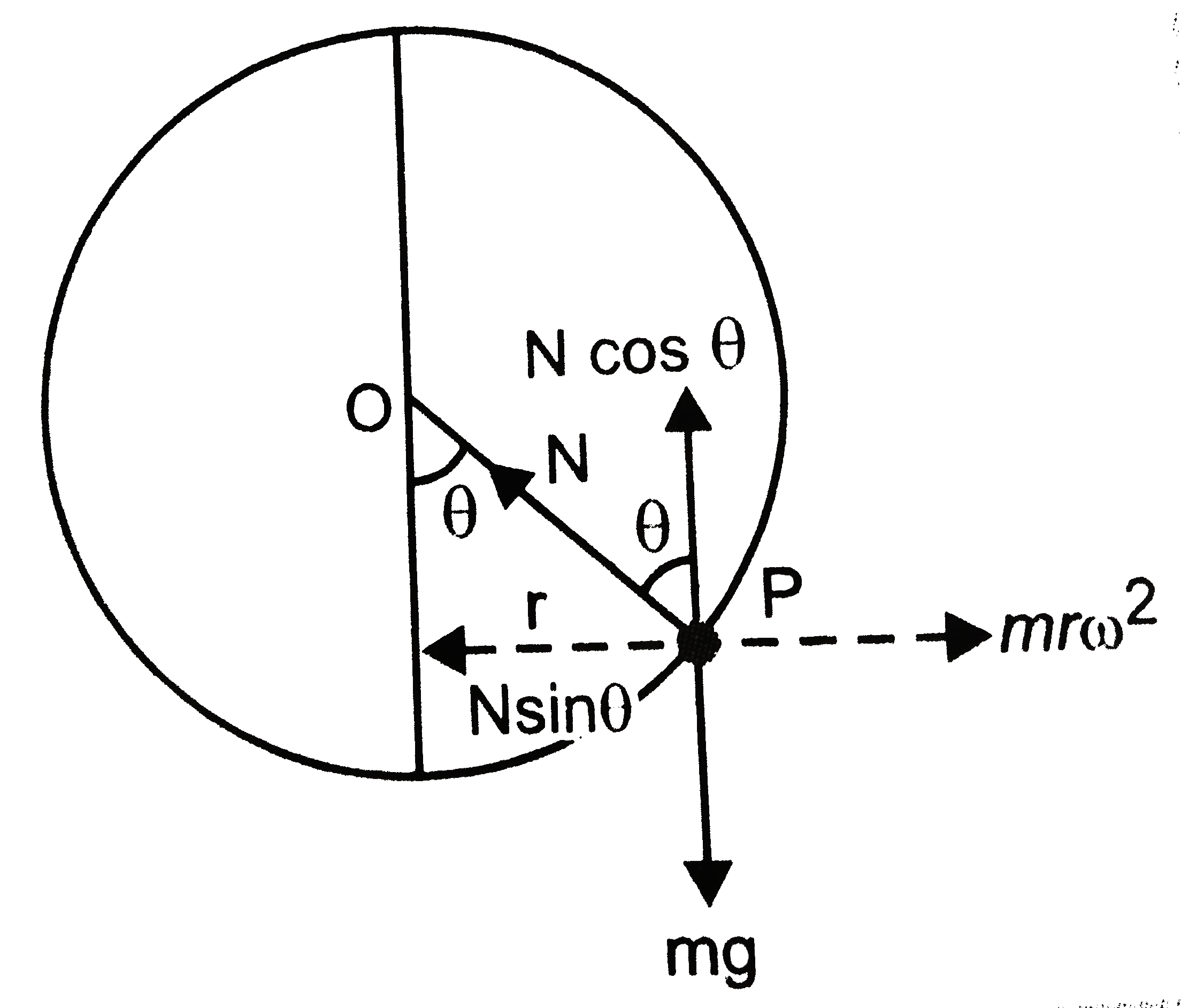 .
.
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - PRADEEPCHAPTER - LAWS OF MOTIONEXERCISE - Additional Examples / Exercises
6 Videos
- LAWS OF MOTIONBOOK - PRADEEPCHAPTER - LAWS OF MOTIONEXERCISE - Short Answer Questions
35 Videos
- LAWS OF MOTIONBOOK - PRADEEPCHAPTER - LAWS OF MOTIONEXERCISE - Advanced problems for competitions
20 Videos
- KINEMATICSBOOK - PRADEEPCHAPTER - KINEMATICSEXERCISE - 1 NCERT Comprehension
4 Videos
- MATHEMATICAL TOOLSBOOK - PRADEEPCHAPTER - MATHEMATICAL TOOLSEXERCISE - Fill in the blanks
5 Videos
Similar Questions
A circular wire of radius r rotates about its own axis with angular speed w in a magnetic field B perpendicular to its plane, then the induced e.m.f. is
View SolutionCalculate the work that has to be done to stop an iron sphere of radius R rotating about its diameter with an angular velocity ω.
View Solution
Knowledge Check
Moment of inertia of a circular wire of mass M and radius R about its diameter is
AMR22BMR2C2MR2DMR24A spherical bowl of radius R rotates about the verical diameter with angular velocity ω.The bowl contains a small object inside and in absence of friction, this object takes up a position inside the bowl such that its radius vector makes an angle θ with the vertical (see figure). Then
 Aω=√g/rcosθBω=2πg/rCω=√gcosθrDω=√rcosθ×g
Aω=√g/rcosθBω=2πg/rCω=√gcosθrDω=√rcosθ×gMoment of inertia of a circular wire of mass M and radius R about its diameter is :
AMR22BMR2C2MR2DMR24
A solid sphere of radius r and mass m rotates about an axis passing through its centre with angular velocity ω. Its K.E. Is
View SolutionA ring of radius r is rotating about a vertical axis along its diameter with constant angular velocity ω.A read of mass m remains at rest w.r.t. ring at the position shown in figure. Then w2 is:
_2019_CBT8_E01_015_Q01.png)
View SolutionIn a uniform magneitc field of induced B a wire in the form of a semicircle of radius r rotates about the diameter of the circle with an angular frequency ω. The axis of rotation is perpendicular to the field. If the total resistance of the circuit is R, the mean power generated per period of rotation is
View SolutionA thin circular ring of mass M and radius R is rotating about its axis with constant angular velocity ω. The objects each of mass m are attached gently to the ring. The wheel now rotates with an angular velocity.
View SolutionA horizontal ring of radius r spins about its axis with an angular velocity ω in a uniform vertical magnetic field of magnitude B. The emf induced in the ring is
View Solution