A thin horizontal circular disc is roating about a vertical axis passing through its centre. An insect is at rest at a point near the rim of the disc. The insect now moves along a diameter of the disc to reach its other end. During the journey of the insect, the angular speed of the disc.
continously decreases
continously increases
first increases and then decreases
remains unchanged
The correct Answer is:C
To solve the problem, we need to analyze the situation involving the rotating disc and the insect moving along its diameter. Here’s a step-by-step breakdown of the solution:
Step 1: Understand the System
We have a thin horizontal circular disc rotating about a vertical axis through its center. An insect is initially at rest at the rim of the disc and then moves towards the center along a diameter.
Hint: Visualize the disc and the insect's path to understand the dynamics involved.
Step 2: Moment of Inertia
The moment of inertia (I) of the disc about its center is given by the formula:
Idisc=12MR2
where M is the mass of the disc and R is its radius. When the insect (mass m) moves, its contribution to the moment of inertia changes based on its distance from the axis of rotation.
Hint: Recall that the moment of inertia depends on the mass distribution relative to the axis of rotation.
Step 3: Total Moment of Inertia
As the insect moves from the rim to the center, the total moment of inertia of the system (disc + insect) can be expressed as:
Itotal=Idisc+mx2
where x is the distance of the insect from the center. As the insect moves towards the center, x decreases.
Hint: Remember that the insect's position affects the total moment of inertia.
Step 4: Conservation of Angular Momentum
Since there is no external torque acting on the system, the angular momentum (L) is conserved:
L=Iω=constant
where ω is the angular speed of the disc.
Hint: Conservation laws are key in rotational dynamics; they help relate changes in moment of inertia to changes in angular speed.
Step 5: Analyze Changes in Angular Speed
As the insect moves towards the center:
- The moment of inertia Itotal decreases because x decreases.
- Since L is constant, if I decreases, ω must increase to keep L constant.
Hint: Think about how a spinning figure skater pulls in their arms to spin faster.
Step 6: Movement Beyond the Center
If the insect were to move back towards the rim after reaching the center, the moment of inertia would increase again, causing the angular speed ω to decrease.
Hint: Consider the reverse scenario when the insect moves outward.
Conclusion
Thus, during the journey of the insect from the rim to the center, the angular speed of the disc first increases and then, if the insect continues moving outward, it would decrease. Therefore, the correct answer is:
Option C: first increases then decreases.
We have a thin horizontal circular disc rotating about a vertical axis through its center. An insect is initially at rest at the rim of the disc and then moves towards the center along a diameter.
The moment of inertia (I) of the disc about its center is given by the formula:
Idisc=12MR2
where M is the mass of the disc and R is its radius. When the insect (mass m) moves, its contribution to the moment of inertia changes based on its distance from the axis of rotation.
As the insect moves from the rim to the center, the total moment of inertia of the system (disc + insect) can be expressed as:
Itotal=Idisc+mx2
where x is the distance of the insect from the center. As the insect moves towards the center, x decreases.
Since there is no external torque acting on the system, the angular momentum (L) is conserved:
L=Iω=constant
where ω is the angular speed of the disc.
As the insect moves towards the center:
- The moment of inertia Itotal decreases because x decreases.
- Since L is constant, if I decreases, ω must increase to keep L constant.
If the insect were to move back towards the rim after reaching the center, the moment of inertia would increase again, causing the angular speed ω to decrease.
Thus, during the journey of the insect from the rim to the center, the angular speed of the disc first increases and then, if the insect continues moving outward, it would decrease. Therefore, the correct answer is:
Option C: first increases then decreases.
Topper's Solved these Questions
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBook:DC PANDEY ENGLISHChapter:SOLVD PAPERS 2017 NEET, AIIMS & JIPMERExercise:Solved paper 2018(JIPMER)
Explore 38 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBook:DC PANDEY ENGLISHChapter:SOLVD PAPERS 2017 NEET, AIIMS & JIPMERExercise:Solved paper 2018(NEET)
Explore 22 Videos
- SIMPLE HARMONIC MOTIONBook:DC PANDEY ENGLISHChapter:SIMPLE HARMONIC MOTIONExercise:Integer type questions
Explore 14 Videos
- SOUND WAVESBook:DC PANDEY ENGLISHChapter:SOUND WAVESExercise:Exercise 19.7
Explore 4 Videos
Similar Questions
A horizontal disc is rotating about a vertical axis passing through its centre. If an insect moves from centre to rim then the angular momentum of the system
View SolutionA disc is free to rotate about a smooth horizontal axis passing through its centre of mass. A particle is fixed at the top of the disc. A slight push is given to the disc and it starts rotating. During the process.

View SolutionThe moment of inertia of a copper disc, rotating about an axis passing through its centre and perpendicular to its plane
View SolutionRadius of gyration of a uniform circular disc about an axis passing through its centre of gravity and perpendicular to its plane is
View SolutionA metallic circular disc having a circular hole at its centre rotates about an axis passing through its centre and perpendicular to its plane. When the disc is heated:
View SolutionA metallic circular disc having a circular hole at its centre rotates about an axis passing through its centre and perpendicular to its plane. When the disc is heated:
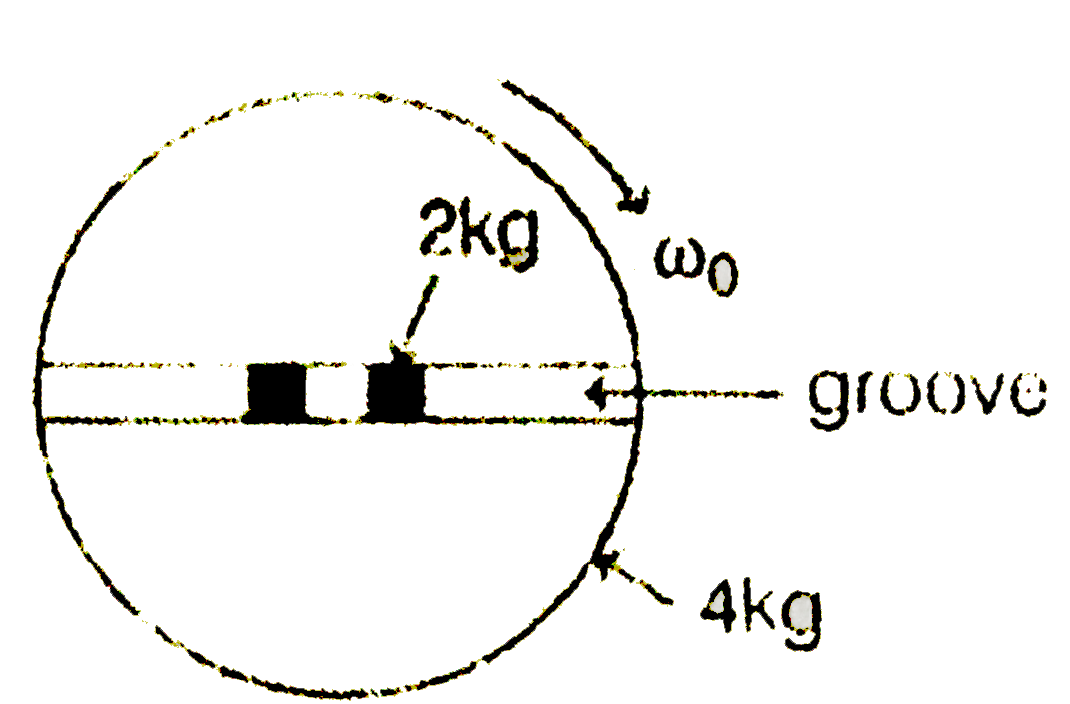
View SolutionA disc of mass 4 kg and radius 6 metre is free to rotate in horizontal plane about a vertical fixed axis passing through its centre. There is a smooth groove along the diameter of the disc and two small blocks of masses 2 kg each are placed in it on either side of the centre of the disc as shown in figure. The disc is given initial angular velocity ω0 =12 rad/sec and released. Find the angular speed of disc (in radian/sec) when the blocks reach the ends of the disc.
View SolutionA nonconducing disc of radius R is rotaing about axis passing through its cente and perpendicual its plance with an agular velocity ω . The magnt moment of this disc is .
View SolutionA uniform disc is rotating at a constantt speed in a vertical plane about a fixed horizontal axis passing through the centre of the disc. A piece of the disc from its rim detaches itself from the disc at the instant when it is at horizontal level with the centre of the disc and moving upward. Then about the fixed axis, the angular speed of the
View SolutionA disc of mass m and radius R is free to rotate in a horizontal plane about a vertical smooth fixed axis passing through its centre. There is a smooth groove along the diameter of the disc and two small balls of mass m/2 each are placed in it on either side of the centre of the disc as shown in Fig. The disc is given an initial angular velocity ω0 and released.

The angular speed of the disc when the balls reach the end of the disc is
View Solution