A thin infinitely long thread carrying a charge λ per unit length is oriented parallel to the infinite conducting plane. The distance between the thread and the plane is equal to l. Find :
(a) the moducles of the vector of the force acting on a unit length of the thread ,
(b) the disribution of surface chagre density σ(x) over the plane, where x is the distance form the plane perpendicular to the conducting surface and passing through the thread.
(a) The force F1 on unit length of the thread is given by
F1=λE1
where E1 is the field at the thread due to image chagre :
E1=−λ2πε0(2l)
Thus F1=−λ24πε0l
minus signs means that the force is one of attraction.
(b) There is an image thread with charge density −λ behind the conducting plane. We calculate the electric field on the counductor. It is
E(x)=En(x)=λlπε0(x2+l2)
on counsidering the thread and its image.
Thus σ(x)=ε0En=λlπ(x2+l2)
Topper's Solved these Questions
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Electric Capacitance - Energy Of An Electric Field46videos
ELECTRODYNAMICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Electric Current72videos
ELECTRODYNAMICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Motion Of Charged Particle In Magnetic Field36videos
ELECTRODYNAMICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRICITY AND MAGNETISMEXERCISE - All Questions6videos
ELECTRICITY AND MAGNETISM
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTROMAGNETISMEXERCISE - All Questions24videos
ELECTROMAGNETISM
Similar Questions
A point charge q is located between two mutually perpendicular conducting half-planes. Its distance from each half-plane is equal to l. Find the modulus of the vector of the force acting on the charge.
View SolutionA long staraight wire is located parallel to an infinite conducting plate at a distance b, The radius of the wire is a Find the capacitance of this system per unit length of the wire under the condition a<<b,
View Solution
Knowledge Check
- Question 1 - Select One
The graph of force per unit legth between two long parallel current carrying conductors and the reciprocal of the distance between them is
Aa parabolaBa circleCa reactangular hyperbolaDa straight line
A thin wire ring of radius R carries a charge q. The ring si oriented parallel to an infinite conducting plane and is spearated by a distance l from it. Find :
(a) the surface chagre density at that point fo the plane symmetrical with respect to the ring,
(b) the strength and the potential of the electric field at the centre of the ring.View SolutionA thread carrying a unifrom charge λ per unit length has the configuration shown in fig, Assuming a curvature radius R to be considerably less than the length of the thread, find the magnitude fo the electric field strength at the point O.
, 
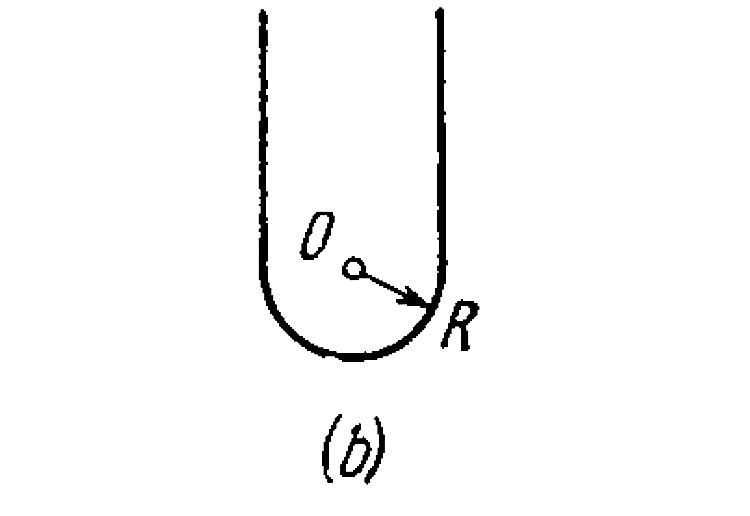View SolutionA point dipole with an electric moment p is located at a distance l from an infinite conducting plane. Find the modulus of the vector of the force acting on the dipoel if the vector p is perpendicular to the plane.
View SolutionThere is infinitely long straight thread carrying a charge with linear density λ.Calculate the potential difference A and B.
View SolutionA long straight wire is located parallel to an infinite conducting plate. The wire is located parallel to an infinite conducting plate. The wire cross-sectional radius is equal to a, the distance between the axis of the wire and the plane equals b. FInd the mutual capacitance of this system per unit length of the wire under the condition a<<b.
View SolutionTwo this parallel threads carry a uniform charge with linear densities lamnda and −λ . The distance between the threads is equal to l. Find the potential of the electric field and the magnitude of its strength vector at the distance r>>l at the angle θ to the vector 1 (fig).
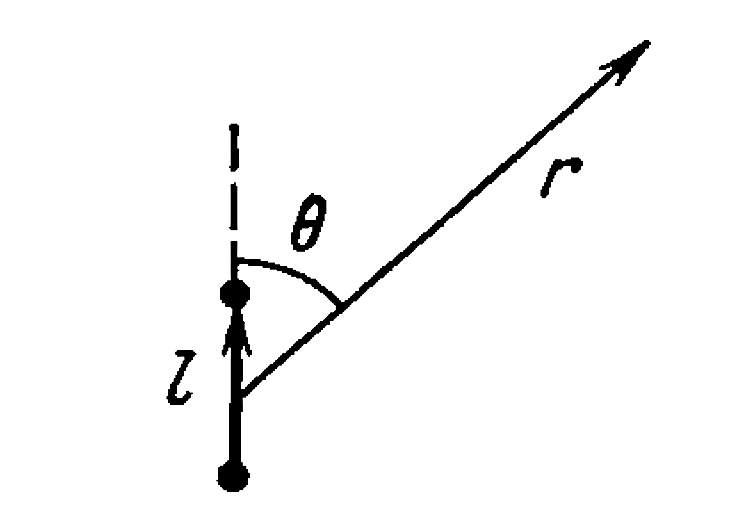View SolutionA very long uniformly thread oriented along the axis of a a circle of raius R rests on its centre with one of the ends. The charge of the thread per unit length is equla to λ. Find the flux of the vector E across the circle area.
View Solution