A thin nonconducting ring of radius R has a linear charge density λ=λ0cosφ, where λ0 is a constant , ϕ is the azimutahl angle. Find the magnitude of the electric field strength
(a) at the centre of the ring ,
(b) on the axis of the ring as a function of the distance x from its centre. Investegation the obtained function at x>>R.
Step by step video solution for A thin nonconducting ring of radius R has a linear charge density lambda = lambda_(0) cos varphi, where lambda_(0) is a constant , phi is the azimutahl angle. Find the magnitude of the electric field strength (a) at the centre of the ring , (b) on the axis of the ring as a function of the distance x from its centre. Investegation the obtained function at x gt gt R. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - ELECTROSTATICSEXERCISE - Partice Exercise 1.11videos
ELECTROSTATICS
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - ELECTROSTATICSEXERCISE - Partice Exercise93videos
ELECTROSTATICS
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTEXERCISE - Advance MCQs33videos
ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENT
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - GEOMETRICAL OPTICSEXERCISE - Unsolved Numerical Problems107videos
GEOMETRICAL OPTICS
Similar Questions
A thin nonconducting ring of radius r has a linear charge density q=q0cosθ, where q0 is a constant and θ is the angle at the centre from the diameter of maximum charge density in the anticlockwise direction. Find the electric field at the centre of the ring.
View SolutionA point charge q is located at the centre fo a thin ring of radius R with uniformly distributed charge −q, find the magnitude of the electric field strength vectro at the point lying on the axis of the ring at a distance x from its centre, if x>>R.
View Solution
Knowledge Check
- Question 1 - Select One
A thin non-conducting ring of radius R has a linear charge density λ=λ0cosθ, where θ is measured as shown. The total electric dipole moment of the charge distribution is
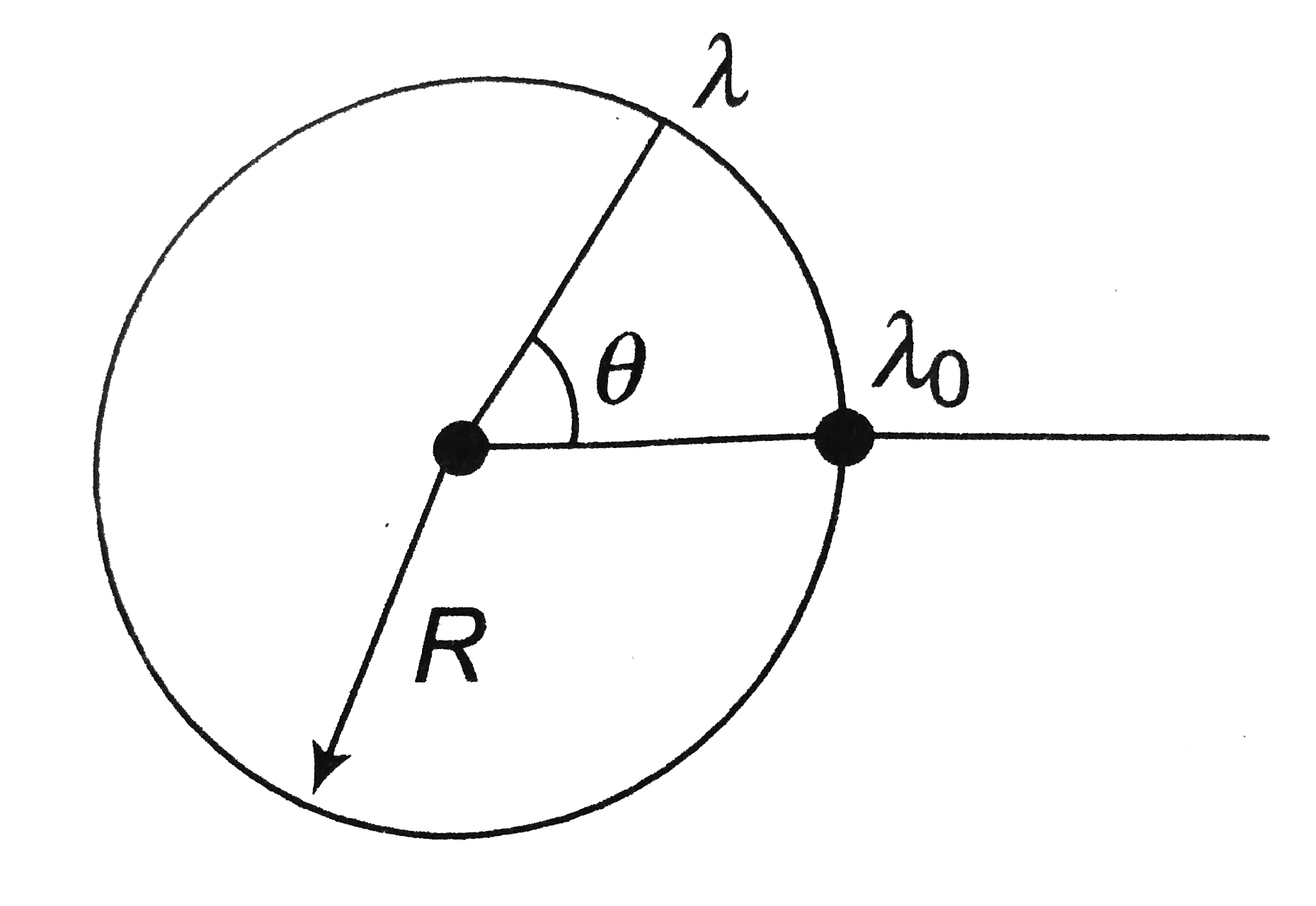 AR2λ0B2πR2λ0CπR2λ02DπR2λ0
AR2λ0B2πR2λ0CπR2λ02DπR2λ0 - Question 2 - Select One
A half ring of radius r has a linear charge density λ.The potential at the centre of the half ring is
Aλ4εoln0Bλ4π2ε0rCλ4πε0rDλ4πε0r2 - Question 3 - Select One
The linear charge density on a ring of radius R is λ=λ0sin(θ) where λ0 is a constant and θ is angle of radius vector of any point on the ring with x-axis. The electric potential at centre of ring is
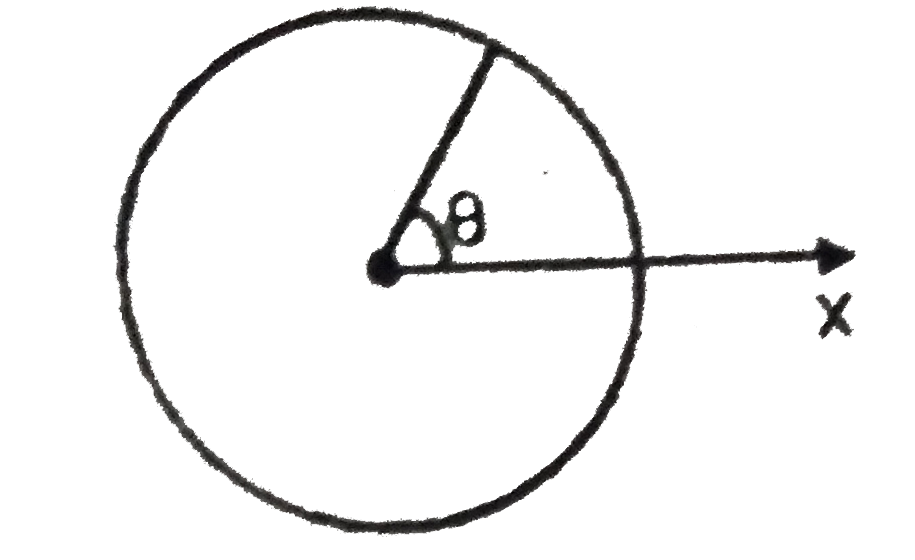 A0Bλ0∈0Cλ0π∈0Dλ02π∈0
A0Bλ0∈0Cλ0π∈0Dλ02π∈0
A thin non-conducting ring or radius a has a linear charge density λ=λ0sinϕ. A uniform electric field E0ˆi+E0ˆj exist in the region . .Net torque acting on ring is given as :
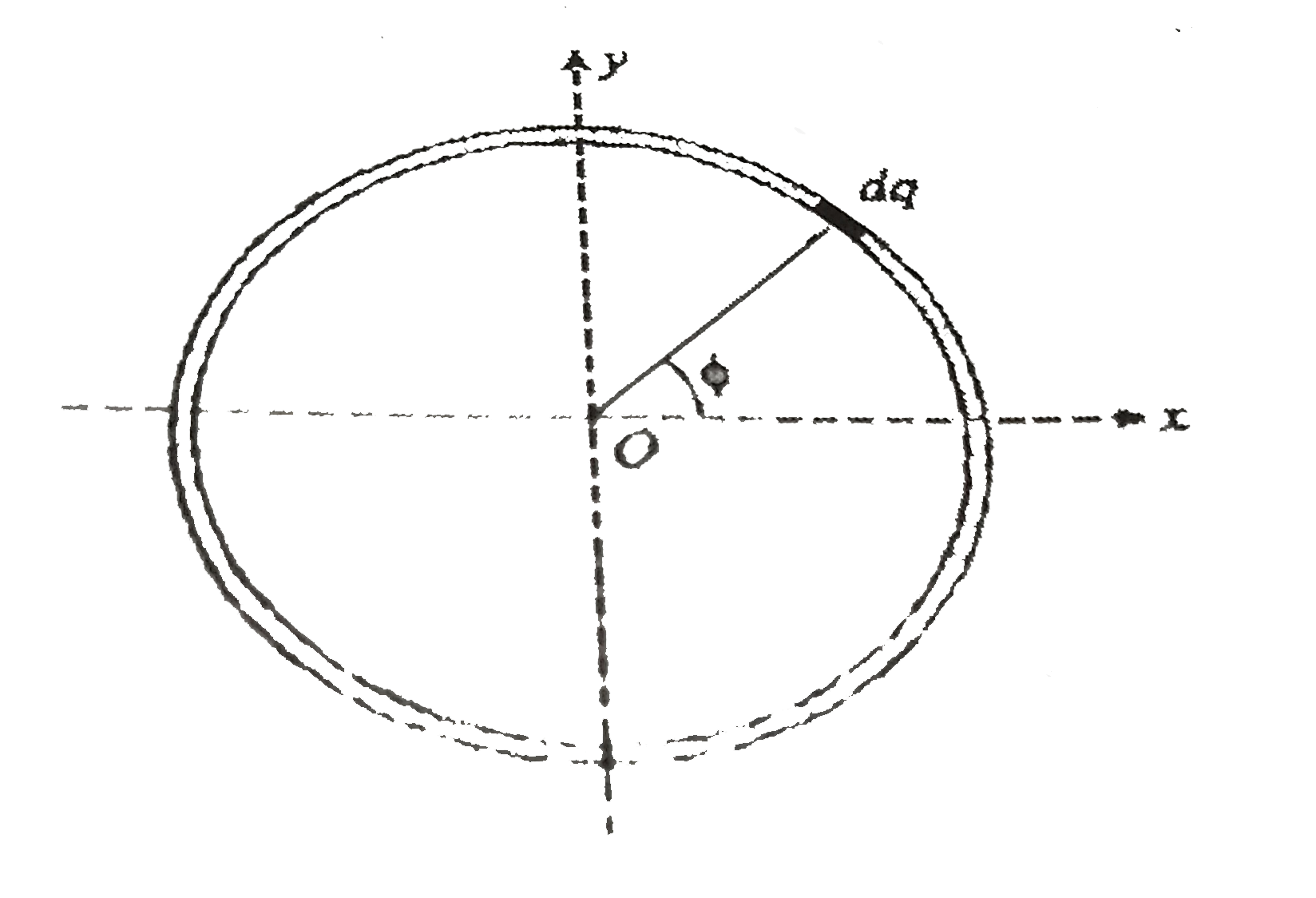 View Solution
View SolutionA thin half- ring of radiusb 20 cm is uniformly charged with a total charge of 0.7nC. Find the magnitude of the electric field at the centre of the centre of the half-ring.
View SolutionA ring has radius 30cm and a charge of 2nC .The electric potential on the axis of the ring at a distance of 40cm from its centre will be
View SolutionA quarter ring of radius R is having uniform charge density λ. Find the electric field and potential at the centre of the ring.
View SolutionThe linear charge density on a dielectric ring of radius R vanes with θ as λ=λ0cosθ/2, where λ0 is constant. Find the potential at the center O of the ring [in volt].
View Solution

