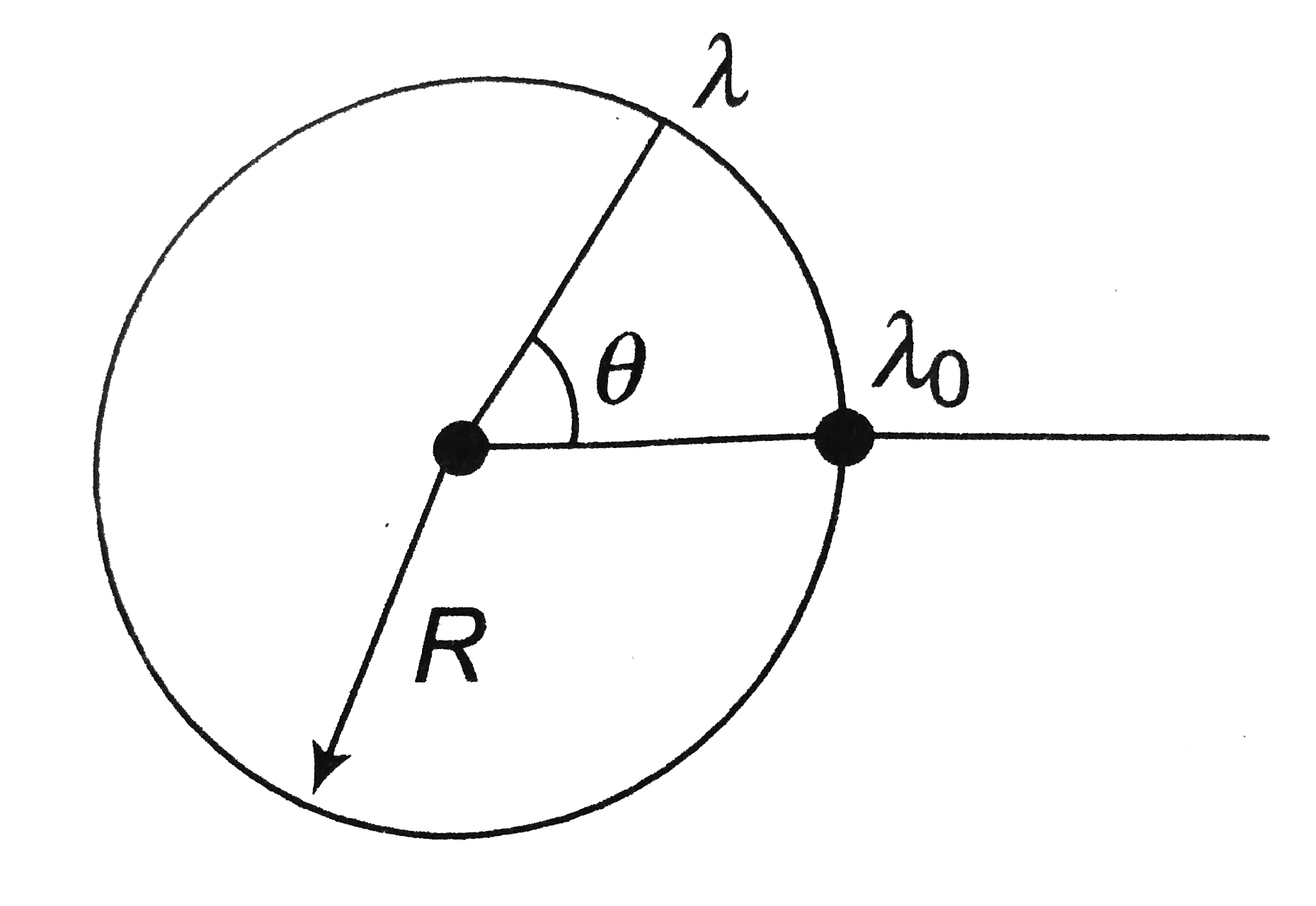
The linear charge density on a dielectric ring of radius R vanes with θ as λ=λ0cosθ/2, where λ0 is constant. Find the potential at the center O of the ring [in volt].
16
0
5
10
The correct Answer is:B
The charge on the infinitesimal elements of arc that subtends an angle dθ at the center of the ring is
dQ=λRdθ=λ0 cos θ2Rdθ
Potential at the center of ring due to charge dQ is
dV=14πε0dQR=λ0 cos θ2Rdθ4πε0R
or V=∫dV=λ04πε02π∫0 cos θ2dθ
=λ04πε0⎡⎣ sin θ212⎤⎦2π0=0V.
 .
.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC POTENTIALEXERCISE - DPP 3.114videos
ELECTRIC POTENTIAL
- BOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC POTENTIALEXERCISE - DPP 3.215videos
ELECTRIC POTENTIAL
- BOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC POTENTIALEXERCISE - Comprehension31videos
ELECTRIC POTENTIAL
- BOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - MCQ s38videos
ELECTRIC FLUX AND GAUSS LAW
- BOOK - CENGAGE PHYSICSCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - M.C.Q2videos
ELECTRICAL MEASURING INSTRUMENTS
Similar Questions
A semi-circular wire is charged with linear charge density dependent on the angle θ from +y -axis as λ=λ0|sinθ|, where λ0 is a constant. The electric field intensity at the center of the arc is ¯¯¯E=mKλ04R(−ˆj). Find m.(R is the radius of semi-circle and K=14πɛ0)
'(##CEN_KSR_PHY_JEE_C18_E01_033_Q18##)'View SolutionA thin nonconducting ring of radius R has a linear charge density λ=λ0cosφ, where λ0 is a constant , ϕ is the azimutahl angle. Find the magnitude of the electric field strength
(a) at the centre of the ring ,
(b) on the axis of the ring as a function of the distance x from its centre. Investegation the obtained function at x>>R.View Solution
Knowledge Check
- Question 1 - Select One
The linear charge density on a ring of radius R is λ=λ0sin(θ) where λ0 is a constant and θ is angle of radius vector of any point on the ring with x-axis. The electric potential at centre of ring is
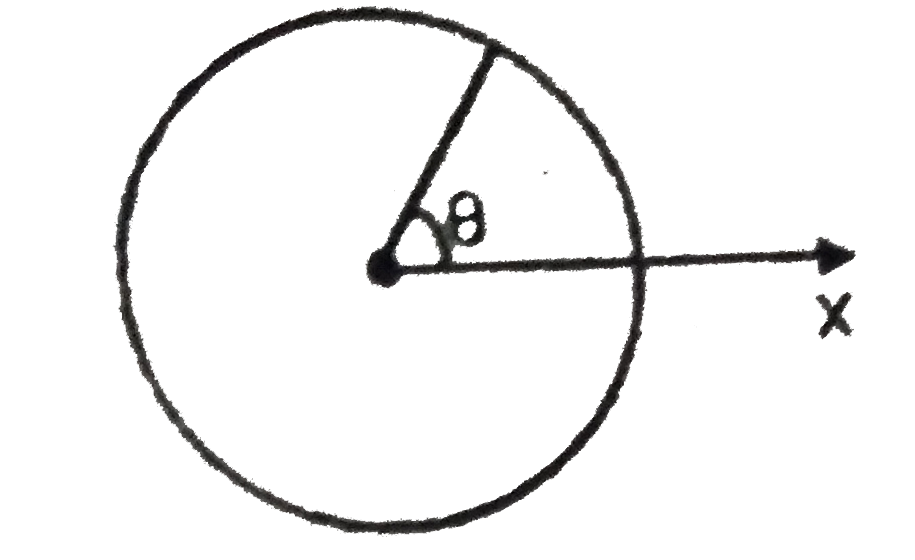 A0Bλ0∈0Cλ0π∈0Dλ02π∈0
A0Bλ0∈0Cλ0π∈0Dλ02π∈0 - Question 2 - Select One
A semicircular wire is uniformly charged with linear charge density dependent on the angle θ from y-direction as λ=λ0|sinθ|, where λ0 is a constant. The electric field intensity at the centre of the arc is
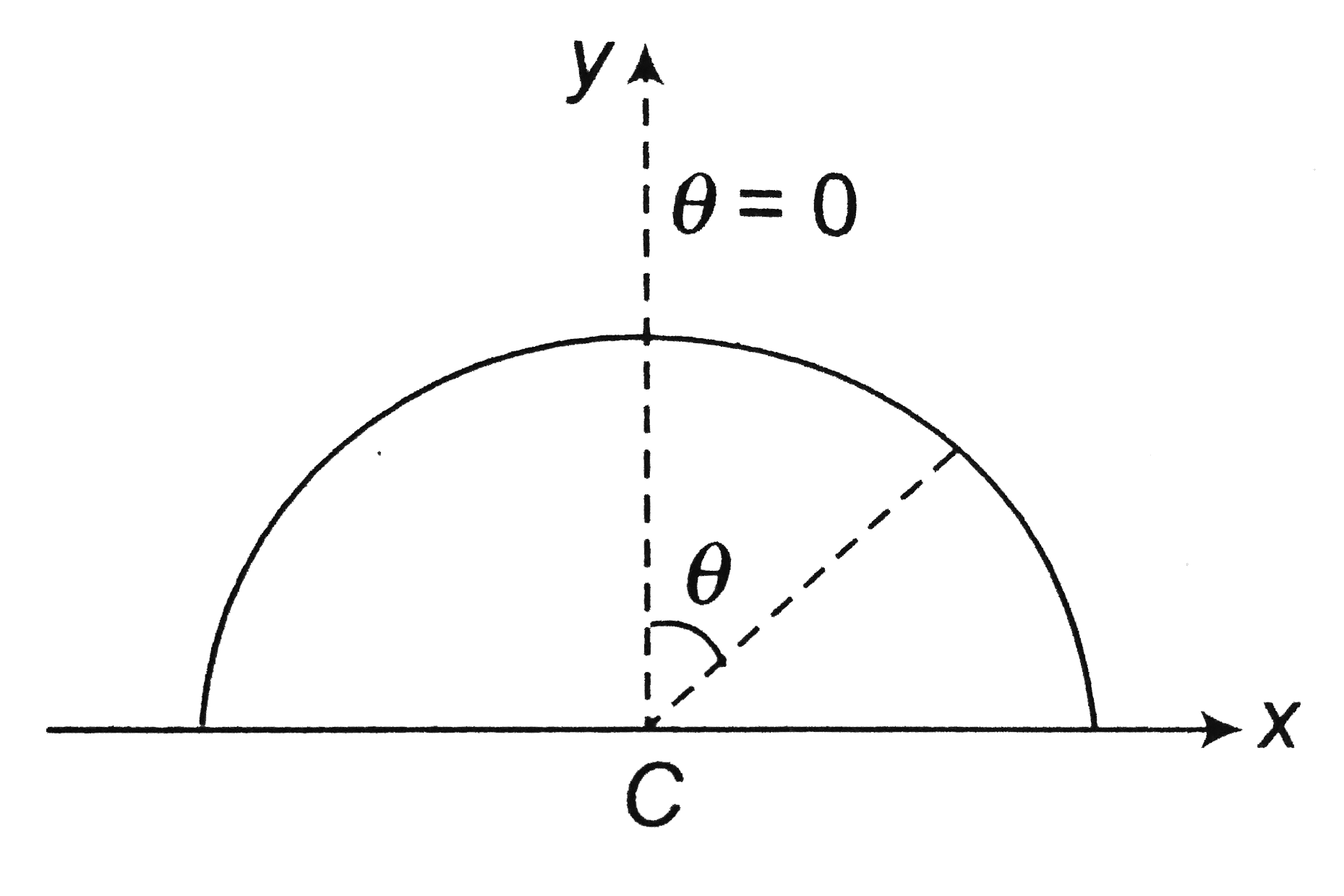 Aλ02πε0R(−ˆj)Bλ04πε0R(−ˆj)Cλ06πε0R(−ˆj)Dλ02√2πε0R(−ˆj)
Aλ02πε0R(−ˆj)Bλ04πε0R(−ˆj)Cλ06πε0R(−ˆj)Dλ02√2πε0R(−ˆj) - Question 3 - Select One
The linear charge density of a uniform semicircular wire varies with θ shown in the figure as λ=λ0cosθ if R is the radius of the loop ,of the charge on the wire is
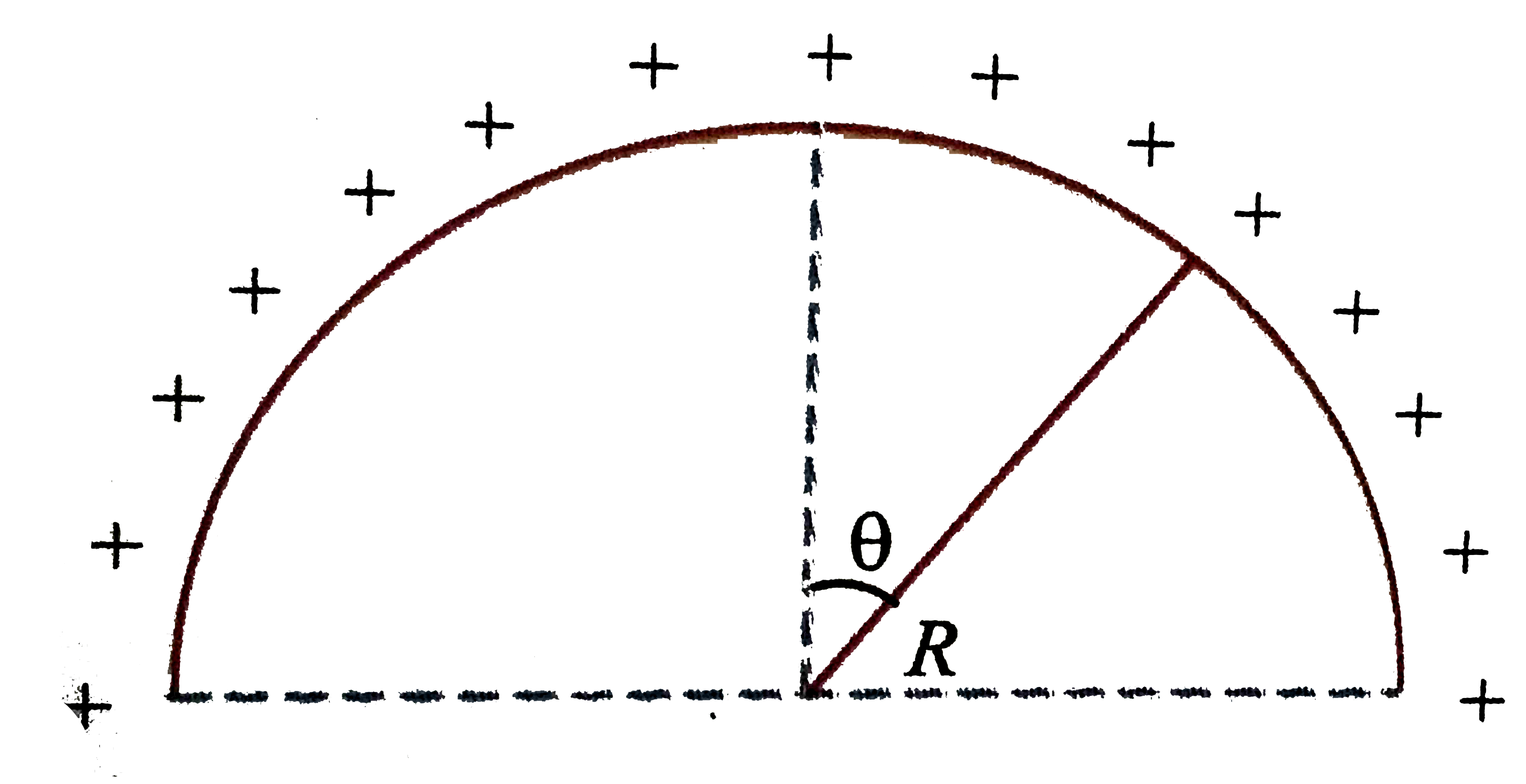 Aλ0RB3λ0RC2λ0R3D2λ0R
Aλ0RB3λ0RC2λ0R3D2λ0R
If linear charge density of a wire of length L depends on distance x from one end as λ=λ0(x)L .Find total charge of wire :-
View Solutionthe linear charge density of a thin metallic rod varies with the distance x from the end as λ=λ0x2(0≤x≤l) The total charge on the rod is
View SolutionA thin non-conducting ring of radius R has a linear charge density λ=λ0cosθ, where θ is measured as shown. The total electric dipole moment of the charge distribution is
 View Solution
View SolutionA half ring of radius r has a linear charge density λ.The potential at the centre of the half ring is
View SolutionA rod with linear charge density λ is bent in the shap of circular ring. The electric potential at the centre of the circular ring is
View Solution

