A thin rod AB is held horizontally so that it can freely rotate in a vertical plane about the end A as shown in the the potential energy of the rod when it hangs vertically is taken to be zero. The end B of the rod is released from rest from a horizontal position. At the instant the rod makes an angle θ with the horizontal,

the speed fo end B is proportional to √sinθ
the potential energy is proportional to (1 - cos θ)
the angular acceleration is proportional to cosθ
the torque about A remains the same as its initial value
The correct Answer is:A, C
Decrease in potential energy of the cnetre of mass of the rod = increase in kinetic energy of the centre of mass of the rod or, mg×AO=12Iω2
[ I = moment of inertia of the rod ]
or, mg×l2 sinθ=12Iω2 or,ω=√sinθ
or, v=√sinθ
Torque, τ=Iω
or, mg×l2cosθ=ml23α or,α=cosθ

Topper's Solved these Questions
- ROTATION OF RIGID BODIES BOOK - CHHAYA PUBLICATIONCHAPTER - ROTATION OF RIGID BODIES EXERCISE - EXAMINATION ARCHIVE with solutions (JEE Main )
10 Videos
- ROTATION OF RIGID BODIES BOOK - CHHAYA PUBLICATIONCHAPTER - ROTATION OF RIGID BODIES EXERCISE - EXAMINATION ARCHIVE with solutions (AIPMT )
3 Videos
- ROTATION OF RIGID BODIES BOOK - CHHAYA PUBLICATIONCHAPTER - ROTATION OF RIGID BODIES EXERCISE - EXAMINATION ARCHIVE with solutions (WBCHSE )
12 Videos
- QUESTION PAPERS OF WBCHSE -2018BOOK - CHHAYA PUBLICATIONCHAPTER - QUESTION PAPERS OF WBCHSE -2018EXERCISE - SECTION -II
20 Videos
- SIMPLE HARMONIC MOTIONBOOK - CHHAYA PUBLICATIONCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - CBSE SCANNER
16 Videos
Similar Questions
Two particles each of mass m are attached at end points of a massless rod AB of length l. Rod is hinged at point C as shown. Rod is released from rest from horizontal position. At the instant when rod reaches its vertical position as shown, which of the following is / are correct:

View SolutionA rod of mass m and length l is himged about one of its ends. The rod is released from horizontal position. When the rod becomes vertical, calculate (i) angular speed of the rod (ii) Hinge reaction.
View Solution
Knowledge Check
Two particles each of mass m are attached at end points of a massless rod AB of length l. Rod is hinged at point C as shown. Rod is released from rest from horizontal position. At the instant when rod reaches its vertical position as shown, which of the following is / are correct:
 ASpeed of the particle at B is thrice the speed of particle at ABNet force on particle B is 6mg5CAngular acceleration of the system is zero.DBoth x and y components of hinge force are non-zero
ASpeed of the particle at B is thrice the speed of particle at ABNet force on particle B is 6mg5CAngular acceleration of the system is zero.DBoth x and y components of hinge force are non-zero
In the figure shown one end of a light spring of natural length l0=√58m(≈0.8m) is fixed at point D and other end is attached to the centre B of a uniform rod AF of length l0/√3 and mass 10kg. The rod is free to rotate in a vertical plane about a fixed horizontal axis passing through the end A of the rod. The rod is held at rest in horizontal position and the spring is in relaxed state. It is found that, when the rod is released to move it makes an angle of 60∘ with the horizontal when it comes to rest for the first time. Find the
(a) the maximum elogation in the spring . (Approximately)
(b) the spring constant. (Approximately)
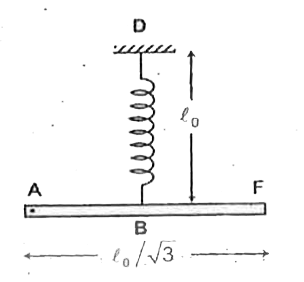
View SolutionIn the figure shown one end of a light spring of natural length l0=√58m(≈0.8m) is fixed at point D and other end is attached to the centre B of a uniform rod AF of length l0/√3 and mass 10kg. The rod is free to rotate in a vertical plane about a fixed horizontal axis passing through the end A of the rod. The rod is held at rest in horizontal position and the spring is in relaxed state. It is found that, when the rod is released to move it makes an angle of 60∘ with the horizontal when it comes to rest for the first time. Find the
(a) the maximum elogation in the spring . (Approximately)
(b) the spring constant. (Approximately)

View SolutionA thin rod MN free to rotation in the vertical plane about the fixed end N is held horizontal when the end M is released the speed of this end when the rod makes an angle α with the horizontal will be proportional to : (see figure)

View SolutionA thin rod MN free to rotation in the vertical plane about the fixed end N is held horizontal when the end M is released the speed of this end when the rod makes an angle α with the horizontal will be proportional to : (see figure)

View SolutionA rod of length l is pivoted about a horizontal , frictionless pin through one end. The rod is released from ret in a vertical position. Find the velocity of the CM of the rod when the rod is inclined at an angle θ from the vertical.

View SolutionA rod of length l is pivoted about a horizontal , frictionless pin through one end. The rod is released from ret in a vertical position. Find the velocity of the CM of the rod when the rod is inclined at an angle θ from the vertical.

View SolutionA rod of length l is released from the vertical position on a smooth horizontal plane. What is the nature of motion of the free end of the rod ?
View Solution
