A thin rod of mass 0.9 kg and length 1 m is suspended , at rest form one end so that it can freely oscillate in the vertical plane. A particle of move 0.1 kg moving in a striaght line with velcoity 80 n/s hits the rod at is bottom most point and sticks to it (see figure) . The angluar speed ( in rad/s) of the rod immediately after the collision will be .
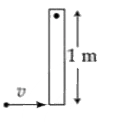
Step by step video & image solution for A thin rod of mass 0.9 kg and length 1 m is suspended , at rest form one end so that it can freely oscillate in the vertical plane. A particle of move 0.1 kg moving in a striaght line with velcoity 80 n/s hits the rod at is bottom most point and sticks to it (see figure) . The angluar speed ( in rad/s) of the rod immediately after the collision will be . by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A uniform rod of mass 2 kg and length 1 m lies on a smooth horizontal plane. A particle of mass 1 kg moving at a speed of 2m/s perependicular to the length of the rod strikes it at a distance 14 m from the centre and stops . Find the angular velocity of the rod about its centre just after the collision (in rad/s)
View SolutionA rod of mass 12 m and length l lying on a smooth horizontal plane can rotate freely about a stationary, vertical axis passing through the rod's end. A particle of mass m moving along the plane with speed v0 hits the rod's end perpendicularly and gets stuck there. Find the angular velocity of the system.

View Solution
Knowledge Check
A thin rod of length 1 m is suspended from its end and is made to oscillate in a vertical plane. The distance between the point of suspension and centre of oscillation will be :
A12mB34mC1 mD23mA uniform rod of mass 20 Kg and length 1.6 m is piovted at its end and swings freely in the vertical plane. Angular acceleration of the rod just after the rod is relased from rest in the horizontal position is
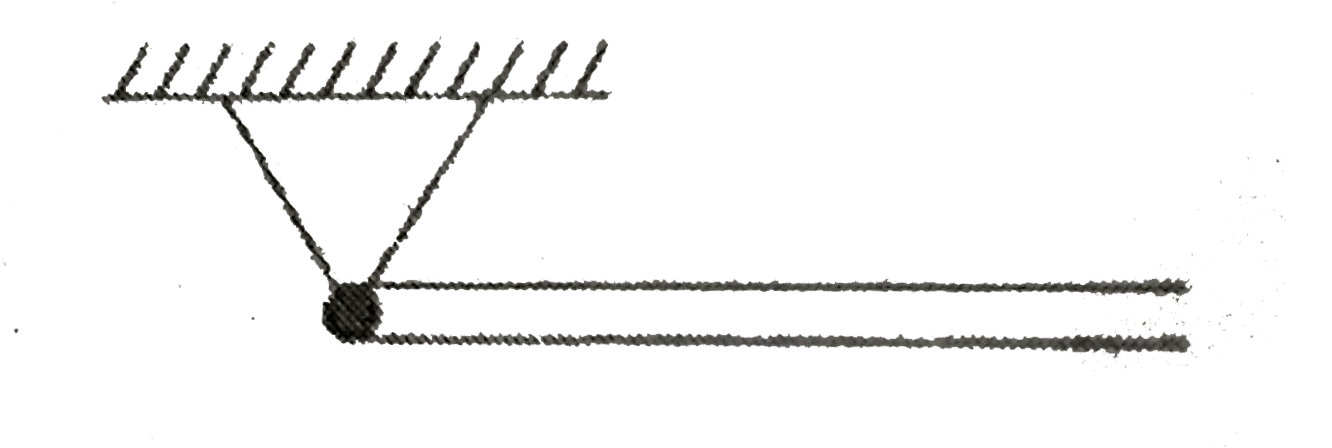 A15g16B17g16C16g15Dg15
A15g16B17g16C16g15Dg15Rod of m and length l is free to rotate about point U in vertical plane. A particle having same mass m moving horizontally with velocity v0 his the rod perpendicular at distance l4 from the top end 'O' and stops. Find impulse due to hinge on the rod due to collision.
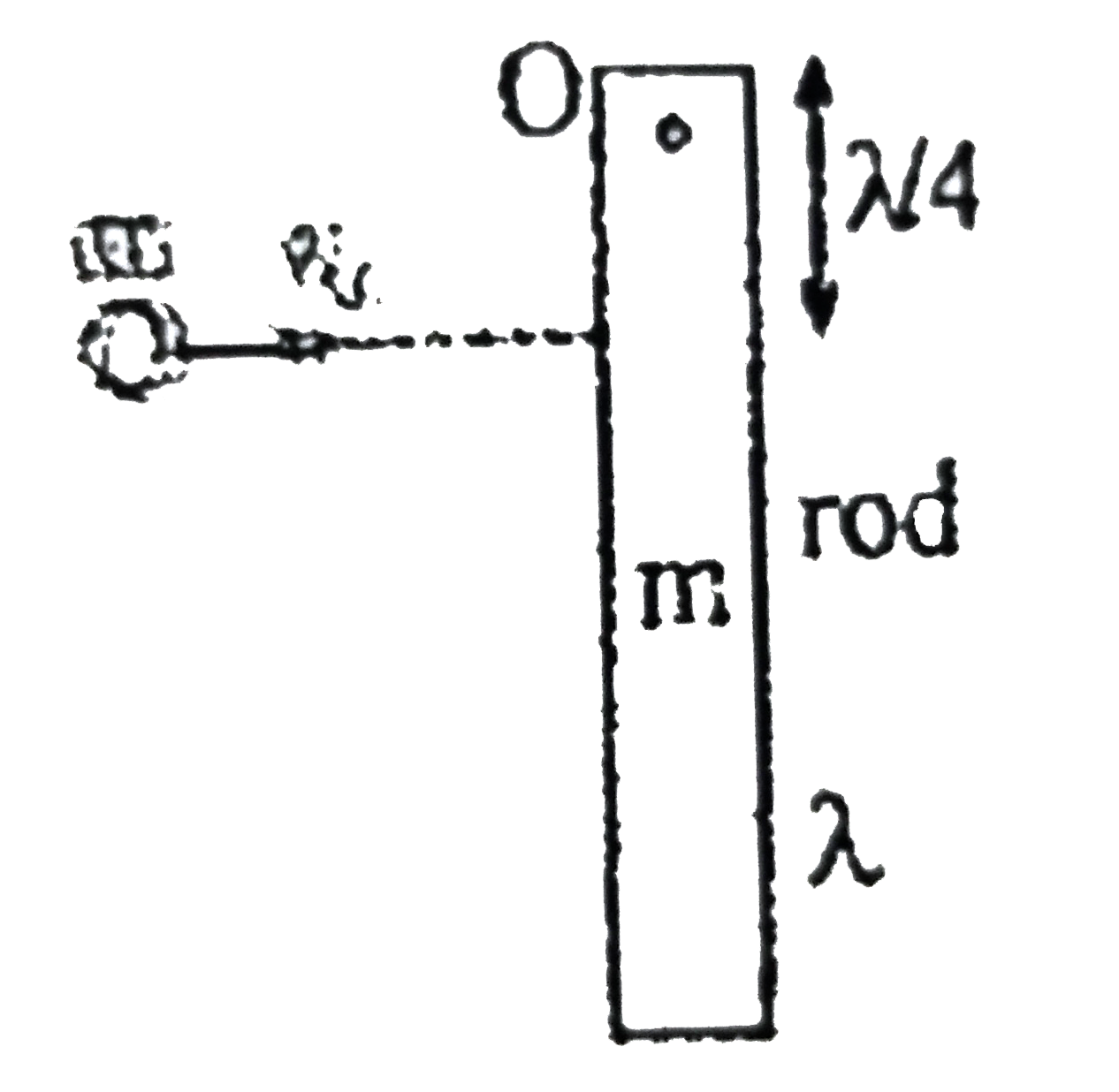 Amv019B−10mv019Cmv0D5mv08
Amv019B−10mv019Cmv0D5mv08
A uniform rod of mass m and length l is hinged at upper end. Rod is free to rotate in vertical plane. A bail of mass m moving horizontally with velocity v0 collides at lower end of rod perpendicular to it and sticks to it. The minimum velocity of the ball such that combined system just completes the vertical circle will be
View SolutionA uniform rod is resting freely over a smooth horizontal plane. A particle moving horizontally strikes at one end of the rod normally and gets stuck. Then
View SolutionConsider a rod of mass M and length L pivoted at its centre is free to rotate in a vertical position plane. The rod is at rest in the vertical position. A bullet of mass M moving horizontally at a speed v strikes and embedded in one end of the rod. The angular velocity of the rod just after the collision will be.
View SolutionA uniform rod of mass m and length L is at rest on a smooth horizontal surface. A ball of mass m, moving with velocity v0, hits the rod perpendicularly at its one end and sticks to it. The angular velocity of rod after collision is

View SolutionA unifrom rod of mass m and length l0 is pivoted at one end and is hanging in the vertical at one end and is hagingh in the vertical direction.The period of small angular oscillations of the rod is

View Solution
