A thin spherical shell radius of R has a charge Q uniformly distributed on it. At the centre of the shell, a negative point charge -q is placed. If the shell is cut into two identical hemispheres, still equilibrium is maintained. Then find the relation between Q and q?

Here the outward electric pressure at every point on the shell due to its own charge is
Due to -q, the electric field on the surface of the shell is
This electric field pulls every point of the shell in inward direction. The inward pressure on the surface of the shell due to the negative charge is
For equilibrium of the hemispherical shells
or
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDSBOOK - AAKASH SERIESCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Assess Your Self
13 Videos
- ELECTRIC CHARGES AND FIELDSBOOK - AAKASH SERIESCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Exercise-I
80 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - AAKASH SERIESCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - PRACTICE EXERCISEX
42 Videos
- ELECTRIC FIELD AND POTENTIALBOOK - AAKASH SERIESCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - PROBLEMS (LEVEL-II)
26 Videos
Similar Questions
A thin spherical conducting shell of radius R has a charge q. Another charge Q is placed at the centre of the shell. The electrostatic potential at a point P a distance R2 from the centre of the shell is
View SolutionA thin spherical conducting shell of radius R has a charge q. Another charge Q is placed at the centre of the shell. The electrostatic potential at a point P a distance R/2 from the centre of the shell is
View SolutionA positive charge Q is uniformly distributed along a circular ring of radius R.a small test charge q is placed at the centre of the ring.

View SolutionA spherical shell of radius R carries a uniformly distributed charge q. The electrical forces arising cause the ex-pansion of the shell. Find the mechanical stress in the shell.
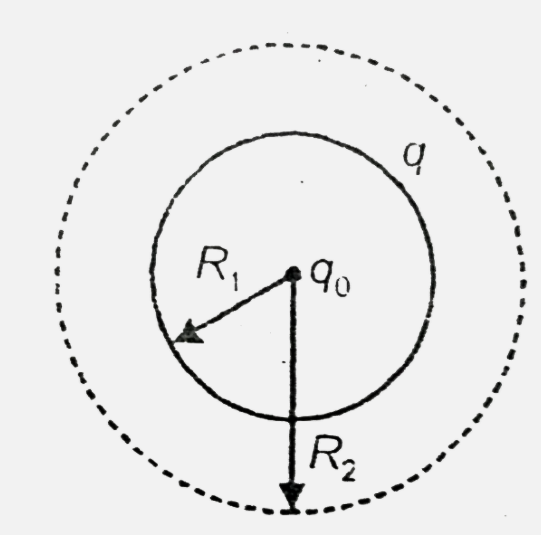
View SolutionA sperical shell is uniformly charged by a charge q. A point charge q0 is at its centre , then
View SolutionA spherical shell having charge +Q (uniformly distributed) and a point charge +q0 are placed as shown. Find the force between shell and the point charge (r>>R).
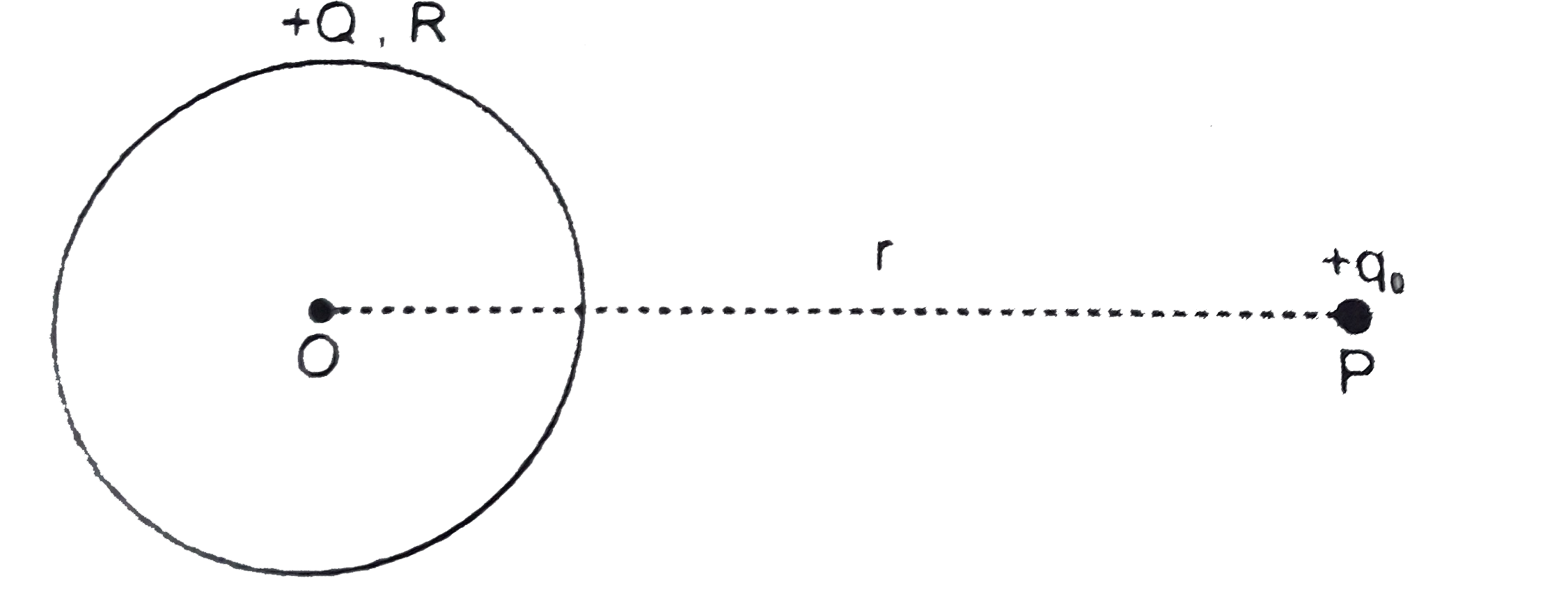
View SolutionA thin metallic spherical shell contains a charge Q on it. A point charge q is placed at the center of the shell and another charge q1 is placed outside it as shown in the figure. All the three charges are positive. Find the force on the charge

a. at centre due to all charges.
b. at center due to shell.
View SolutionA thin. Metallic spherical shell contains charge Q on it. A point charge q is placed at the centre of the shell and another charge q1 is placed outside it as shown in figure . All the three charges are positive. The force on the charge at the centre is

View SolutionA thin circular wire of radius r has a charge Q. If a point charge q is placed at the centre of the ring, then find the increase in tension in the wire.
View SolutionA thin metallic spherical shell carries a charge Q on it. A point charge Q1 is placed at the centre of the shell and another charge q is placed outside as shown in figure ahead. All the charges are positive . Discuss the various forces acting on Q1.

View Solution
