A thin square steel plate 10 cm on a side is heated in a black smith's forge to temperature of 800∘C. If the emissivity is 0.60, what is the total rate of radiation of energy ?
To find the total rate of radiation of energy from the thin square steel plate, we can use Stefan-Boltzmann Law, which states that the power radiated by a black body is proportional to the fourth power of its absolute temperature. The formula for the power radiated is given by:
P=σ⋅E⋅A⋅T4
Where:
- P = total power radiated (in watts)
- σ = Stefan-Boltzmann constant ≈5.67×10−8W/m2K4
- E = emissivity of the material (dimensionless)
- A = surface area of the plate (in m²)
- T = absolute temperature in Kelvin (K)
Step 1: Convert the temperature from Celsius to Kelvin
The temperature given is 800∘C. To convert this to Kelvin, we use the formula:
T(K)=T(°C)+273.15
So,
T=800+273.15=1073.15K
Step 2: Calculate the area of the square plate
The side of the square plate is given as 10 cm. We need to convert this to meters:
Side=10cm=0.1m
The area A of the square plate is given by:
A=side2=(0.1m)2=0.01m2
Step 3: Substitute values into the Stefan-Boltzmann Law
Now we can substitute the values into the formula:
P=σ⋅E⋅A⋅T4
Substituting the known values:
- σ=5.67×10−8W/m2K4
- E=0.60
- A=0.01m2
- T=1073.15K
So,
P=5.67×10−8⋅0.60⋅0.01⋅(1073.15)4
Step 4: Calculate T4
Calculating T4:
T4=(1073.15)4≈1.307×1012K4
Step 5: Calculate the total power radiated
Now substituting T4 back into the equation:
P=5.67×10−8⋅0.60⋅0.01⋅1.307×1012
Calculating this gives:
P≈5.67×10−8⋅0.60⋅0.01⋅1.307×1012≈445.2W
Final Answer
The total rate of radiation of energy from the plate is approximately 445.2 watts.
---
- P = total power radiated (in watts)
- σ = Stefan-Boltzmann constant ≈5.67×10−8W/m2K4
- E = emissivity of the material (dimensionless)
- A = surface area of the plate (in m²)
- T = absolute temperature in Kelvin (K)
The temperature given is 800∘C. To convert this to Kelvin, we use the formula:
The side of the square plate is given as 10 cm. We need to convert this to meters:
Now we can substitute the values into the formula:
- E=0.60
- A=0.01m2
- T=1073.15K
Calculating T4:
Now substituting T4 back into the equation:
The total rate of radiation of energy from the plate is approximately 445.2 watts.
Topper's Solved these Questions
- CALORIMETRY & HEAT TRANSFERBOOK - DC PANDEYCHAPTER - CALORIMETRY & HEAT TRANSFEREXERCISE - Level 2 Single Correct
7 Videos
- CALORIMETRY & HEAT TRANSFERBOOK - DC PANDEYCHAPTER - CALORIMETRY & HEAT TRANSFEREXERCISE - Level 2 More Than One Correct
5 Videos
- CALORIMETRY & HEAT TRANSFERBOOK - DC PANDEYCHAPTER - CALORIMETRY & HEAT TRANSFEREXERCISE - Level 1 Objective
11 Videos
- BASIC MATHEMATICSBOOK - DC PANDEYCHAPTER - BASIC MATHEMATICSEXERCISE - Exercise
13 Videos
- CALORIMETRY AND HEAT TRANSFERBOOK - DC PANDEYCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Medical entrance s gallery
38 Videos
Similar Questions
A copper ball 2 cm in radius is heated in a furnace at 327∘C If its emissivity is 0.3, at what rate does it radiate energy ?
View SolutionUnlike most other plants, a special type of cabbage called skunk cabbage can regulate its internal temperature ( set at T = 22∘C )by altering the rate at which it produces energy. If it becomes covered with snow, it can increase that its thermal radiation metls the snow in order to re-expose the plant to sunlight. Let's model a skunk cabbage with a cylinder of height h = 5.0 cm and radius R = 1.5 cm and assume it is surrounded by a snow wall at temperature Tenv=−3.0∘C (Figure) . If the emissivity ε is 0.80, what is the net rate of energy exchange via thermal radiation between the plant's curved side and the snow ?

View Solution
Knowledge Check
A thin square steel plate with each side equal to 10 cm is heated by a blacksmith. The rate of radiated energy by the heated plate is 1134 W . The temperature of the hot steel plate is (Stefan's constant σ=5.67×10−8 watt m−2K−4 , emissivity of the plate = 1)
A1000 KB1189 KC2000 KD2378 KThe temperature of the sun is 6000 K and is treated as a black body. The solar heat energy radiated by the sun is 109W/m2. What is the temperature of a black body if it radiated heat energy of 105W/m2 ?
A227∘CB27∘CC327∘CD400∘CConsider a black body radiation in a cubical box at absolute temperature T. If the lengh of each side of the box is doubled and the temperature of the walls of the box and that of the radiation is halved then the total energy
AhalvesBdoublesCquadruplesDremains constant
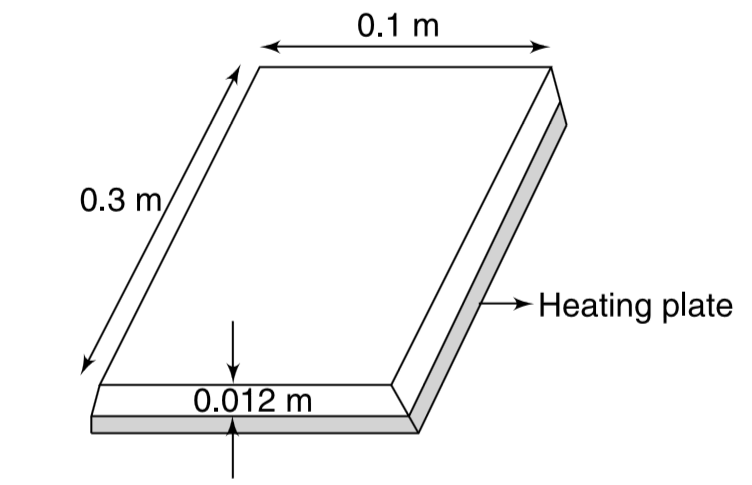
A steel plate is 0.3m long, 0.1m wide and 0.012m thick. The plate is placed on a heating plate of identical size maintained at 100∘C. The heating plate is receiving energy through a 50 W heater. The heating plate losses heat only to the steel plate which is well insulated from all sides except at the top. The top surface of the steel plate is exposed to an airstream of temperature 20∘C. The top surface of the steel plate radiates like a black body. Calculate the rate at which the top surface looses heat due to convection. The surface of steel plate in contact with heating plate is at 100∘C. Thermal conductivity of steel k=16Wm−1K−1 Stefan’s constant =5.67×10−8Wm−2K−4
View SolutionAn electric stove burner of diameter 20cm is at a temperature of 250∘C. If σ=5.67×10−8W/m2.K4, at what rate is the burner radiating energy ? Assume the emissivity ε=0.6.
View SolutionThe rate of dissipation of heat by a black body at temperature T is Q. What will be the the rate of dissipation of heat by another body at temperature 2T and emissivity 0.25?
View SolutionA black body maintained at a certain temperature radiates heat energy at the rate Q watt. If its surface is smoothened so as to lower its emissivitiy by 10%, what will be the increase in its rate of radiation at double the initial temperature?
View SolutionIf the temperature of a black body incresese from 7∘C to 287∘C then the rate of energy radiation increases by
View Solution