A thin tube of uniform cross-section is sealed at both ends. It lies horizontally, the middle 5 cm containing mercury and the two equal end containing air at the same pressure P. When the tube is held at an angle of 60∘ with the vetical direction, the length of the air column above and below the mercury column are 46 cm and 44.5 cm respectively. Calculate the pressure P in centimeters of mercury. (The temperature of the system is kept at 30∘C).
75.4
45.8
67.5
89.3
The correct Answer is:A
Let a be the area of cross-section of the tube. When the tube is horizontal, the 5 cm column of Hg is in the middle, so length of air column on either side at pressure P=46+44.52=45.25cm
When the rube is held at 60∘ with the vertical, the lengths of air columns at the bottom and the top are 44.5 cm and 46 cm respectively. If P1andP2 are their pressures. then
P1−P25cos60∘=5×12=52 cm of Hg
Using Boyle's law for constant temperature,
PV=P1V1=P2V2
P×A×45.25=P1×A×44.5=P2×A46
∴P×45.2544.5−P×45.2546=52
orP5×44.5×462×45.25×1.5=75.4 cm of Hg
Topper's Solved these Questions
- KINETIC THEORYBOOK - NCERT FINGERTPS ENGLISHCHAPTER - KINETIC THEORYEXERCISE - EXEMPLAR PROBLEMS
8 Videos
- KINETIC THEORYBOOK - NCERT FINGERTPS ENGLISHCHAPTER - KINETIC THEORYEXERCISE - ASSERTION & REASON
10 Videos
- KINETIC THEORYBOOK - NCERT FINGERTPS ENGLISHCHAPTER - KINETIC THEORYEXERCISE - SPECIFIC CEAT CAPACITY
13 Videos
- GRAVITATIONBOOK - NCERT FINGERTPS ENGLISHCHAPTER - GRAVITATIONEXERCISE - Assertion And Reason
15 Videos
- LAWS OF MOTIONBOOK - NCERT FINGERTPS ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Assertion And Reason
15 Videos
Similar Questions
A thin tube of uniform cross section is sealed at both ends. It lies horizontally, the middle 5cm containing mercury and the parts on its two sides containing air at the same pressure p. when the tube is held at and angle of 60∘ with the vertical, the length of the air column above and belw the mercury pellet are 46cm and 44.5cm respectively. Calculate the ressure - in centimeters of mercury, The timperature of the system is kept at 30∘C.
View SolutionA thin tube of uniform cross section is sealed at both ends. It lies horizontally. The middle 5 cm containing Hg and the two equal parts containing air at the pressure P0.When the tube is held at an angle 60∘ with the vertical, the length of air column above and below the mercury are 46 and 44.5 cm respectively. Calculate the pressure P0 in cm of Hg (the temperature of the system is kept at 30∘C).
View Solution
Knowledge Check
What will be the length of mercury column in a barometer tube when the atmospheric pressure is x cm of mercury and the tube is inclined at an angle ϕ with the vertical direction ?
AxsinϕBxcosϕCxtanϕDx
A thin tube, sealed at both ends, is 100cm long. If lies horizontally, the middle 10cm containing mercury and the two equal containing air at stan-dard atmospheric pressure. If the tube is now turned to a verical position, by what amount will the mercury be displaced ?
View SolutionA thin tube sealed at both ends is 90 cm long. It is kept horizontally, the middle 10cm containing mercury and the two equal ends containing air at standard atmospheric pressure. The tube is turned and kept in vertical position. By what amount will the mercury be displaced?
View SolutionA barometer tube is inclined at an angle of 30∘ with horizontal direction. Calculate length of mercury column in tube if atmospheric pressure is 76 cm of mercury.
View SolutionWhat will be the length of mercury column in a barometer tube when the atmosperic pressure is 75cm of mercury and the tube is inclined at an angle of 60∘ with the horizontal direction?
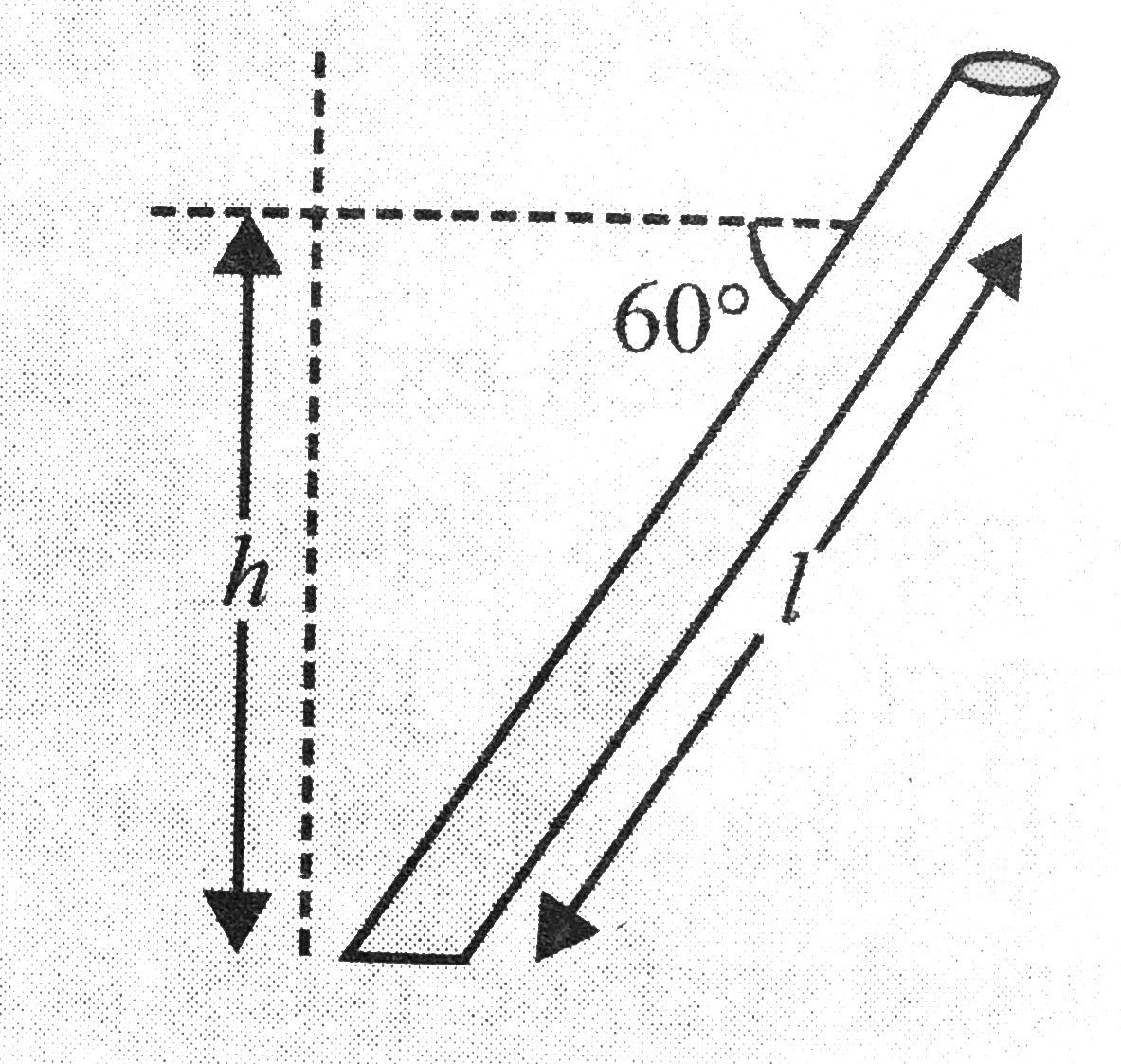
View SolutionA glass tube sealed at both ends is 100cm long, It lies horizontally with the middle 10cm containing mercury. The two ends of the tube contain air at 27∘Cand at a pressure 76cm of mercury. The air column on one side is maintained at 0∘Cand the other side is maintained at 127∘C. Calculate the length of the air column on the cooler side. neglect the changes in the volume of mercury and of the glass.
View SolutionA glass tube sealed at both ends is 100cm long, It lies horizontally with the middle 10cm containing mercury. The two ends of the tube contain air at 27∘Cand at a pressure 76cm of mercury. The air column on one side is maintained at 0∘Cand the other side is maintained at 127∘C. Calculate the length of the air column on the cooler side. neglect the changes in the volume of mercury and of the glass.
View SolutionWhat will be the length of mercury column in a barometer tube, when the atmospheric pressure is 76 cm of mercury and the tube is inclined at an angle of 30∘ with the horizontal direction ?
View Solution
