A thin uniform bar of mass $m$ and length $2 L$ is held at angle $30^{\circ}$ with the horizontal by means of two vertical inextensible strings, at each and as shown in figure. If the string at the right end breaks, leaving the bar to swing the tension in the string at the left end of the bar immediately after string breaks is $T = \frac{n}{13} m g$

Video Solution

Text Solution

Verified by Experts

Just after cutting the string the tension of right will disapear and tension in left string will change. Let us draw free body diagram of rod immediately after the string breaks.

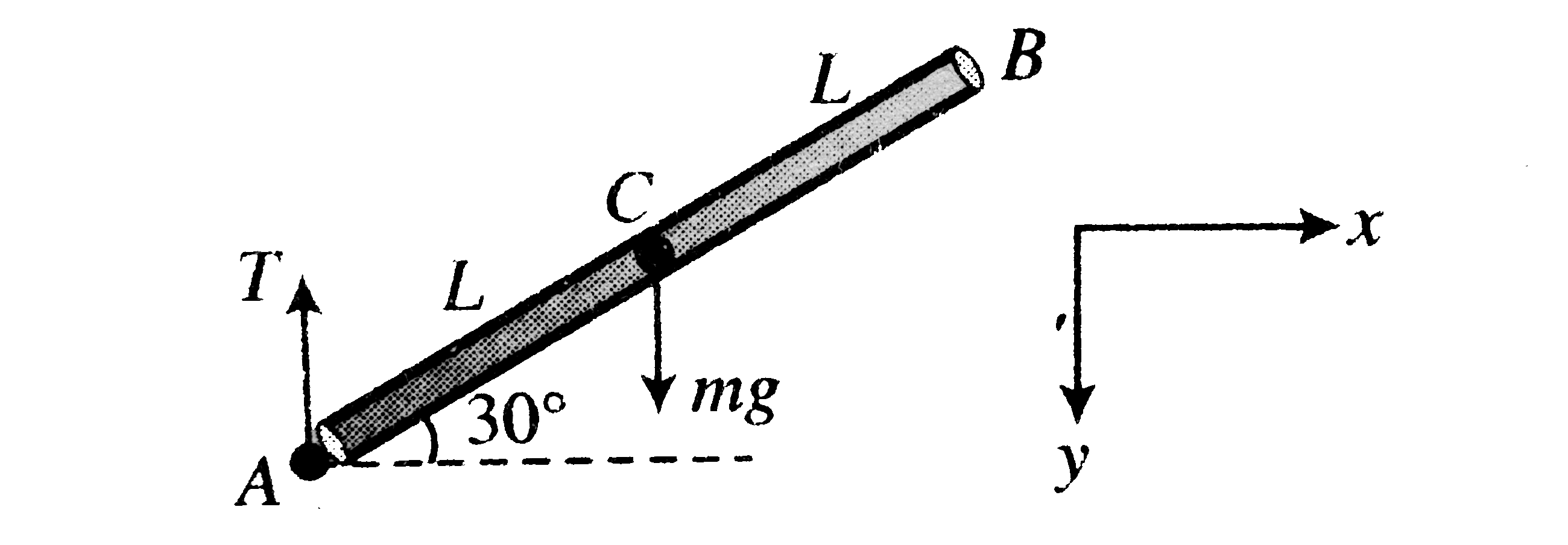
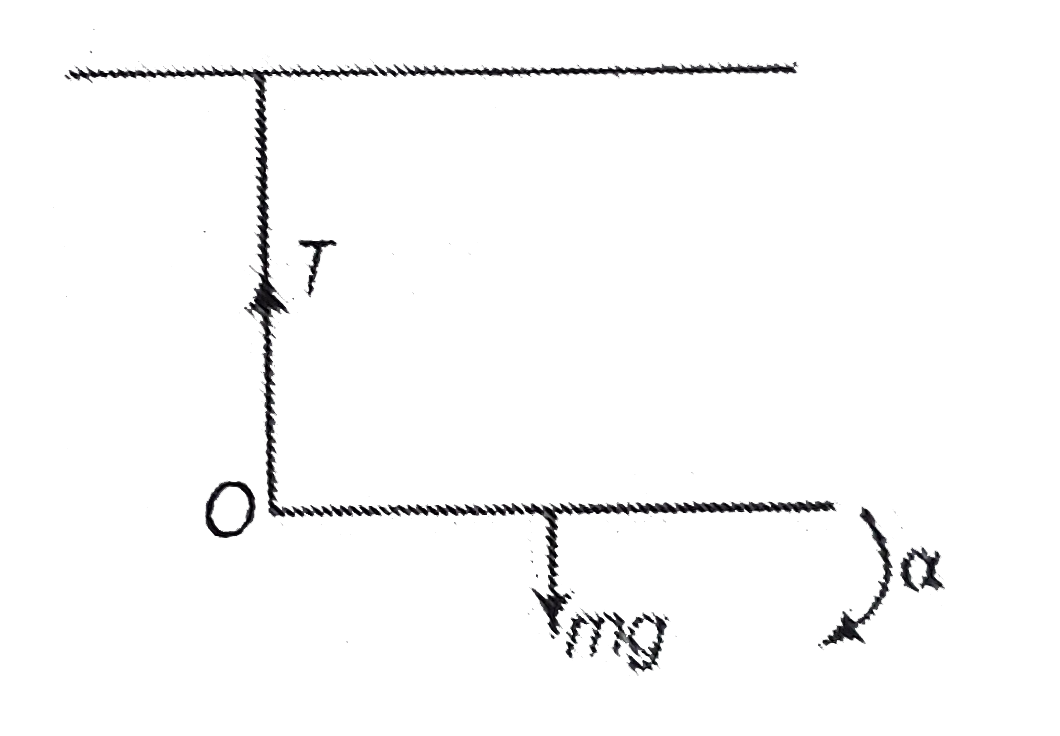
$Σ F_{x} = 0$
$∴ a_{x} = 0$ …….i
$a_{y} = \frac{Σ F_{y}}{m} = \frac{m g - T}{m}$ ........ii

Applying torque equation about centre of mass
$τ = I_{c m} α$
$T . (L {cos 30}^{\circ}) = \frac{3 {(2 L)}^{2}}{12} . α$
$\Rightarrow α = \frac{τ}{I} i = \frac{T L {cos 30}^{\circ}}{\frac{m {(2 L)}^{2}}{12}} = \frac{3 \sqrt{3} T}{2 m L}$ ..........iii

Now just after the string breaks, acceleration of point $A$ in the vertical direction should be zero.
$i . e . a_{y} = L α {cos 30}^{\circ}$ .........iv
Solving equatioin i, ii, iii and iv we get
$T = \frac{2 m g}{11}$ and $a = \frac{3 \sqrt{3}}{11} \frac{g}{L}$

A uniform rod of mass m and length l is suspended by means of two light inextensible strings as shown in figure. Tension in one string immediately after the other string is cut is
A $\frac{m g}{2}$
B2mg
C $\frac{m g}{4}$
Dmg
A rod PQ of mass M and length L is hinged at end P. The rod is kept horizontal by a massless string tied to point Q as shown in figure. When string is cut, the intial angular acceleration of the rod is

A $\frac{3 g}{2 L}$
B $\frac{g}{L}$
C $\frac{2 g}{L}$
D $\frac{2 g}{3 L}$
A uniform rod of length $l$ and mass $M$ is suspended on two vertical inextensible string as shown in figure. Then tension $T$ in the left string at the instant, when right string snaps is?

A $T = M g$
B $T = \frac{M g}{2}$
C $T = \frac{M g}{4}$
D $T =$ zero