Consider two heavy right circular rollers of the radii R and r respectively and rest on a rough horizontal plane a shown in figure. The larger roller has a string wound around it to which a horizontal force P can be applied as shown. Assuming that the coefficient of friction m has the same value for all surfaces of contact, determine the necessary condition under which the larger roller can be pulled over the smaller one. Assume the smaller cylinder should neither roll nor slide.

Figure shows the forces acting on the smaller cylinder. N1 is reaction between the two cylinders and N2 the normal reaction between the smaller cylinder and the horizontal surface.

The conditions of equlibrium are
∑Fx=N1cosα−μN2=μN1cos(90−α)=0.....i
Taking torque about O2 centre of smaller sphere
∑τ=μN1r−μN2r=0
N1=N2..........ii
On substituting equatiuons ii in i, we obtain
μN1+μN1sinα=N1cosα
μ(1+sinα)=cosα............iii
From figure b. sinα=√R−rR+r,cosα=2√RrR+r
Now equation iii becomes: μ(1+R−rR+r)=2√RrR+r
μ=√rR
Hence the required condition is μ≥√rR
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Exercise 2.16videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Exercise 2.217videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer11videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICSCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE2videos
PROPERTIES OF SOLIDS AND FLUIDS
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger2videos
RIGID BODY DYNAMICS 2
Similar Questions
Knowledge Check
- Question 1 - Select One
A heavy and a light cylindrical rollers of diameter D and d respectively rest on a horizontal plane as shown. The larger roller has a string wound around it to which a horizontal force 'P' can be applied as shown. Assuming 'mu' (coefficient of friction) is same at all surfaces of contact, find the critical value of 'mu' such that larger roller can be just pulled over smaller one.
 Aμ=√DdBμ=2√DdCμ=√dDDμ=2√Dd
Aμ=√DdBμ=2√DdCμ=√dDDμ=2√Dd - Question 2 - Select One
A block of mass 15kg is resting on a rough inclined plane as shown in figure ,The block is tied by a horizontal string which has a tension 50N The coefficient of contact is
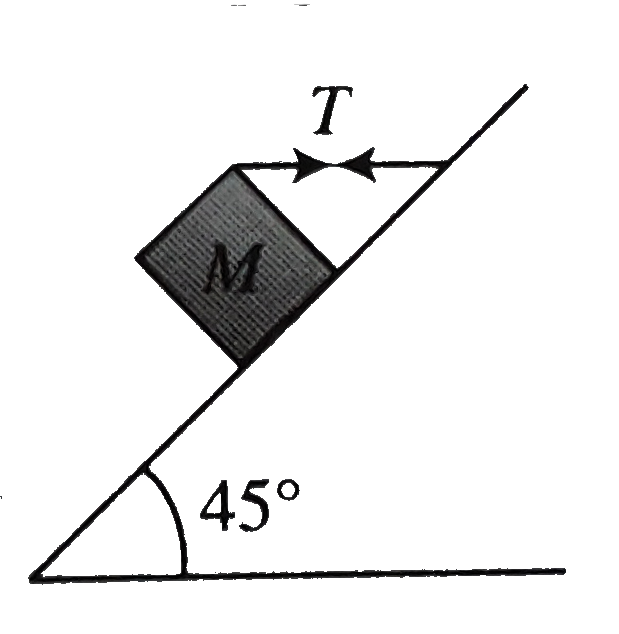 A1/2B2/3C3/4D1/4
A1/2B2/3C3/4D1/4 - Question 3 - Select One
A mass m rests under the action of a force F as shown in the figure-2.158 on a horizontal surface. The coefficient of friction between the mass and the surface is μ. The force of friction between the mass and the surface is :
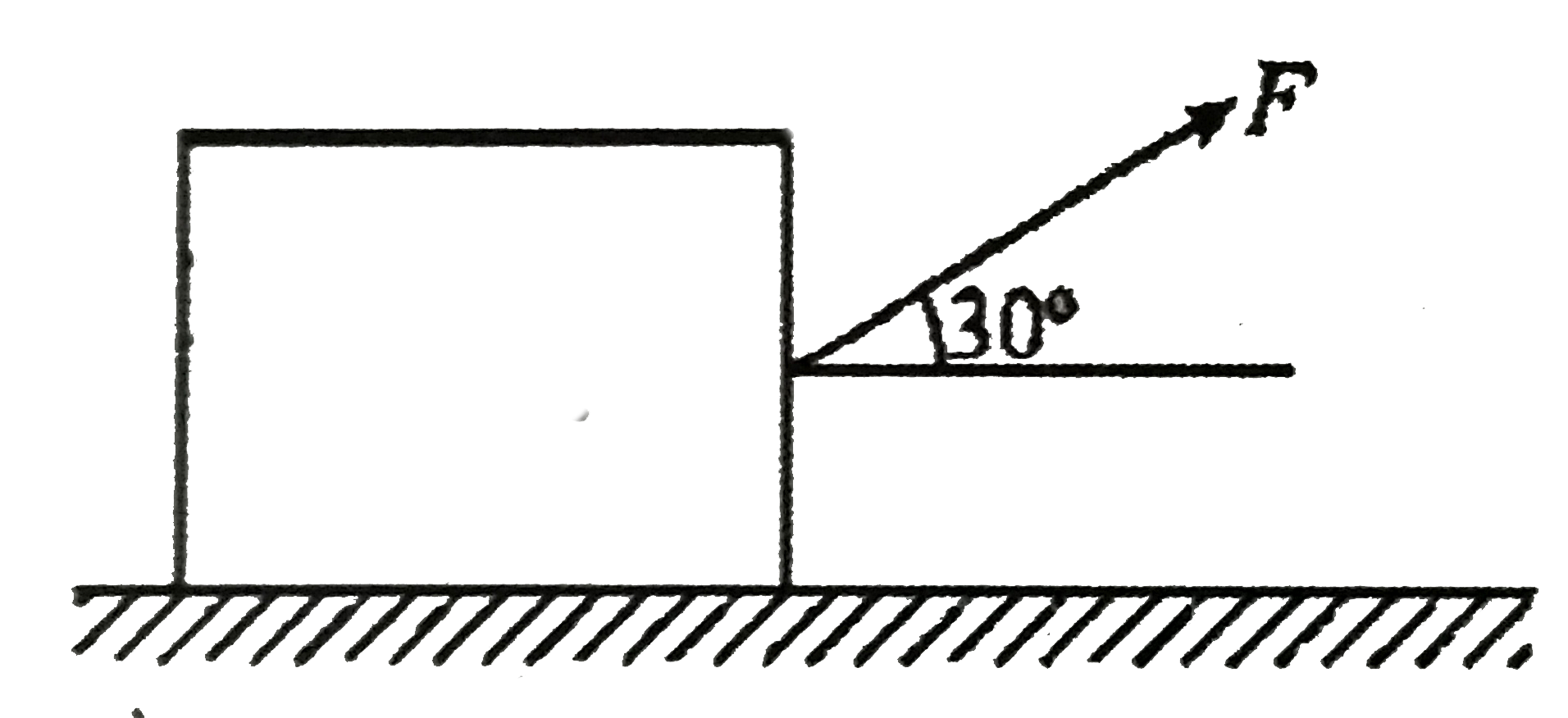 AμmgBμ[mg+F2]CF√32Dμ[mg−F2]
AμmgBμ[mg+F2]CF√32Dμ[mg−F2]
An equilateral prism of mass m rests on a rough horizontal surface with coefficient of friction μ . A horizontal force F is applied on the top of prism as shown in figure. If the coefficient of friction is sufficiently high so that the prism does not slide before topping, the minimum force required to topple the prism is
 View Solution
View SolutionA triangular block mass m rests on a fixed rough inclined plane having friction coefficient μ with the block. A horizontal force F is applied to it as shown in figure below, then the correct statement is :
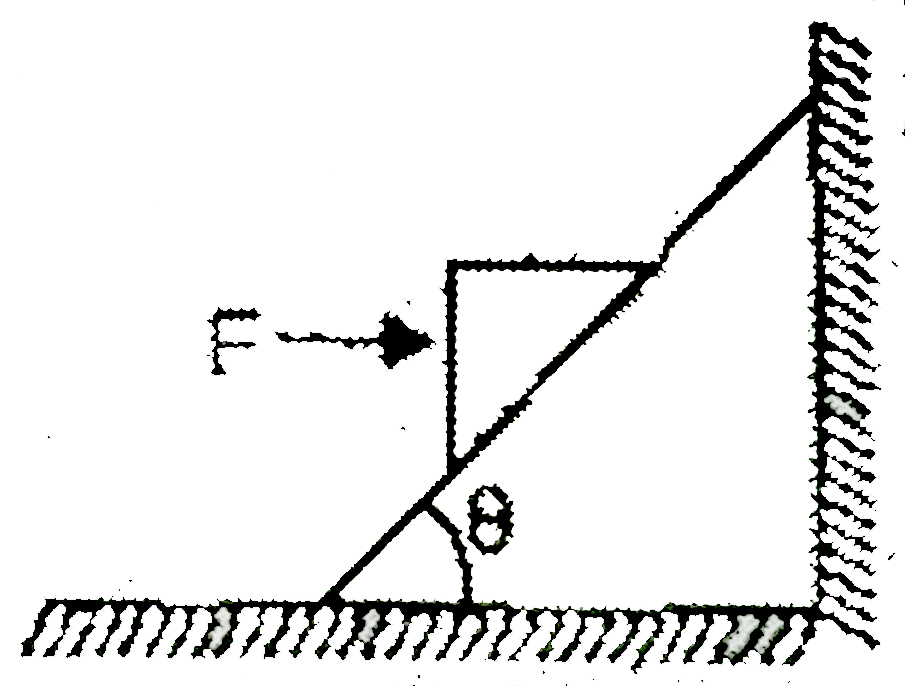 View Solution
View SolutionA triangular block of mass m rests on a fixed rough inclined plane having friction coefficient μ with the block. A horizontal forces F is applied to it as shown in figure below, then the correct statements is:
 View Solution
View SolutionAn equilateral prism of mass m rests on a rough horizontal surface with coefficient of friction μ. A horizontal force F is applied on the prism as shown in the figure. If the coefficient of friction is sufficiently high so that the prism does not slide before toppling, then the minimum force required to topple the prism is -
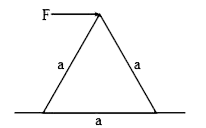 View Solution
View SolutionAn equilateral prism of mass m rests on a rough horizontal surface with cofficent of friction μ. A horizontal force F is applied on the prism as shown in the figure. If the cofficent of the friction is sufficently high so that the prism does not slide before toppling, then the minimum force required to topple the prism is
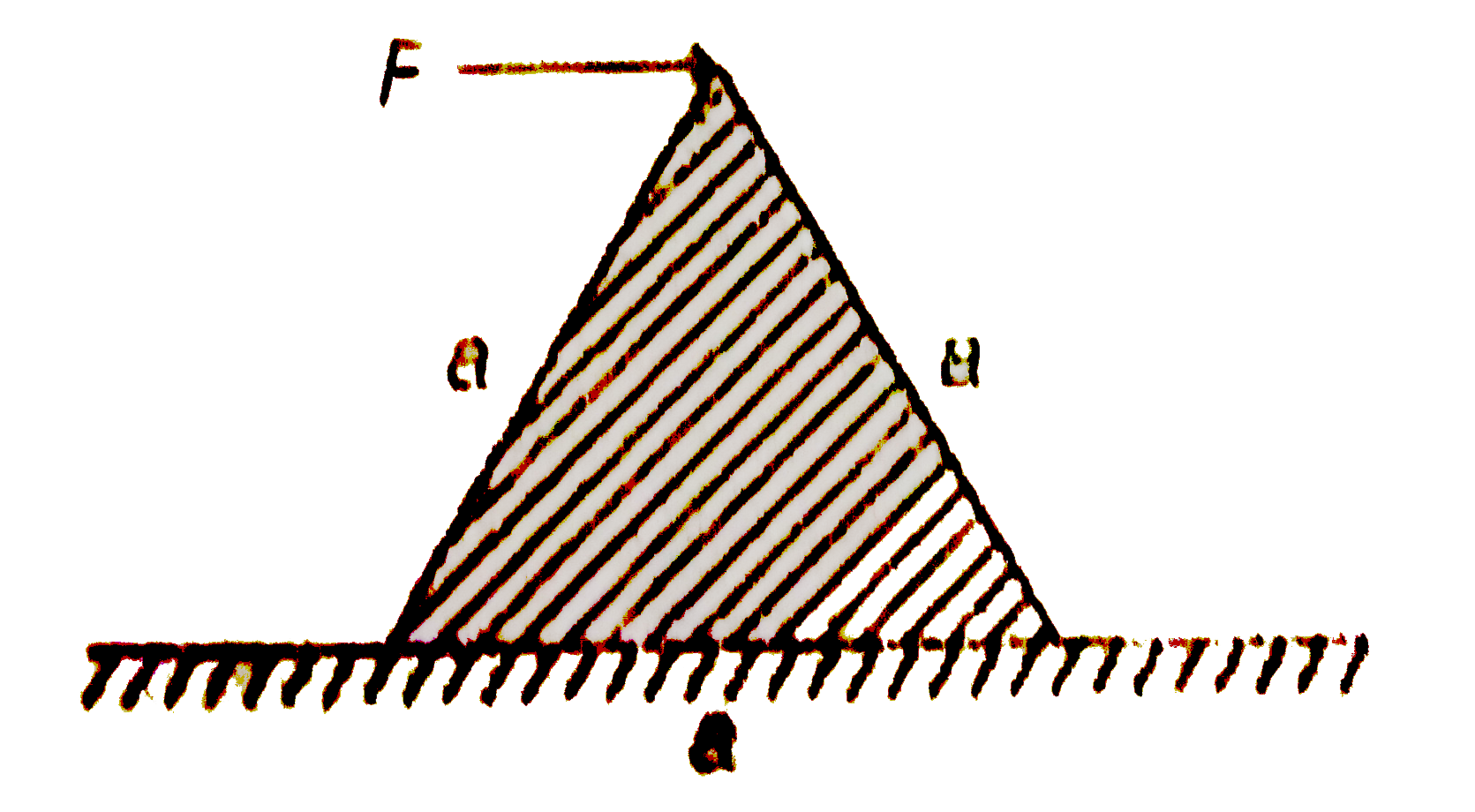 View Solution
View Solution

