A thin uniform rod of length $l$ is initially at rest with respect to an inertial frame of reference. The rod is tapped at one end perpendicular to its length. How far the centre of mass translates while the rod completes one revolution about its centre of mass. Neglect gravitational effect.

Video Solution

Text Solution

Verified by Experts

The impulse delivered perpendicular to the rod at one end gives some linear mometum to the $C M$ (centre of mass) of the rod and also some angular mometum about the $C M$ the rod will rotate about $C M$ free rotation of rigid body always
Translation of $C M$ : Applying impulse momentum equation

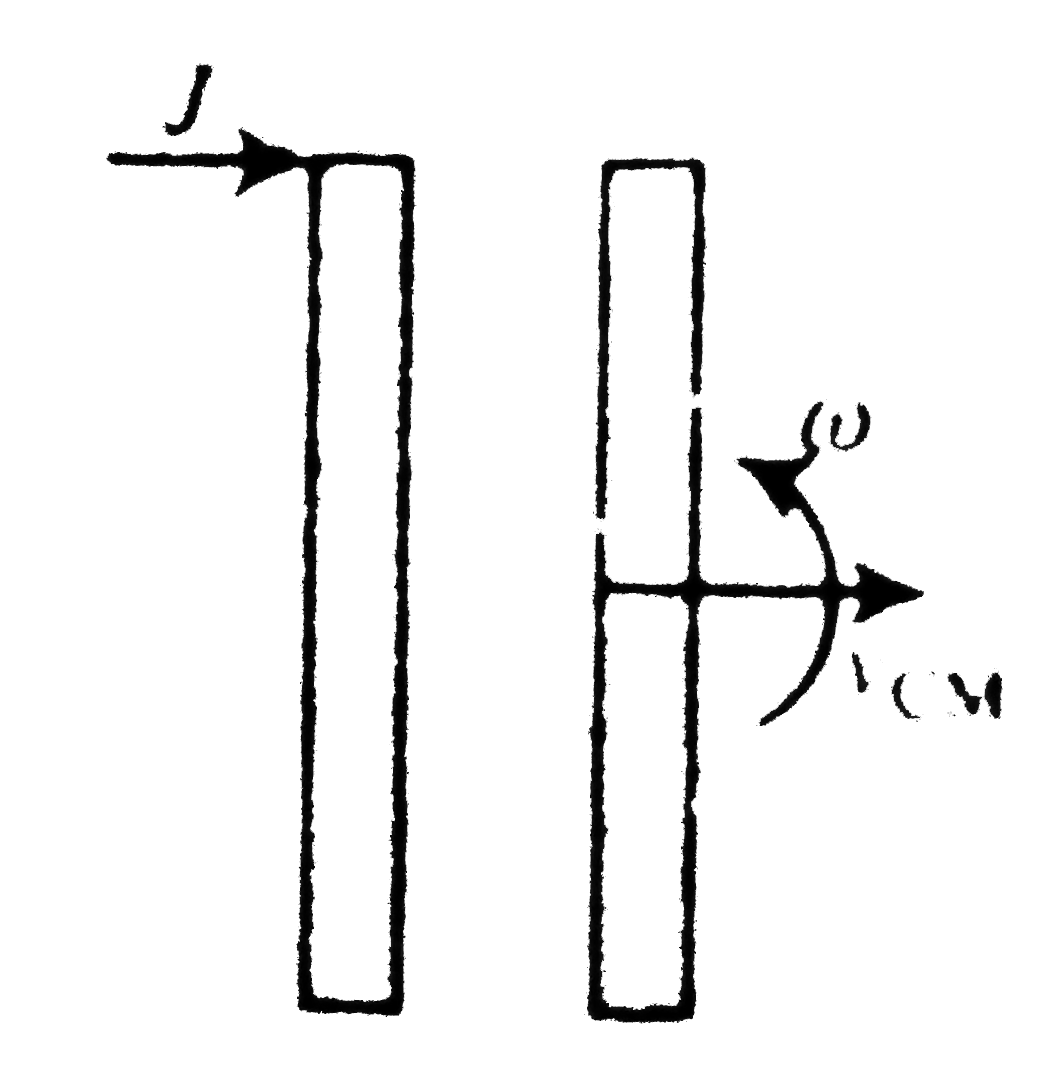
$J = M △ v_{C M}$
$J = M (v_{C M} - 0)$ [initially $C M$ is rest]
Angular impulse about the $C M : J . \frac{L}{2} = I_{C M} △ ω$
Let $△ t$ be the time required for one complete revolution of $2 π$ rad.
Multiplying both side by $△ t$ gives
$M v_{C M} \frac{L}{2} △ t = \frac{M L^{2}}{12} ω △ t$
$\frac{L}{2} (v_{C M} △ t) = \frac{L^{2}}{12} ω △ t [∵ v_{C M} △ t = x]$
$x = \frac{L θ}{6} = x = \frac{L π}{3} [θ = 2 π r a d]$

Updated on:21/07/2023

|

Class 11 PHYSICS RIGID BODY DYNAMICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

The radius of gyration of an uniform rod of length $l$ about an axis passing through one of its ends and perpendicular to its length is.
A $\frac{l}{\sqrt{2}}$
B $\frac{l}{3}$
C $\frac{l}{\sqrt{3}}$
D $\frac{l}{2}$

CENGAGE PHYSICS ENGLISH-RIGID BODY DYNAMICS 2-Exercise 3.4

Home
Ask Doubt
Profile