In the shown figure a mass m slides down the frictionless surface from height h and collides with the uniform vertical rod of length L and mass M after collision the mass m sticks to the rod. The rod is face to rotate in a vertical plane about fixed axis through O. Find the maximum angular deflection of the rod from its initial position.

Just before collision, velocity of the mass m is along the horizontal and is equal to v0=√2gh
In the process of collision only angular momentum of the system will be conserved about the point O.
If L1 and L2 are the angular momentum of the system just before and just after the collision then
L1=mv0L
and L2=Iω=(ML23+mL2)ω
From COAM
(M3+m)L2ω=mv0L
ω=mv0(M3+m)L

Let the rod deflects through an angle theta
Initial energy of rod and mass system =(12)Iω2
where I=(ML22+mL2)
Gain in potential energy of the system
=mgL[1−cosθ]+MgL2[1−cosθ]
=(m+M2)gL(1−cosθ)
∵ From conservation of energy
12Iω2=(m+M2)gL(1−cosθ)
12(ML23+mL2)×m2v20(M3+m)2L2=(m+M2)gL(1−cosθ)
12m2v20[M3+m]=(m=M2)gL(1−cosθ)
cosθ=1−12m2v20[M3+m][M2+m]gL
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Subjective19videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Single Correct142videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Exercise 3.321videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer11videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer16videos
SOUND WAVES AND DOPPLER EFFECT
Similar Questions
A L shaped rod of mass M is free to rotate in a vertical plane about axis A A as shown in figure. Maximum angular acceleration of rod is
 View Solution
View SolutionTwo uniform thin rods each of length L and mass m are joined as shown in the figure. Find the distance of centre of mass the system from point O
 View Solution
View SolutionA uniform rod of length l and mass m is free to rotate in a vertical plane about A as shown in Fig. The rod initially in horizontal position is released. The initial angular acceleration of the rod is
 View Solution
View Solution
A uniform rod of length L is free to rotate in a vertical plane about a fixed horizontal axis through B. The rod begins rotating from rest. The angular velocity ω at angle θ is given asView SolutionA mass m is at a distance a from one end of a uniform rod of length l and mass M. Find the gravitational force on the mass due to the rod.
 View Solution
View SolutionA uniform rod of mass m and length L is free to rotate in the vertical plane about a horizontal axis passing through its end. The rod initially in horizontal position is released. The initial angular acceleration of the rod is:
 View Solution
View SolutionA unifrom rod of length l and mass m is free to rotate in a vertical plane about A, Fig. The rod initially in horizontal position is released. The initial angular acceleration of the rod is (MIof rod aboutAisml23)
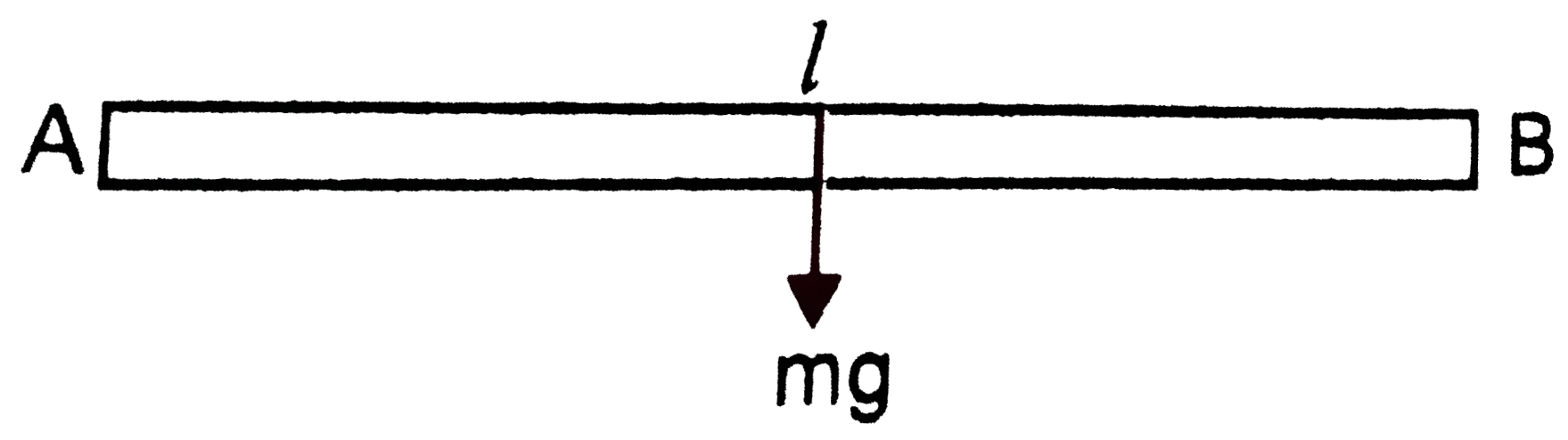 View Solution
View SolutionA mass m is at a distance a from one end of a uniform rod of length l and mass M. Find the gravitational force on the mass due to tke rod.
 View Solution
View SolutionThe moment of inertia of a thing uniform rod of length L and mass M, about axis CD (as shown in figure) is
 View Solution
View SolutionA uniform rod AB of length l and mass m hangs from point A in a car moving with velocity v0 on an inclined plane as shown in Fig. The rod can rotate in vertical plane about the axis at point A. if the car suddenly stops, the angular speed with which the rod starts rotating is
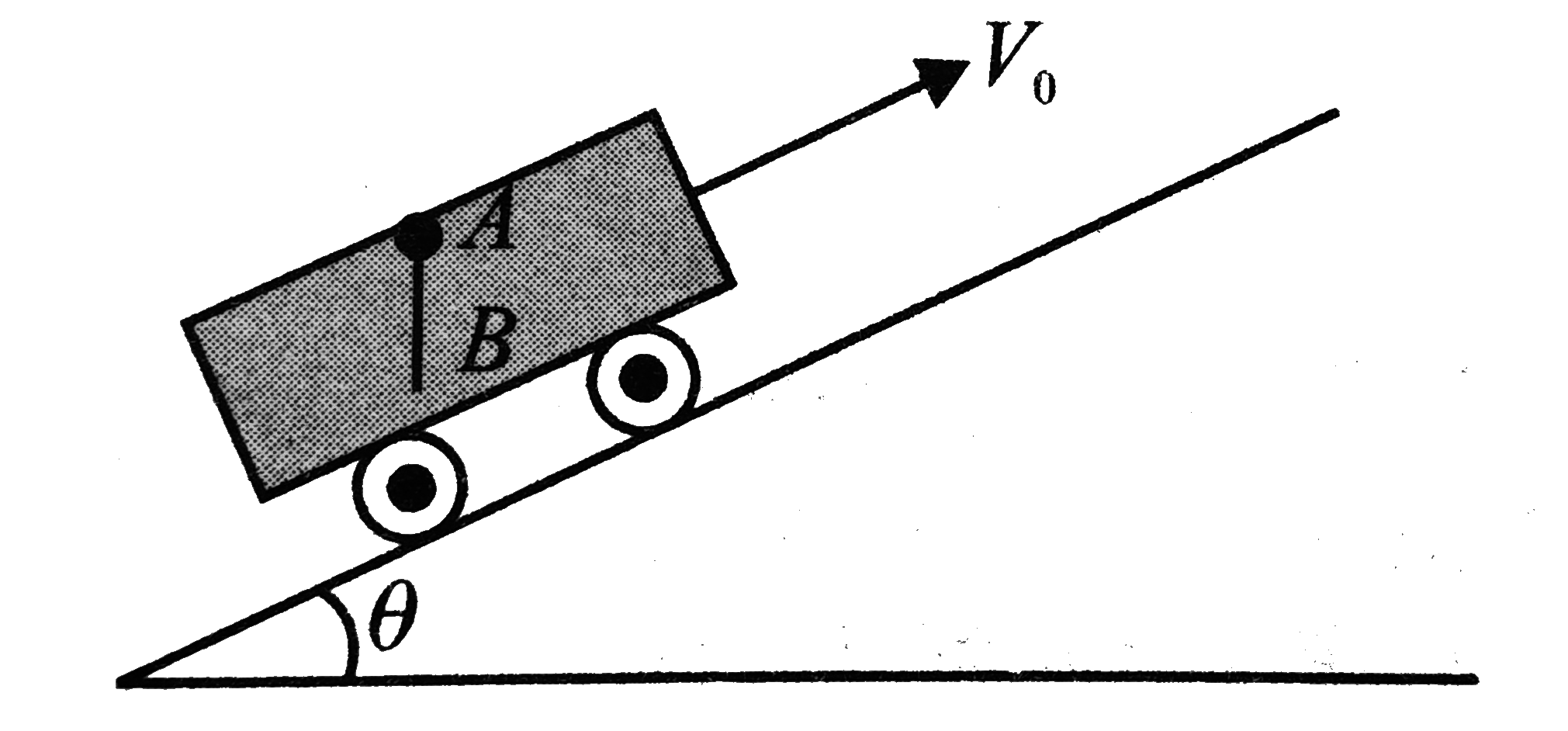 View Solution
View Solution

