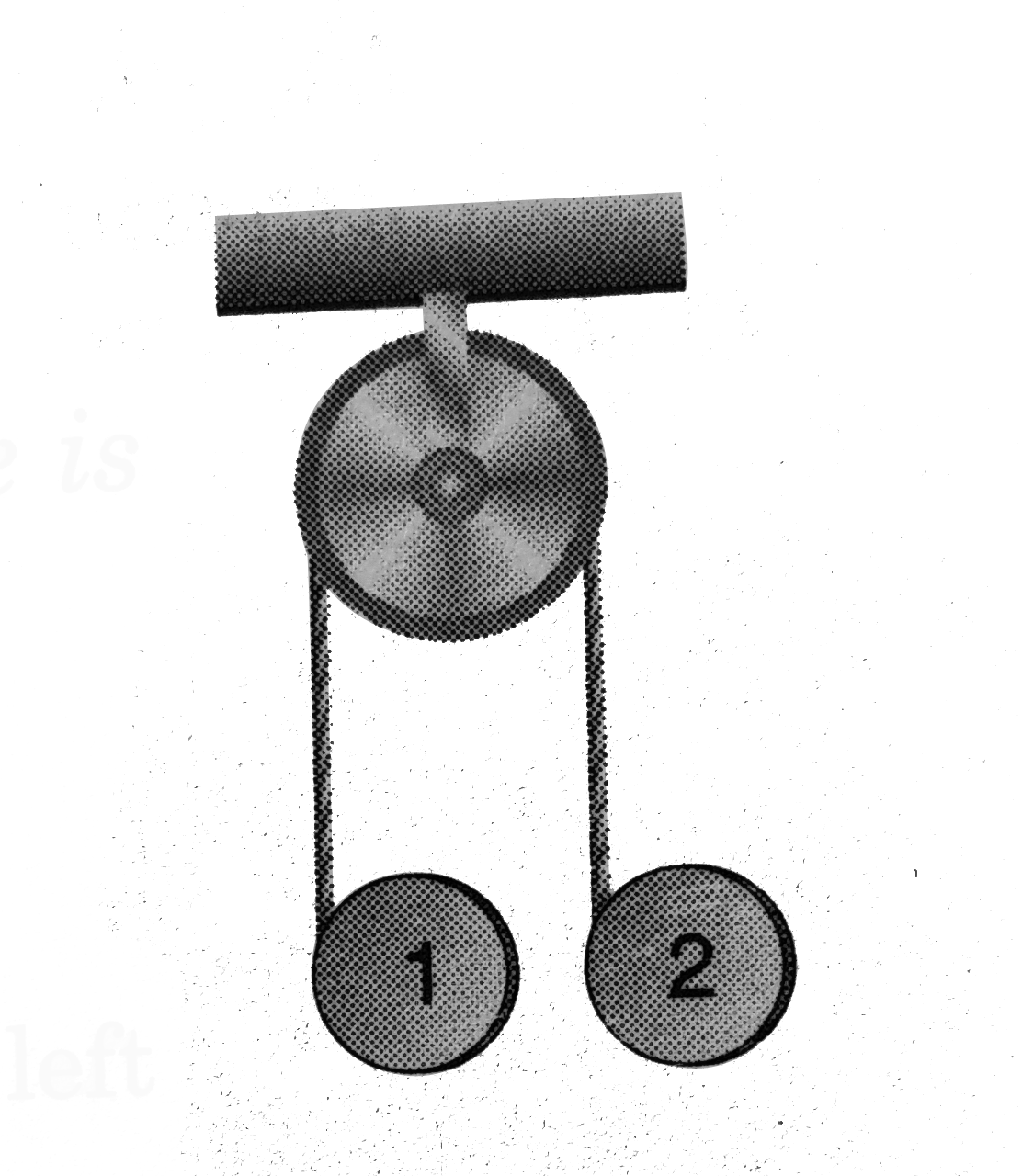
A thread is wound around two discs on either sides. The pulley and the two discs have the same mass and radius. There is no slipping at the pulley and no friction at the hinge. Find out the acceleration of the two discs and the angular acceleration of the pulley.



Let R be the radius of the disc and T1 and T2 be the tensions in the left and right segments of the rope
Acceleration of disc 1,
a1=mg−T1m ..(i)
Acceleration of disc 2, a2=mg−T2m ..(ii)
Angular acceleration of disc 1, α1=τI=T1R12mR2=2T1mR ..(iii)
Similarly, angular acceleration of disc 2, α2=2T2mR ..(iv)
Both α1 and α2 are clockwise.
Angular acceleration of pulley
α=(T2−T1)R12mR2=2(T2−T1)mR ..(v)
For no slipping Ra1=a2−Rα2=Rα ..(vi)
Solving these equation we get
a=0 and a1=a2=2g3
Alternate solution
As both the discs are in identical situation T1=T2 and α=0 i.e, each of the discs falls independently and identically. therefore this is exactly similar to the problem shown in figure.
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Solved Example
1 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Exercise 12.1
10 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Solved Examples
25 Videos
- ROTATIONBOOK - DC PANDEYCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEYCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions
17 Videos
Similar Questions
Consider the situation shown in figure. All the surfaces are frictions and the string and the pulley are light. Find the magnitude of the acceleration of the two blocks.

View SolutionA uniform disc of mass M and radius R is hinged at its centre C . A force F is applied on the disc as shown . At this instant , angular acceleration of the disc is
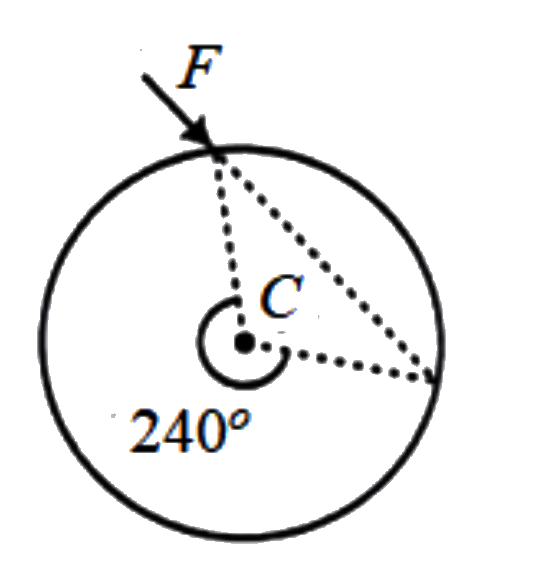
View Solution
Knowledge Check
A uniform disc of mass M and radius R is hinged at its centre C. A force F is applied on the disc as shown. At this instant, the angular acceleration of the disc is
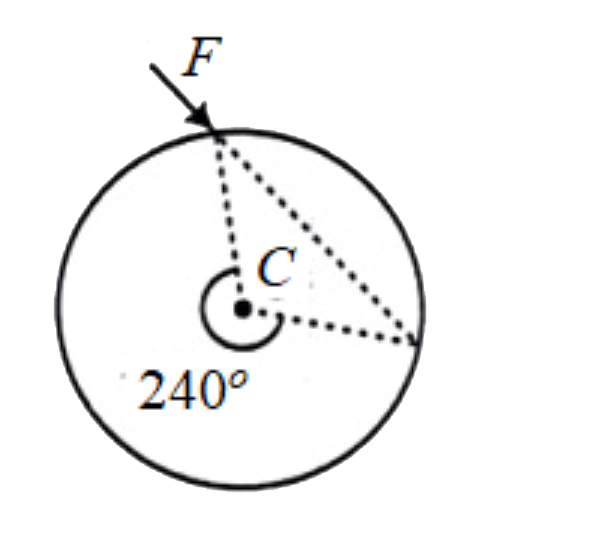 A√3FMRBFMRC2√3FMRDF2MR
A√3FMRBFMRC2√3FMRDF2MRIn the figure shown neglecting friction and mass of pulley, what is the acceleration of mass B ?
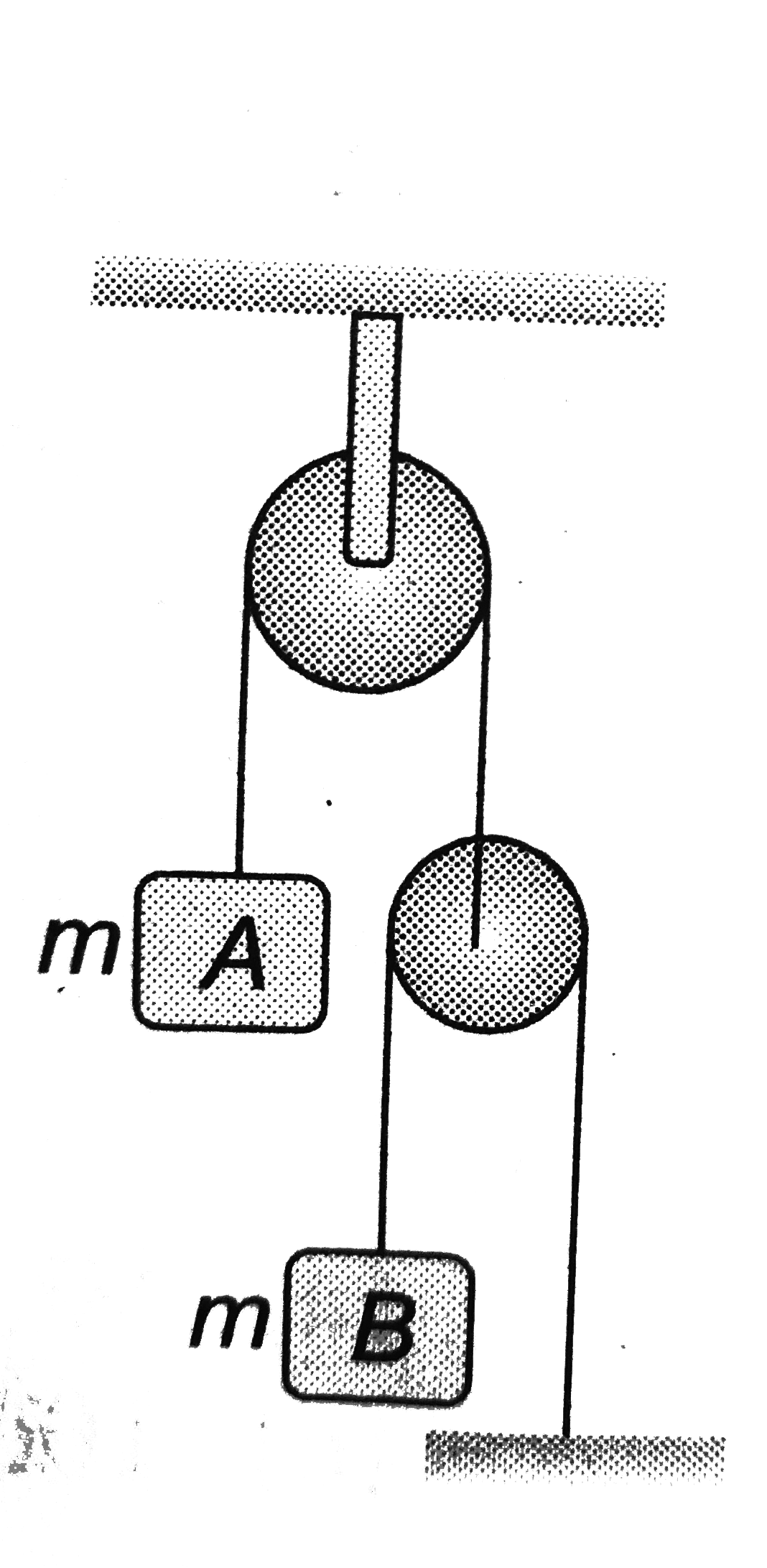 Ag3B5g2C2g2D2g5
Ag3B5g2C2g2D2g5
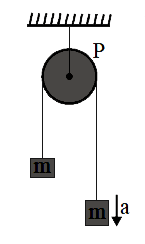
In the figure, the blocks unequal masses m1 and m2 (m1<m2).m2 has a downward acceleration a. The pulley P has a radius r, and some mass. The string does not slip on the pulley. Find the acceleration of block and angular acceleration of pulley. (I = momentum of inerita of pulley)
View SolutionA belt moves over two pulleys A and B as shown in the figure. The pulleys are mounted on two fixed horizontal axles. Radii of the pulleys A and B are 50 cm and 80 cm respectively. Pulley A is driven at constant angular acceleration of 0.8 rad/s2 unitl pulley B acquries an angular velocity of 10 rad/s. The belt does not slide on either of the pulleys.
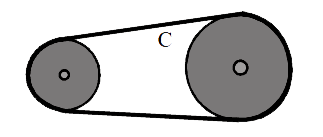
(a)Find the acceleration of a point C on the belt and angular acceleration of the pulley B.
(b) How long does it take for the pulley B to acquire an angular velocity of 10 rad/s ?
View SolutionTwo equal and opposite forces are allplied tangentially to a uniform disc of mass M and radius R as shown in the figure. If the disc is pivoted at its centre and free to rotate in its plane, the angular acceleration of the disc is :

View SolutionWhen we ignore friction and mass of pulley what would be the accelerations of the two blocks m1 and m2
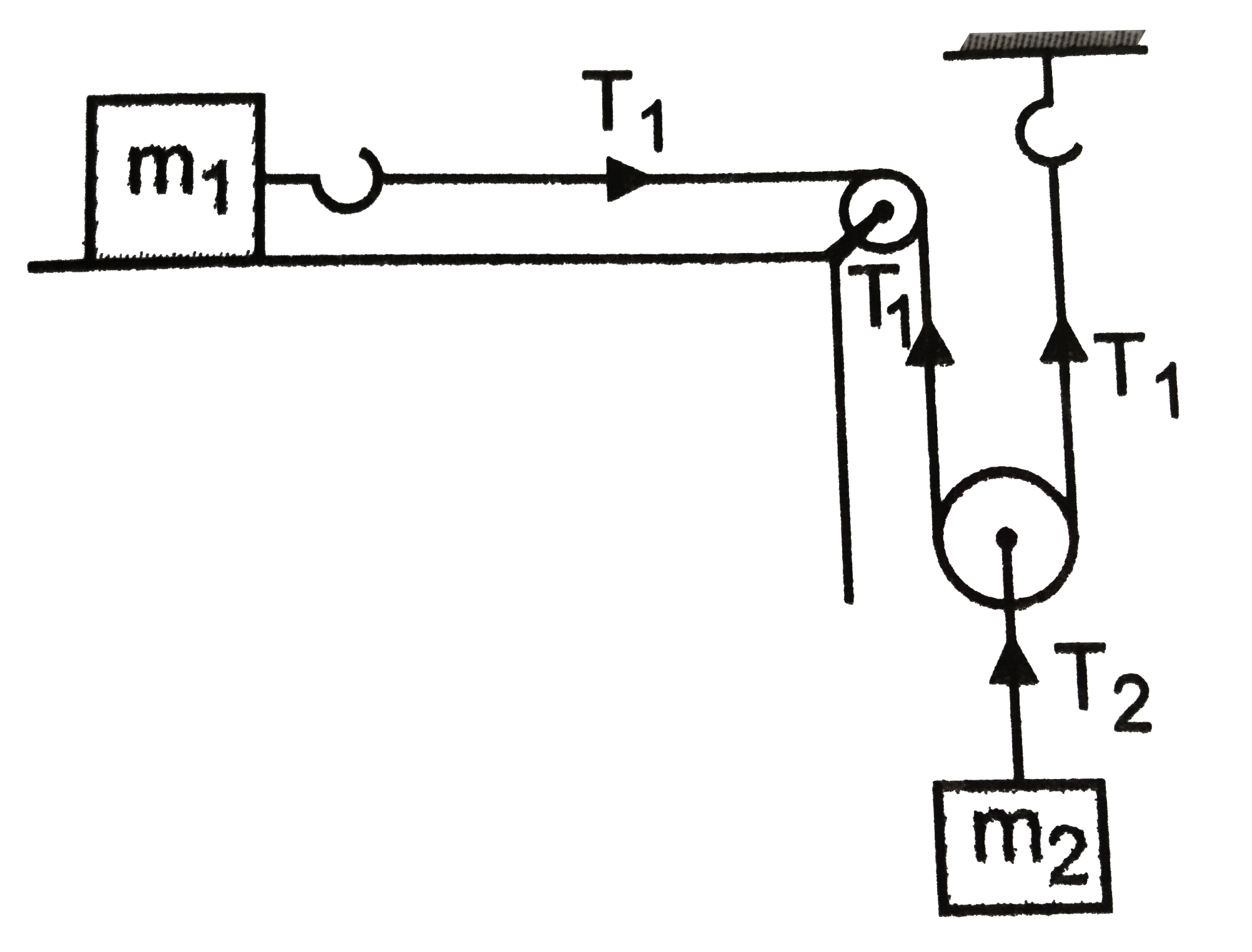 .
.
View Solution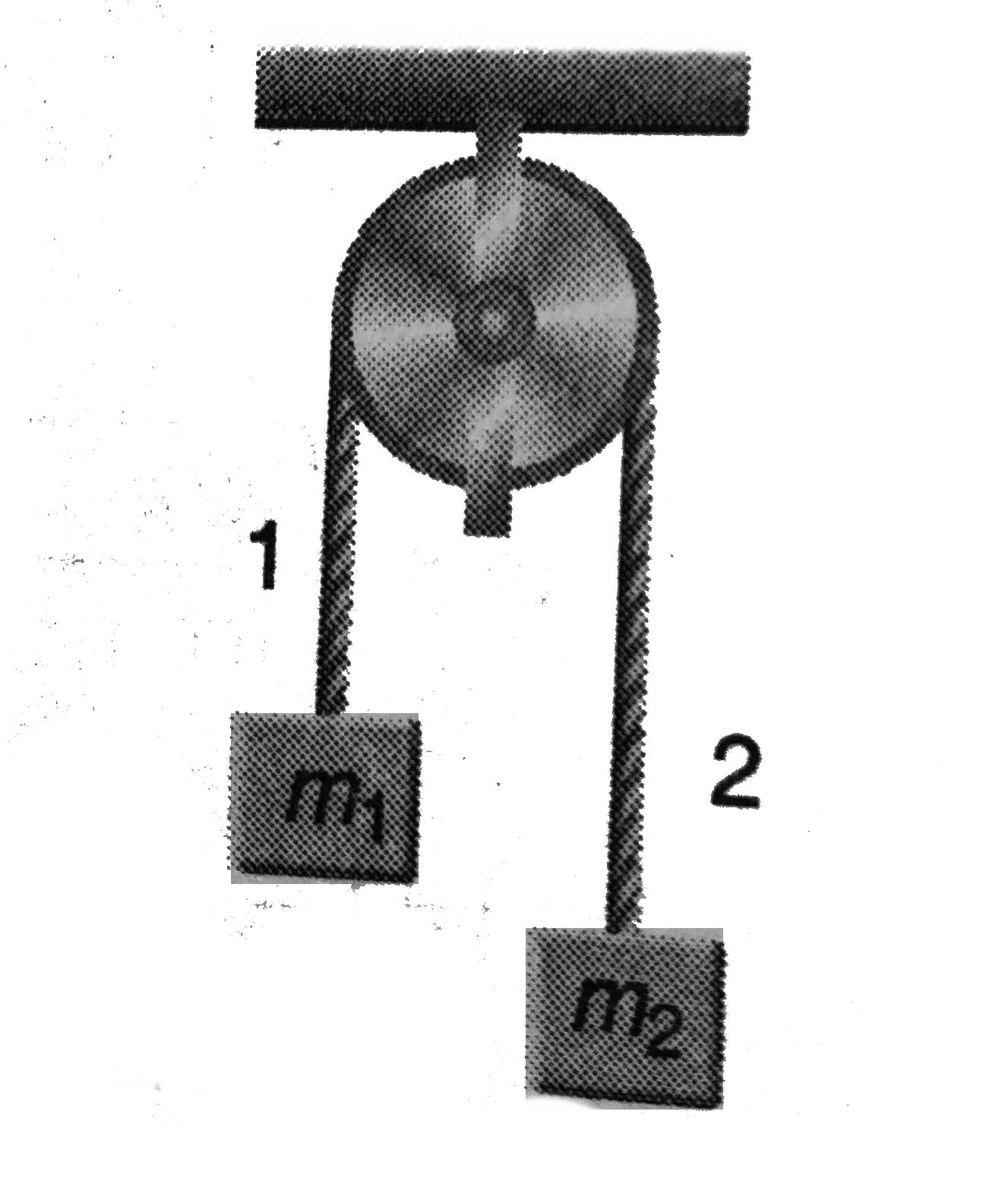
In the arrangement shown in figure the mass of the uniform solid cylindrical pulley of radius R is equal to m and the masses of two bodies are equal to m1 and m2. The thread slipping and the friction in the axle of the pulley are supposed to be absent. Find the angular acceleration of the cylinder and the ratio of tensions T1T2 of the vertical sections of the thread in the process of motion.
View SolutionA disc shaped pulley of mass 'm'=4kg and radius R=0.5m can rotate freely about its center. A block of mass M=2kg hangs from the pulley through is massless string that is tightly wrapped around the pulley. When the system is released, there is no slipping between pulley and string.
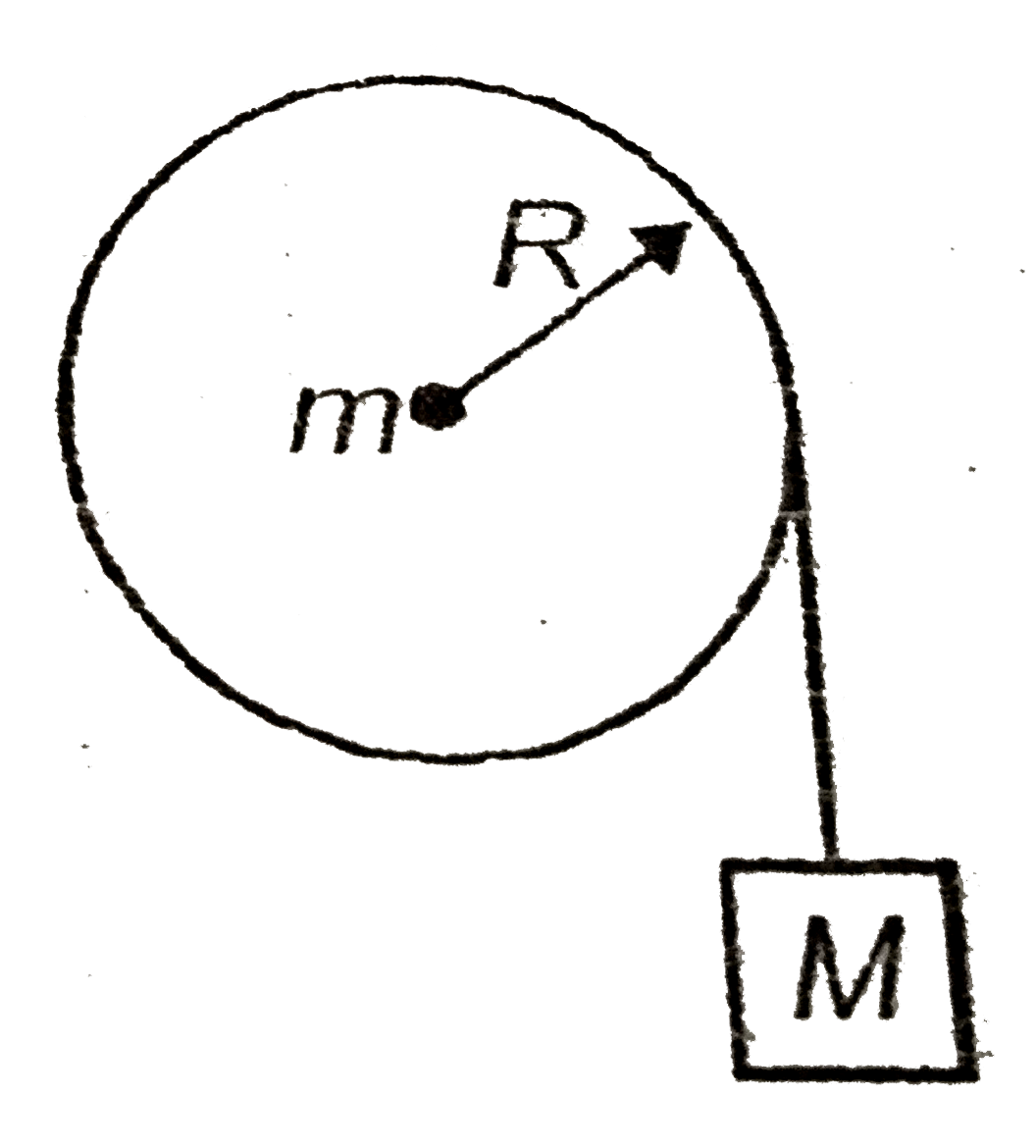
(a) Calculate the angular accelerating of the pulley
(b) Calculate the tension in the string
View Solution
