A toroidal inductor with an inductance of 90 mH encloses a volume of 0.0200 m3. If the average energy density in the toroid is 70.0 J/m3, what is the current through the inductor?
To solve the problem of finding the current through a toroidal inductor given its inductance, volume, and average energy density, we can follow these steps:
1. Identify Given Values:
- Inductance, L=90mH=90×10−3H
- Volume, V=0.0200m3
- Average energy density, uB=70.0J/m3
2. Calculate Total Energy Stored in the Inductor:
The total energy stored in the inductor can be calculated using the formula:
E=uB×V
Substituting the values:
E=70.0J/m3×0.0200m3=1.4J
3. Use the Energy Stored Formula for Inductors:
The total energy stored in an inductor is also given by:
E=12LI2
Setting the two expressions for energy equal to each other:
1.4J=12(90×10−3H)I2
4. Rearranging to Solve for Current I:
Multiply both sides by 2:
2.8=90×10−3I2
Now, divide both sides by 90×10−3:
I2=2.890×10−3=2.80.09≈31.11
5. Taking the Square Root:
I=√31.11≈5.57A
Final Answer:
The current through the inductor is approximately I≈5.57A.
---
- Inductance, L=90mH=90×10−3H
- Volume, V=0.0200m3
- Average energy density, uB=70.0J/m3
The total energy stored in the inductor can be calculated using the formula:
E=uB×V
Substituting the values:
E=70.0J/m3×0.0200m3=1.4J
The total energy stored in an inductor is also given by:
E=12LI2
Setting the two expressions for energy equal to each other:
1.4J=12(90×10−3H)I2
Multiply both sides by 2:
2.8=90×10−3I2
Now, divide both sides by 90×10−3:
I2=2.890×10−3=2.80.09≈31.11
I=√31.11≈5.57A
The current through the inductor is approximately I≈5.57A.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - PRACTICE QUESTIONS (Single Correct Choice Type)
45 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - PRACTICE QUESTIONS (More than One Correct Choice Type)
13 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - CHECKPOINTS
9 Videos
- ELECTRIC POTENTIALBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC POTENTIALEXERCISE - (PRACTICE QUESTIONS) Integer Type
1 Videos
- ELECTROMAGNETIC OSCILLATIONS AND ALTERNATING CURRENT BOOK - RESNICK AND HALLIDAYCHAPTER - ELECTROMAGNETIC OSCILLATIONS AND ALTERNATING CURRENT EXERCISE - Practice Questions (Integer)
7 Videos
Similar Questions
In Fig. 30-44, after switch S is closed at time t = 0, the emf of the source is automatically adjusted to maintain a constant current i through S. (a) Find the current through the inductor as a function of time. (b) At what time is the current through the resistor equal to the current through the inductor?

View SolutionCalculate the energy stored in an inductor of inductance 50 mH when a current of 2.0 A is passed through it.
View Solution
Knowledge Check
A current of 1 A through a coil of inductance of 200 mH is increasing at a rate of 0.5As−1. The energy stored in the inductor per second is
A0.5Js−1B5.0Js−1C0.1Js−1D2.0Js−1A 120 volt AC source is connected across a pure inductor of inductance 0.70 henry. If the frequency of the source is 60Hz, the current passing through the inductor is
A4.55ampsB0.355ampsC0.455ampsD3.55ampsTwo capacitors of capacitance C and 3C are charged to potential difference V0 and 2V0, respectively, and connected to an inductor of inductance L as shows in Fig. Initially, the current in the inductor is zero. Now, switch S is closed.
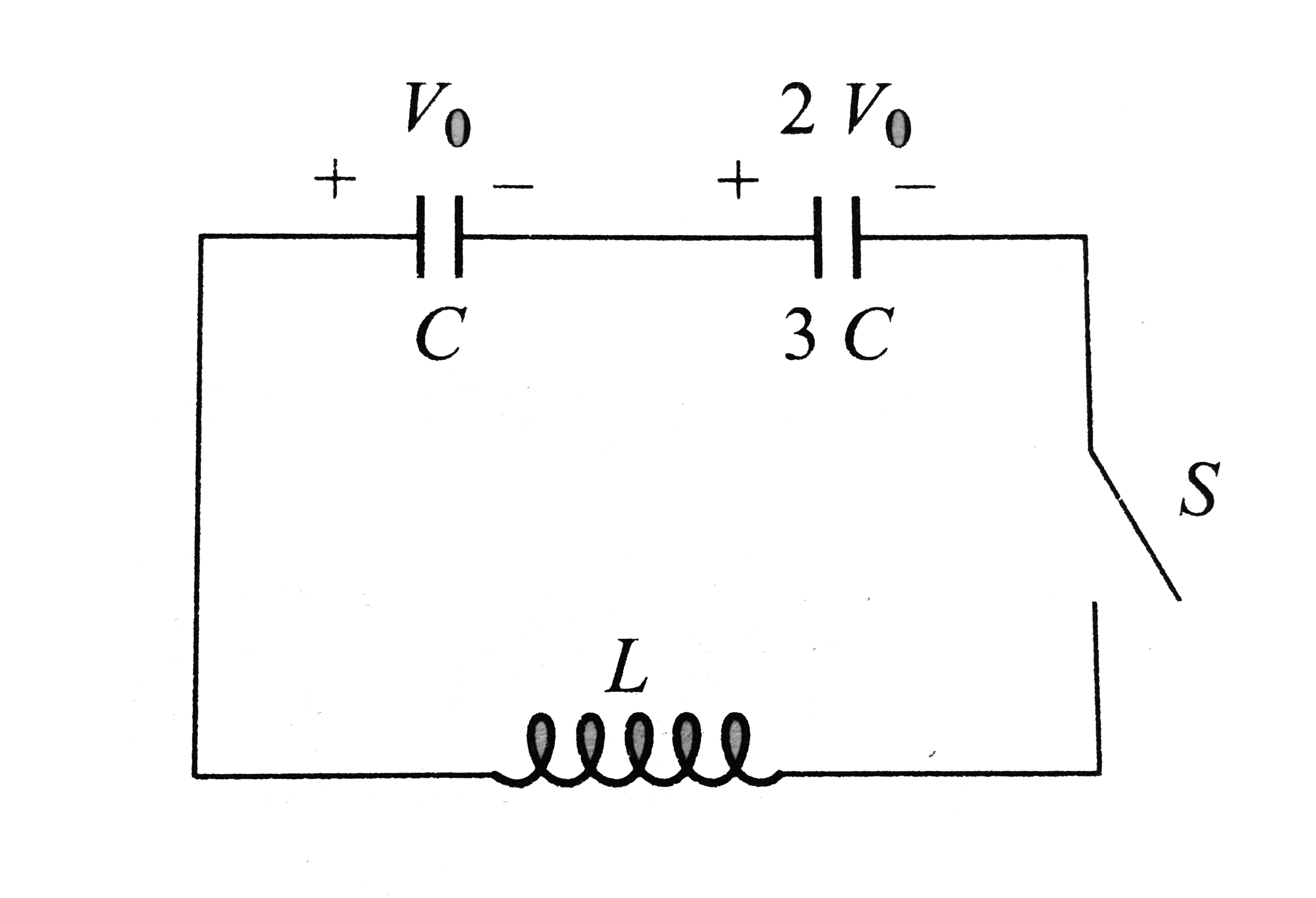
The maximum current in the inductor isA3V02√3CLBV0√3CLC2V0√3CLDV0√CL
At the instant when the current in an inductor magnitude of the self-induced emf is 0.0640A/s, the magnitude fo the self- induced emf is 0.0160V.
(a) What is the inductance of the inductor?
(b) If the inductor is a solenoid with 400 turns, what is the average magnetic flux through each turn when the current is 0.720A?
View SolutionA pure inductor of 25.0 mH is connected to a source of 220 V. Find the inductive reactance and rms current in the circuit if the frequency of the source is 50 Hz.
View SolutionAn L−C circuit consists of an inductor with L=0.0900H and a capacitor of C=4×10−4F. The initial charge on the capacitor is 5.00μC, and the initial current in the inductor is zero.
(a) What is the maximum voltage across the capacitor?
(b) What is the maximum current in the inductor?
(c) What is the maximum energy stored in the inductor?
(d) When the current in the inductor has half its maximum value, what is the charge on the capacitor and what is the energy stored in the inductor?
View SolutionConsider an ideal inductor (having no resistance) of inductance L which is connected to an ideal cell (no resistance) of emf E by closing the switch S at time t=0. Plot the variation of current through the inductor versus time.
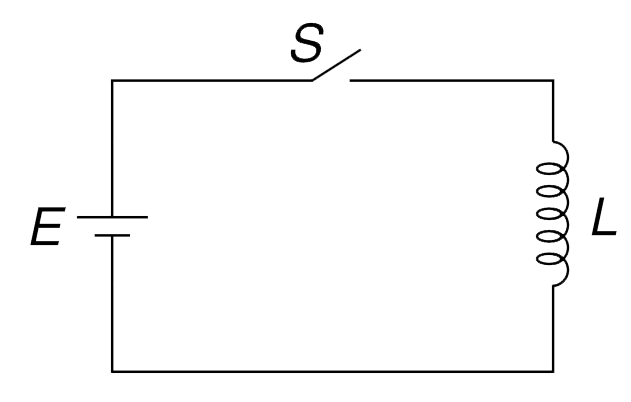
View SolutionIn an oscillating LC circuit, when 75.0% of the total energy is stored in the inductor's magnetic field, (a) what multiple of the maximum charge is on the capacitor and (b) what multiple of the maximum current is in the inductor?
View Solution
