What must be the magnitude of a uniform electric field if it is to have the same energy density as that possessed by a 20 mT magnetic field?
To find the magnitude of a uniform electric field (E) that has the same energy density as a 20 mT magnetic field (B), we can follow these steps:
Step 1: Understand the energy density of electric and magnetic fields
The energy density (u) of an electric field is given by the formula:
uE=12ϵ0E2
where:
- ϵ0 is the permittivity of free space (≈8.85×10−12F/m)
- E is the magnitude of the electric field.
The energy density of a magnetic field is given by:
uB=12B2μ0
where:
- μ0 is the permeability of free space (≈4π×10−7T m/A)
- B is the magnitude of the magnetic field.
Step 2: Set the energy densities equal
Since we want the energy density of the electric field to equal the energy density of the magnetic field, we set:
12ϵ0E2=12B2μ0
Step 3: Simplify the equation
We can cancel out the 12 from both sides:
ϵ0E2=B2μ0
Step 4: Rearrange the equation to solve for E
Rearranging gives us:
E2=B2ϵ0μ0
Taking the square root of both sides:
E=√B2ϵ0μ0
Step 5: Substitute the values
We know that B=20mT=20×10−3T. Now substituting the values of ϵ0 and μ0:
E=
⎷(20×10−3)2(8.85×10−12)(4π×10−7)
Step 6: Calculate the values
1. Calculate (20×10−3)2=400×10−6=4×10−4T2.
2. Calculate ϵ0μ0=(8.85×10−12)(4π×10−7)≈1.112×10−18.
3. Now substitute these into the equation:
E=√4×10−41.112×10−18
Step 7: Final calculation
Calculating this gives:
E≈√3.59×1014≈6×106V/m
Conclusion
Thus, the magnitude of the uniform electric field required to have the same energy density as a 20 mT magnetic field is approximately:
E≈6×106V/m
---
The energy density (u) of an electric field is given by the formula:
uE=12ϵ0E2
where:
- ϵ0 is the permittivity of free space (≈8.85×10−12F/m)
- E is the magnitude of the electric field.
uB=12B2μ0
where:
- μ0 is the permeability of free space (≈4π×10−7T m/A)
- B is the magnitude of the magnetic field.
Since we want the energy density of the electric field to equal the energy density of the magnetic field, we set:
12ϵ0E2=12B2μ0
We can cancel out the 12 from both sides:
ϵ0E2=B2μ0
Rearranging gives us:
E2=B2ϵ0μ0
Taking the square root of both sides:
E=√B2ϵ0μ0
We know that B=20mT=20×10−3T. Now substituting the values of ϵ0 and μ0:
E=
⎷(20×10−3)2(8.85×10−12)(4π×10−7)
1. Calculate (20×10−3)2=400×10−6=4×10−4T2.
2. Calculate ϵ0μ0=(8.85×10−12)(4π×10−7)≈1.112×10−18.
3. Now substitute these into the equation:
E=√4×10−41.112×10−18
Calculating this gives:
E≈√3.59×1014≈6×106V/m
Thus, the magnitude of the uniform electric field required to have the same energy density as a 20 mT magnetic field is approximately:
E≈6×106V/m
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBook:RESNICK AND HALLIDAYChapter:ELECTROMAGNETIC INDUCTIONExercise:PRACTICE QUESTIONS (Single Correct Choice Type)
Explore 45 Videos
- ELECTROMAGNETIC INDUCTIONBook:RESNICK AND HALLIDAYChapter:ELECTROMAGNETIC INDUCTIONExercise:PRACTICE QUESTIONS (More than One Correct Choice Type)
Explore 13 Videos
- ELECTROMAGNETIC INDUCTIONBook:RESNICK AND HALLIDAYChapter:ELECTROMAGNETIC INDUCTIONExercise:CHECKPOINTS
Explore 9 Videos
- ELECTRIC POTENTIALBook:RESNICK AND HALLIDAYChapter:ELECTRIC POTENTIALExercise:(PRACTICE QUESTIONS) Integer Type
Explore 1 Video
- ELECTROMAGNETIC OSCILLATIONS AND ALTERNATING CURRENT Book:RESNICK AND HALLIDAYChapter:ELECTROMAGNETIC OSCILLATIONS AND ALTERNATING CURRENT Exercise:Practice Questions (Integer)
Explore 7 Videos
Similar Questions
Knowledge Check
Write the expression for energy density of electric field E in free space.
A1/2ε0E2Bε0E2C2ε0E2Dε0E
In an electromagnetic wave, the amplitude of electri field is 1 V/m, What is
(i) the amplitude of magnetic field?
(ii) average energy density of electric field ?
(iii) average energy density of magnetic field ?
(iv) average energy density of wave ?
View SolutionShow that the avearge energy density of the electric field →E equals the average energy density of the magnetic field →B, in electromagnetic waves.
View SolutionA current I, indicated by the crosses in fig. is established in a strip of copper of height h and width w. A uniform field of magnetic induction B is applied at right angles to the strip.
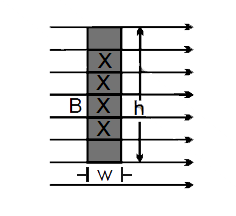
What would the magnitude & direction of homogeneous electric field E have to be in order to counter balance the effect of the magnetic field?
View SolutionIn a plane electomagnetic wave, the electric field oscillates sinusoidally at a frequency of 2.0×106(10)Hz and amplitude 48Vm−1.
(a) What is the wavelength of the wave?
(b) What is the amplitude of the ocillating magnetic field ?
(c ) Show that the average energy density of the →E field equals the average energy density of the →B field.
View SolutionShow that the average energy density of the electric field →E equals the average energy density of the magnetic field →B, in electromagnetic waves.
View SolutionIn an uniform electric field,the potential difference between two points separated by 10cm is 2 volt.Magnitude of electric field .
View SolutionShow that the avearge energy density of the electric field →E equals the average energy density of the magnetic field →B, in electromagnetic waves.
View Solution
