A track consists of two circular pars ABC andCDE of equal rdius 100 m and joined smoothly as shown in figure.Each part sutends a right ngle at its centre. A cycle weighing 100 kg together with rider travels at a constant speed of 18 km/h on the track. A. Findteh nromal contct force by tehroad on the cycle whenit is at B and at D. b.Findteh force of friction exerted by the track on the tyres when the cycle is at B,C and D. c. Find the normal force between teh road and teh cycle just before and just after the cycle crosses C. d. What should be the minimum friction coefficient between the road and the tyre, which will ensure that teh cyclist can move with constant speed? Take g=10ms2

v=18kmh−2=180060×60=5ms−1
a. At point B verious forces acting on the cyclist are
i Weight , mg vertically downwards
ii Normal force , NB by the road upward
Since under the action of these two forces the cyclist moves in a circular path of radius r from the dynarrics of circular motion .
mv2r=mg−NB
⇒NB=m(g−v2r)=100(10−52100)=975N
At point D various force acting on the cyclist are
i. Weight , mg vertically downwards
ii Normal force , ND by the road upward
ND−mg=mv2r
⇒ND=mg(g+v2r)=100(10+52100)=1025N
b. At point B and D. the tracks are almost horizontal therefore , there is no component of g along the track at those point that will changs the speed of the cyclist since the cyclist moves with a constant speed , the friction force the at these two points is neccessarily zero.
At point C however of mg along the track that tends to accelerate the motion of the cyclist =mgsinappha
But since his speed remainn constant , a force equal and opposite to mgsinα must be acting on it and this force is the force of friction μNc where μ is the friction coefficient between the road and the type and Nc is the normal reaction at point C
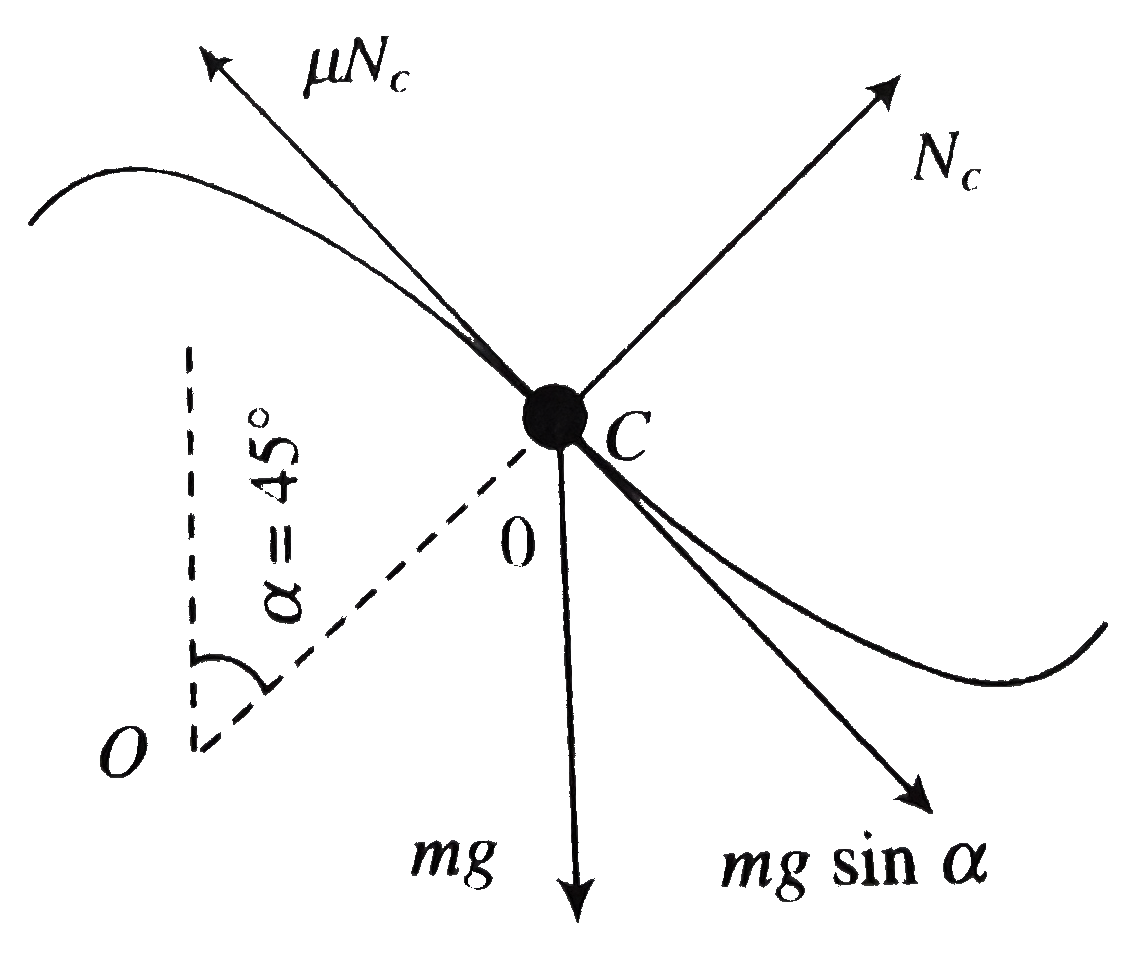
Hence friction force at C is
μNc=mgsinα=100×10×sin45∘=707.12N
c. Just before the cyclist crosses point C varius force acting on him are
i. His weight, mg, vertically downwards, and
ii. Normal force Nb of the track
Hence ,from the dynamics of circular motion,we have
mgcosα−Nb=mv2r
Nb=m(gcosα−v2r)=682.11N
Just after the cyclist crosses the point C varius forces acting on him are
i. Weight, mg, vertically downwards, and
ii. Normal force Nd of the track
Hence ,from the dynamics of circular motion ,
Ndmgcosα=mv2r
⇒Nd=m(gcosα+v2r)=7.32.11N
d. The tendecy of the cyclist to skid is maximum just before the point C , the point is so because the carve is steepest at this point , Force along the track at this point =mgsinα
And friction force =μNb where Na is the normal force of of the track just before the point C
The cyclist can move with constant speed if the two forces are equal and opposite
μNb=mgsinα⇒μ=1.037
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Exercise 7.125videos
NEWTON'S LAWS OF MOTION 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Exercise 7.216videos
NEWTON'S LAWS OF MOTION 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type1videos
NEWTON'S LAWS OF MOTION 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Integer5videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE2videos
PROPERTIES OF SOLIDS AND FLUIDS
Similar Questions
A track consists of two circular pars ABC and CDE of equal radius 100 m and joined smoothly as shown in figure.Each part subtends a right angle at its centre. A cycle weighing 100 kg together with rider travels at a constant speed of 18 km/h on the track. A. Find the normal contact force by the road on the cycle when it is at B and at D. b.Find the force of friction exerted by the track on the tyres when the cycle is at B,C and D. c. Find the normal force between the road and the cycle just before and just after the cycle crosses C. d. What should be the minimum friction coefficient between the road and the tyre, which will ensure that the cyclist can move with constant speed? Take g=10ms2
 View Solution
View SolutionA scooter weighing 150 kg together with its rider moving at 36 km/hr is to take a turn of radius 30 m. What horizontal force on the scooter is needed to make the turn possible?If the horizontal force needed for the turn in the previous problem is to be supplied by the normal force by the road what should be the proper angle of banking?
View Solution
Knowledge Check
- Question 1 - Select One
The mass of a bicycle rider along with the bicycle is 100 kg. he wants to cross over a circular turn of radius 100 m with a speed of 10ms−1. If the coefficient of friction between the tyres and the road is 0.6, will the rider be able to cross the turn? Take g=10ms−2.
A300NB600NC1200ND150N
In the figure shown, the force of friction between A and B will be :
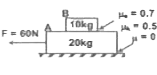 View Solution
View SolutionA scooter weighing 150 g together with its rider moving at 36 km/hr is to take a turn of radius 30 m. What horizontal force on the scooter is needed to make the turn possible?
View SolutionA vehicle is moving on a track with constant speed as shown in figure. The apparent weight of the vehicle is
 View Solution
View SolutionA car runs at constant speed around the horizontal race track shown in the figure. Over which portion of the track is the magnitude of the acceleration the greatest?
 View Solution
View SolutionIn the figure shown, a particle is released from the position A on a smooth track. When the particle reaches at B, then normal reaction on it by the track. When the particle reaches at B, then normal reaction on it by the track is
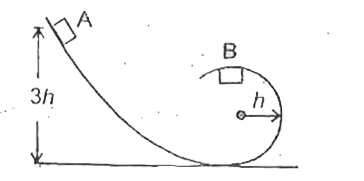 View Solution
View SolutionA particle of mass m moves with constant speed v on a circular path of radius r as shown in figure. The average force on it during its motion from A to B is
 View Solution
View SolutionA force of 100 N is applied on a block of mass 3 kg as shown in figure. The coefficient of friction between the surface and the block is 14 .Then the friction force acting on the block is
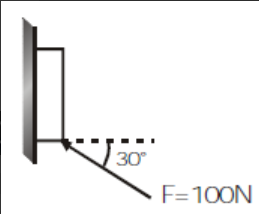 View Solution
View Solution
