A train starts from rest and moves with a constant accelerationof 2.0 for half a minute. The brakes are then applied and the train comes to rest in one minute. Find a. the total distance moved by the train, b. the maximum speed attained by the train and c. the position(s) of the train at half the maximum speed.
To solve the problem step by step, we will break it down into three parts as per the questions asked:
Part A: Total Distance Moved by the Train
1. Calculate the distance during acceleration:
- The train starts from rest, so initial velocity u=0.
- The acceleration a=2m/s2.
- The time of acceleration t=30s.
- We can use the formula for distance covered under constant acceleration:
S1=ut+12at2
- Substituting the values:
S1=0⋅30+12⋅2⋅(30)2=12⋅2⋅900=900m
2. Calculate the distance during deceleration:
- After 30 seconds, the train reaches a speed v which can be calculated using:
v=u+at=0+2⋅30=60m/s
- The train comes to rest in 1 minute (60 seconds), so the time t=60s.
- Using the formula for distance during deceleration:
S2=ut+12at2
- Here, u=60m/s and a=−6060=−1m/s2 (deceleration).
- Substituting the values:
S2=60⋅60+12⋅(−1)⋅(60)2=3600−1800=1800m
3. Total distance moved by the train:
- The total distance S is the sum of S1 and S2:
S=S1+S2=900+1800=2700m
Part B: Maximum Speed Attained by the Train
- The maximum speed attained by the train is v=60m/s (calculated during the acceleration phase).
Part C: Position(s) of the Train at Half the Maximum Speed
1. Calculate half the maximum speed:
- Half of the maximum speed =602=30m/s.
2. Find the position when the speed is 30 m/s during acceleration:
- Using the equation v2=u2+2as:
302=02+2⋅2⋅s
- Solving for s:
900=4s⟹s=9004=225m
3. Find the position when the speed is 30 m/s during deceleration:
- Using the same equation v2=u2+2as:
302=602+2⋅(−1)⋅s
- Solving for s:
900=3600−2s⟹2s=3600−900=2700⟹s=27002=1350m
4. Total positions:
- The positions at half the maximum speed are:
- During acceleration: 225m
- During deceleration: 900+1350=2250m
Final Answers:
- a. Total distance moved by the train: 2700 m
- b. Maximum speed attained by the train: 60 m/s
- c. Positions of the train at half the maximum speed: 225 m and 2250 m
- The train starts from rest, so initial velocity u=0.
- The acceleration a=2m/s2.
- The time of acceleration t=30s.
- We can use the formula for distance covered under constant acceleration:
S1=ut+12at2
- Substituting the values:
S1=0⋅30+12⋅2⋅(30)2=12⋅2⋅900=900m
- After 30 seconds, the train reaches a speed v which can be calculated using:
v=u+at=0+2⋅30=60m/s
- The train comes to rest in 1 minute (60 seconds), so the time t=60s.
- Using the formula for distance during deceleration:
S2=ut+12at2
- Here, u=60m/s and a=−6060=−1m/s2 (deceleration).
- Substituting the values:
S2=60⋅60+12⋅(−1)⋅(60)2=3600−1800=1800m
- The total distance S is the sum of S1 and S2:
S=S1+S2=900+1800=2700m
- Half of the maximum speed =602=30m/s.
- Using the equation v2=u2+2as:
302=02+2⋅2⋅s
- Solving for s:
900=4s⟹s=9004=225m
- Using the same equation v2=u2+2as:
302=602+2⋅(−1)⋅s
- Solving for s:
900=3600−2s⟹2s=3600−900=2700⟹s=27002=1350m
- The positions at half the maximum speed are:
- During acceleration: 225m
- During deceleration: 900+1350=2250m
- a. Total distance moved by the train: 2700 m
- b. Maximum speed attained by the train: 60 m/s
- c. Positions of the train at half the maximum speed: 225 m and 2250 m
Topper's Solved these Questions
- REST AND MOTION : KINEMATICSBOOK - HC VERMACHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Objective 2
10 Videos
- PHYSICS AND MATHEMATICSBOOK - HC VERMACHAPTER - PHYSICS AND MATHEMATICSEXERCISE - Exercises
34 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMACHAPTER - ROTATIONAL MECHANICSEXERCISE - Exercises
86 Videos
Similar Questions
A train starte from rest and moves with a constant acceleration of 2ms−2 for half a minute. The brakes are then applied and the train comes to rest in one minute.find (i) the maximum speed attained by the train (ii) the total distance moves by the train and (ii) the positions (s) of the train a half the maximum speed.
View SolutionA train starting from rest moves with a uniform acceleration of 0.2m/s2 for 5 minutes . Calculate the speed acquired and the distance travelled in this time.
View Solution
Knowledge Check
A train starts from rest at S=0 and is subjected to an acceleration as shown in figure. Then,
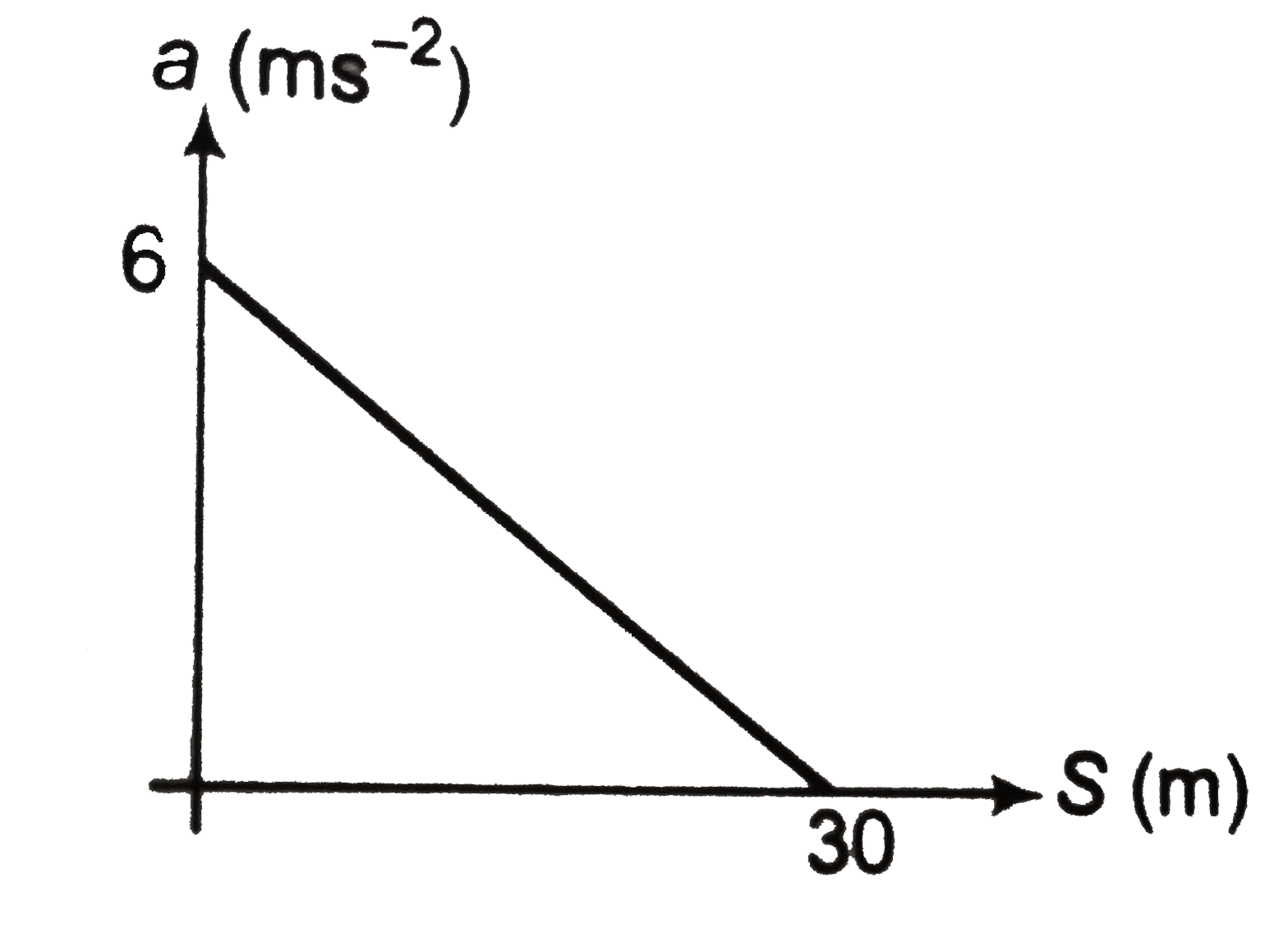 Avelocity at the end of 10 m displacement is 20ms−1Bvelocity of the train at S=10m is 10ms−1CThe maximum velocity attained by train is √180ms−1DThe maximum velocity attained by the train is 15 ms^-1
Avelocity at the end of 10 m displacement is 20ms−1Bvelocity of the train at S=10m is 10ms−1CThe maximum velocity attained by train is √180ms−1DThe maximum velocity attained by the train is 15 ms^-1A train starts from rest with constant acceleration a=1m/s2 A passenger at a distance S from the train runs at this maximum velocity of 10m/s to catch the train at the same moment at which the train starts.
Find the speed of the train when the passenger catches it for the critical distance:A8m/sB10m/sC12m/sD15m/sA train starts from rest and for the first kilometer moveswith constant acceleration. For the next 3 kilometers it has constant velocity and for another two kilometers it moves with constant retardation to come to rest after a total time of 10 minutes. The maximum velocity of the train is
A18 km/hB36 km/hC54 km/hD39 km/h
A train starts from a station and moves with a constant acceleration for 2 minutes. If it covers a distance of 400m in this period, find the acceleration.
View SolutionA train starting from rest moves with a uniform acceleration of 0.2m/s2 for 5 minutes . Calculate the speed acquired and the distance travelled in this time.
View SolutionA particle starts from rest and moves with a constant acceleration of 4m/s2 for 10s, then it moves under constant seceleration and stops in 20s. Find (a) the maximum velocity attained by the particle (b) the total distance traveled and (c ) the distance/distances from the origin, when the particle is moving at half the maximum velocity.
View SolutionA train starts from rest and accelerates uniformly at a rate of 2ms−2 for 10 s. It then maintains a constant speed for 200 s. The brakes are then applied and the train is uniformly retarded and it comes to rest in 50 s. Find
(i) the maximum velocity reached,
(ii) the retardation in the last 50 s,
(iii) the total distance travelled, and
(iv) the average velocity of the train.
View SolutionA train starts from rest with constant acceleration a=1m/s2 A passenger at a distance S from the train runs at this maximum velocity of 10m/s to catch the train at the same moment at which the train starts.
Find the critical distance Sc for which passenger will take the ten seconds time to catch the train
View Solution
