A transverse mechanical harmonic wave is travellling on a string. Maximum velocity and maximum acceleration of a particle on the string are 3m/s and 90m/s2, respectively. If the wave is travelling with a speed of 20m/s on the string, write wave function describing the wave. \
To write the wave function for the given transverse mechanical harmonic wave traveling on a string, we can follow these steps:
Step 1: Identify Given Values
We are given:
- Maximum velocity, Vm=3m/s
- Maximum acceleration, Am=90m/s2
- Wave speed, v=20m/s
Step 2: Write the General Wave Function
The general equation of a sinusoidal wave can be expressed as:
y(x,t)=Asin(ωt±kx)
where:
- A is the amplitude,
- ω is the angular frequency,
- k is the wave number.
Step 3: Relate Maximum Velocity and Maximum Acceleration to Amplitude and Angular Frequency
The maximum velocity Vm and maximum acceleration Am can be expressed in terms of amplitude A and angular frequency ω:
1. Vm=Aω (Equation 1)
2. Am=Aω2 (Equation 2)
Step 4: Solve for Angular Frequency
From Equation 1, we can express ω:
ω=VmA
From Equation 2, we can express A:
A=Amω2
Step 5: Divide Equation 2 by Equation 1
Dividing Equation 2 by Equation 1 gives:
AmVm=Aω2Aω⟹AmVm=ω
Substituting the known values:
ω=90m/s23m/s=30rad/s
Step 6: Find Amplitude
Now, substituting ω back into Equation 1 to find A:
3=A⋅30⟹A=330=0.1m
Step 7: Find Wave Number k
The wave speed v is related to ω and k by:
v=ωk⟹k=ωv
Substituting the known values:
k=30rad/s20m/s=1.5m−1
Step 8: Write the Wave Function
Now we can write the wave function:
y(x,t)=0.1sin(30t±1.5x)
The sign depends on the direction of wave propagation. If the wave is traveling in the positive x-direction, we use the negative sign:
y(x,t)=0.1sin(30t−1.5x)
Final Answer
The wave function describing the wave is:
y(x,t)=0.1sin(30t−1.5x)
We are given:
- Maximum velocity, Vm=3m/s
- Maximum acceleration, Am=90m/s2
- Wave speed, v=20m/s
The general equation of a sinusoidal wave can be expressed as:
y(x,t)=Asin(ωt±kx)
where:
- A is the amplitude,
- ω is the angular frequency,
- k is the wave number.
The maximum velocity Vm and maximum acceleration Am can be expressed in terms of amplitude A and angular frequency ω:
1. Vm=Aω (Equation 1)
2. Am=Aω2 (Equation 2)
From Equation 1, we can express ω:
ω=VmA
From Equation 2, we can express A:
A=Amω2
Dividing Equation 2 by Equation 1 gives:
AmVm=Aω2Aω⟹AmVm=ω
Substituting the known values:
ω=90m/s23m/s=30rad/s
Now, substituting ω back into Equation 1 to find A:
3=A⋅30⟹A=330=0.1m
The wave speed v is related to ω and k by:
v=ωk⟹k=ωv
Substituting the known values:
k=30rad/s20m/s=1.5m−1
Now we can write the wave function:
y(x,t)=0.1sin(30t±1.5x)
The sign depends on the direction of wave propagation. If the wave is traveling in the positive x-direction, we use the negative sign:
y(x,t)=0.1sin(30t−1.5x)
The wave function describing the wave is:
y(x,t)=0.1sin(30t−1.5x)
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRAVELLING WAVESEXERCISE - Exercise 5.19videos
TRAVELLING WAVES
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRAVELLING WAVESEXERCISE - Exercise 5.223videos
TRAVELLING WAVES
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRAVELLING WAVESEXERCISE - Integer9videos
TRAVELLING WAVES
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRANSMISSION OF HEATEXERCISE - Single correct9videos
TRANSMISSION OF HEAT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct5videos
VECTORS
Similar Questions
Knowledge Check
- Question 1 - Select One
The speed of transverse wave on a stretched string is
Adirectly proportional to the tension in the stringBdirectly proportional to the square root of the tensionCinversely proportional to liveDinversely proportional to sqyare of tension
The maximum transverse velocity and maximum transverse acceleration of a harmonic wave in a one - dimensional string are 1ms−1and1ms−2 respectively. The phase velocity of the wave is 1ms−1. The waveform is
View SolutionA transverse wave travelling in a string produce maximum transverse velocity of 3m/s and maximum transverse acceleration 90m/s2 in a particle. If the velocity of wave in the string is 20m/s. Datermine the equation of the wave ?
View SolutionA harmonic wave is travelling along +ve x-axis, on a stretched string. If wavelength of the wave gets doubled, then
View SolutionThe frequency of the wave propagating on a string is 20Hz. What will be the difference in phase of a particle of the string in a time interval of 0.01 s ?
View SolutionA standing wave pattern of maximum amplitude 2 mm is obtained in a string whose shape at t = 0 is represented in the graph.
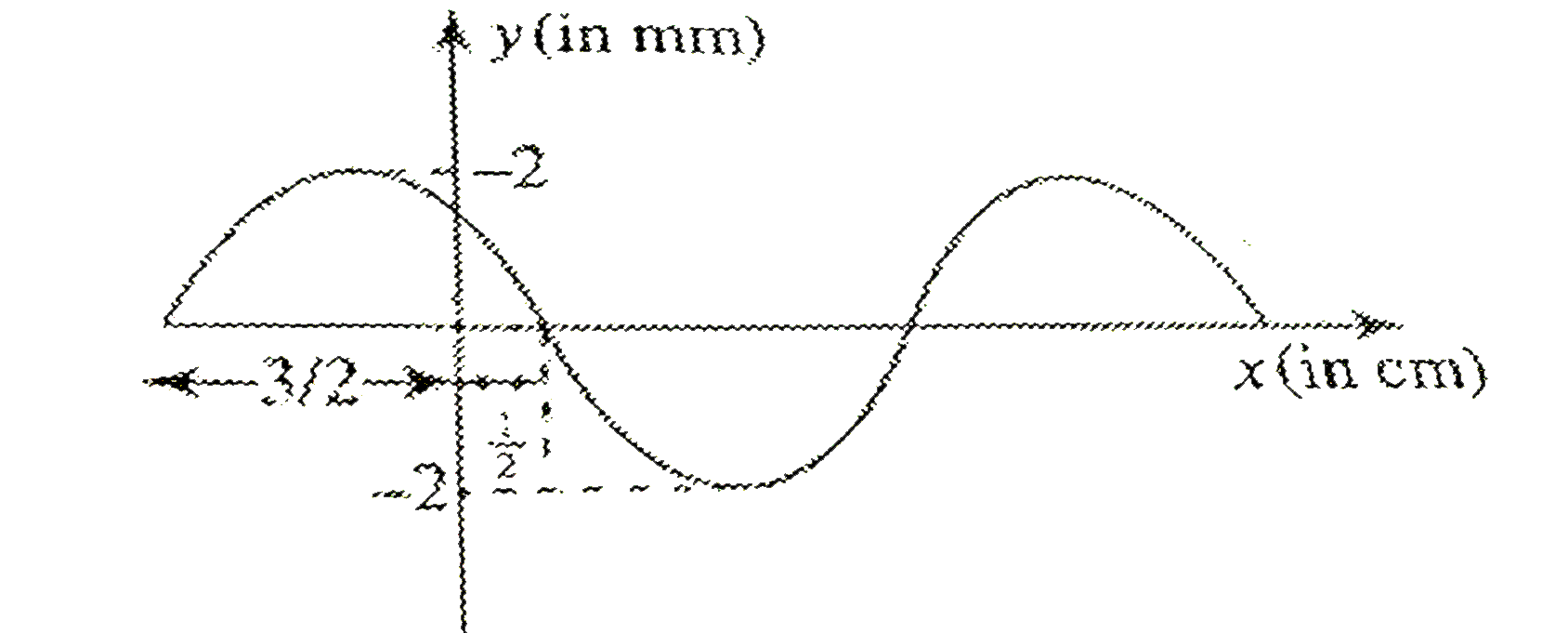
If the speed of the travelling wave in the string is 5 cm/s, then find the component waves.View SolutionA transverse wave is travelling along a string from right to left. The figure represents the shape of the string at the given instant. A point M has a velocity
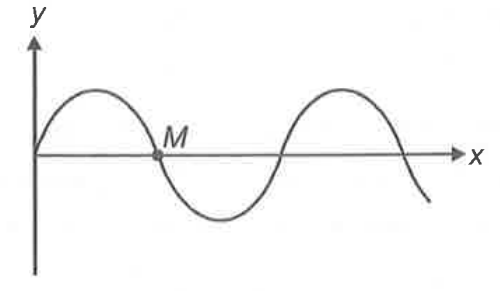 View Solution
View SolutionA string of 7m length has a mass of 0.035kg. If tension in the string is 60.N, then speed of a wave on the string is
View Solution

