A triangular lamina of area A and height h is immersed in a liquid of density ρ in a vertical plane with its base on the surface of the liquid. The thrust on the lamina is.
12Aρgh
13Aρgh
16Aρgh
23Aρgh
The correct Answer is:D
To find the thrust on a triangular lamina immersed in a liquid, we can follow these steps:
1. Understand the Setup:
- We have a triangular lamina with area A and height h immersed in a liquid of density ρ.
- The base of the triangle is on the surface of the liquid.
2. Identify the Pressure at Depth:
- The pressure P at a depth y in the liquid is given by:
P=ρgy
where g is the acceleration due to gravity.
3. Consider a Differential Strip:
- Consider a small horizontal strip of the triangle at depth y with thickness dy and width b.
- The area of this differential strip dA is:
dA=bdy
4. Calculate the Thrust on the Differential Strip:
- The thrust dF on this small strip due to pressure is:
dF=P⋅dA=ρgy⋅bdy
5. Relate Width b to Height y:
- By similarity of triangles, we can express b in terms of y:
yb=hB⟹b=yBh
where B is the base length of the triangle.
6. Substitute b into the Thrust Equation:
- Substitute b into the thrust equation:
dF=ρgy⋅(yBh)dy=ρgBhy2dy
7. Integrate to Find Total Thrust:
- To find the total thrust F, integrate dF from 0 to h:
F=∫h0ρgBhy2dy
- The integral of y2 is:
∫y2dy=y33
- Evaluating the integral from 0 to h:
F=ρgBh⋅(h33−0)=ρgBh23
8. Express in Terms of Area:
- The area A of the triangular lamina is:
A=12Bh
- Rearranging gives B=2Ah.
- Substitute B back into the thrust equation:
F=ρg3⋅(2Ah)h2=23ρgAh
Final Answer:
The thrust on the triangular lamina is:
F=23ρgAh
- We have a triangular lamina with area A and height h immersed in a liquid of density ρ.
- The base of the triangle is on the surface of the liquid.
- The pressure P at a depth y in the liquid is given by:
P=ρgy
where g is the acceleration due to gravity.
- Consider a small horizontal strip of the triangle at depth y with thickness dy and width b.
- The area of this differential strip dA is:
dA=bdy
- The thrust dF on this small strip due to pressure is:
dF=P⋅dA=ρgy⋅bdy
- By similarity of triangles, we can express b in terms of y:
yb=hB⟹b=yBh
where B is the base length of the triangle.
- Substitute b into the thrust equation:
dF=ρgy⋅(yBh)dy=ρgBhy2dy
- To find the total thrust F, integrate dF from 0 to h:
F=∫h0ρgBhy2dy
- The integral of y2 is:
∫y2dy=y33
- Evaluating the integral from 0 to h:
F=ρgBh⋅(h33−0)=ρgBh23
- The area A of the triangular lamina is:
A=12Bh
- Rearranging gives B=2Ah.
- Substitute B back into the thrust equation:
F=ρg3⋅(2Ah)h2=23ρgAh
The thrust on the triangular lamina is:
F=23ρgAh
Topper's Solved these Questions
Similar Questions
Triangular Lamina About Its Base
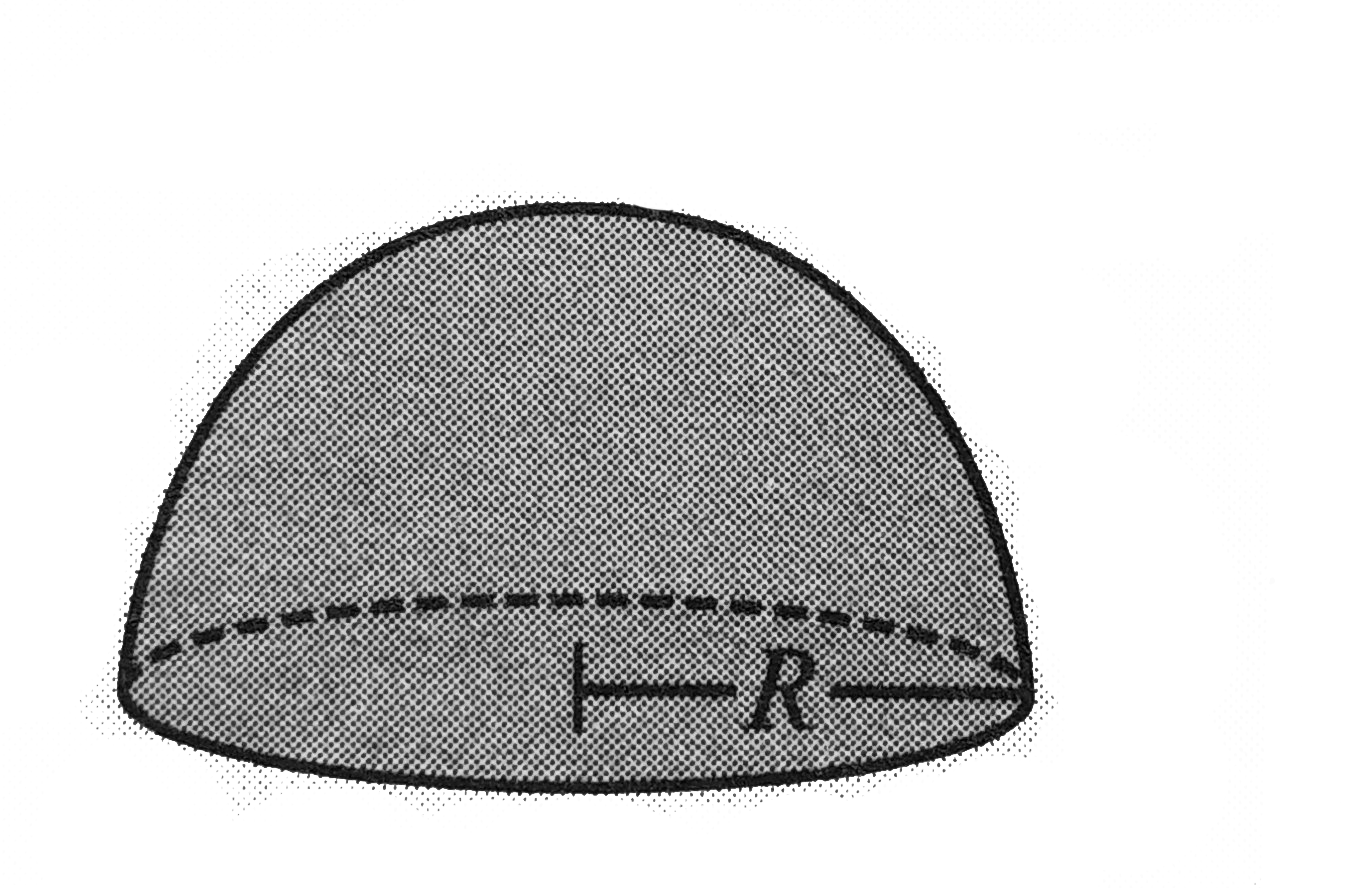
View SolutionA solid hemisphere of radius R is made to just sink in a liquid of density ρ. Find a. the vertical thrust on the curved surface b. the vertical thrust on the flat surface c. the side thrust on the hemisphere. d. the total hydrostatic force acting on the hemisphere.
View Solution
Knowledge Check
A cylindrical block of the density ρ is partically immersed in a liwuid of density 3ρ. The plane surface of the block remains parallel to the surface of the liquid. The height of the block is 60m. The block perform SHM when displaced form its mean position [Use g=9.8m/s2]
Athe maximum amplitude is 20cm.Bthe maximum amplitude is 40cmCthe time period will be 2π/7 secondsDnoneA ball of mass m and density ρ is immersed in a liquid of density 3ρ at a depth h and released. To what height will the ball jump up above the surface of liqud ? (neglect the reistance of water and air).
AhBh/2C2hD3hA small ball of density ρ is immersed in a liquid of density σ(>ρ) to a depth h and released. The height above the surface of water up to which the ball will jump is
A(σρ−1)hB(ρσ−1)hC(ρσ+1)hD(σρ+1)h
A drop of liquid of density ρ is floating half-immersed in a liquid of density d. If ρ is the surface tension the diameter of the drop of the liquid is
View SolutionA drop of liquid of density ρ is floating half-immersed in a liquid of density d. If ρ is the surface tension the diameter of the drop of the liquid is
View SolutionAn isosceles triangular plates of base 3 m and altitude 3 m is immersed in oil vertically with its base coinciding with its base coinciding with the free surface of the oil of relative density 0.8. Determine the total thrust.
View SolutionA body of volume V and density d is completely immersed in a liquid of density p. Then the apparent weight of the body will be:
View SolutionA uniformly tapering vessel of height h whose lower and upper radii are r and R is completely filled with a liquid of density ρ The force that acts on the base of the vessel due of the liquid is
View Solution
