A turn of radius is banked for the vehicle of mass going at a speed of . Find the direction and magnitude of frictional force
(a)
(b)
Assume that friction is sufficient to prevent slipping.
To solve the problem of finding the direction and magnitude of the frictional force acting on a vehicle of mass 200 kg going around a banked turn of radius 20 m at two different speeds (5 m/s and 15 m/s), we will follow these steps:
Step 1: Determine the banking angle (θ) at the speed of 10 m/s
The banking angle can be calculated using the formula:
tanθ=v2rg
Where:
- v=10m/s (speed of the vehicle)
- r=20m (radius of the turn)
- g=10m/s2 (acceleration due to gravity)
Substituting the values:
tanθ=10220×10=100200=12
Thus,
θ=tan−1(12)≈26.57∘
Step 2: Analyze the case for v=5m/s
Since the speed is less than 10 m/s, the vehicle tends to slide down the bank. The frictional force will act up the slope.
1. Forces in the x-direction:
Nsinθ−F=mv2r
(where F is the frictional force)
2. Forces in the y-direction:
Ncosθ=mg+Fsinθ
Step 3: Solve for the normal force (N)
From the y-direction equation:
N=mg+Fsinθcosθ
Step 4: Substitute N into the x-direction equation
Substituting N into the x-direction equation:
(mg+Fsinθcosθ)sinθ−F=mv2r
Step 5: Substitute known values for v=5m/s
Substituting m=200kg, r=20m, g=10m/s2, and θ≈26.57∘:
200×10+Fsin(26.57∘)cos(26.57∘)sin(26.57∘)−F=200×5220
Calculating the right-hand side:
200×2520=250
Step 6: Solve for F
After substituting and simplifying, we can find the value of F.
Step 7: Analyze the case for v=15m/s
In this case, since the speed is greater than 10 m/s, the vehicle tends to slide up the bank. The frictional force will act down the slope.
1. Forces in the x-direction:
Nsinθ+F=mv2r
2. Forces in the y-direction:
Ncosθ=mg−Fsinθ
Step 8: Solve for the normal force (N) again
From the y-direction equation:
N=mg−Fsinθcosθ
Step 9: Substitute N into the x-direction equation
Substituting N into the x-direction equation:
(mg−Fsinθcosθ)sinθ+F=mv2r
Step 10: Substitute known values for v=15m/s
Substituting m=200kg, r=20m, g=10m/s2, and θ≈26.57∘:
200×10−Fsin(26.57∘)cos(26.57∘)sin(26.57∘)+F=200×15220
Calculating the right-hand side:
200×22520=2250
Step 11: Solve for F
After substituting and simplifying, we can find the value of F.
Final Answers
- For v=5m/s: F≈300√5N (up the slope)
- For v=15m/s: F≈500√5N (down the slope)
tanθ=v2rg
Where:
- v=10m/s (speed of the vehicle)
- r=20m (radius of the turn)
- g=10m/s2 (acceleration due to gravity)
tanθ=10220×10=100200=12
Thus,
θ=tan−1(12)≈26.57∘
Nsinθ−F=mv2r
(where F is the frictional force)
Ncosθ=mg+Fsinθ
N=mg+Fsinθcosθ
(mg+Fsinθcosθ)sinθ−F=mv2r
200×10+Fsin(26.57∘)cos(26.57∘)sin(26.57∘)−F=200×5220
200×2520=250
Nsinθ+F=mv2r
Ncosθ=mg−Fsinθ
N=mg−Fsinθcosθ
(mg−Fsinθcosθ)sinθ+F=mv2r
200×10−Fsin(26.57∘)cos(26.57∘)sin(26.57∘)+F=200×15220
200×22520=2250
- For v=5m/s: F≈300√5N (up the slope)
- For v=15m/s: F≈500√5N (down the slope)
Topper's Solved these Questions
- CIRCULAR MOTIONBook:DC PANDEY ENGLISHChapter:CIRCULAR MOTIONExercise:Solved Examples
Explore 2 Videos
- CIRCULAR MOTIONBook:DC PANDEY ENGLISHChapter:CIRCULAR MOTIONExercise:Miscellaneous Examples
Explore 5 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBook:DC PANDEY ENGLISHChapter:CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONExercise:Level 2 Subjective
Explore 21 Videos
- COMMUNICATION SYSTEMBook:DC PANDEY ENGLISHChapter:COMMUNICATION SYSTEMExercise:Only One Option is Correct
Explore 27 Videos
Similar Questions
A turn of radius 600 m is banked for a vehicle of mass 200 kg going with a speed of 180kmh−1 . Determine the banking angle of its path.
View SolutionA man travels 200 km distance with the speed of 40 m/s and next 50 km with the speed of 10 m/s . Find the average speed of man.
View SolutionA block of mass 2.00 kg moving at a speed of 10.0 m/s accelerates at 3.0 ms2 for 5.00 s. Compute its final kinetic enegy.
View SolutionA body of mass 5 kg is taken a height 5 m to 10 m .Find the increase in its potential energy (g=10 m s−2)
View SolutionA ball of mass 0⋅2 kg moving with a speed of 30 m/s strikes a bat returns in opposite direction with speed of 90m/s . Magnitude of change in momentu,m of ball will be
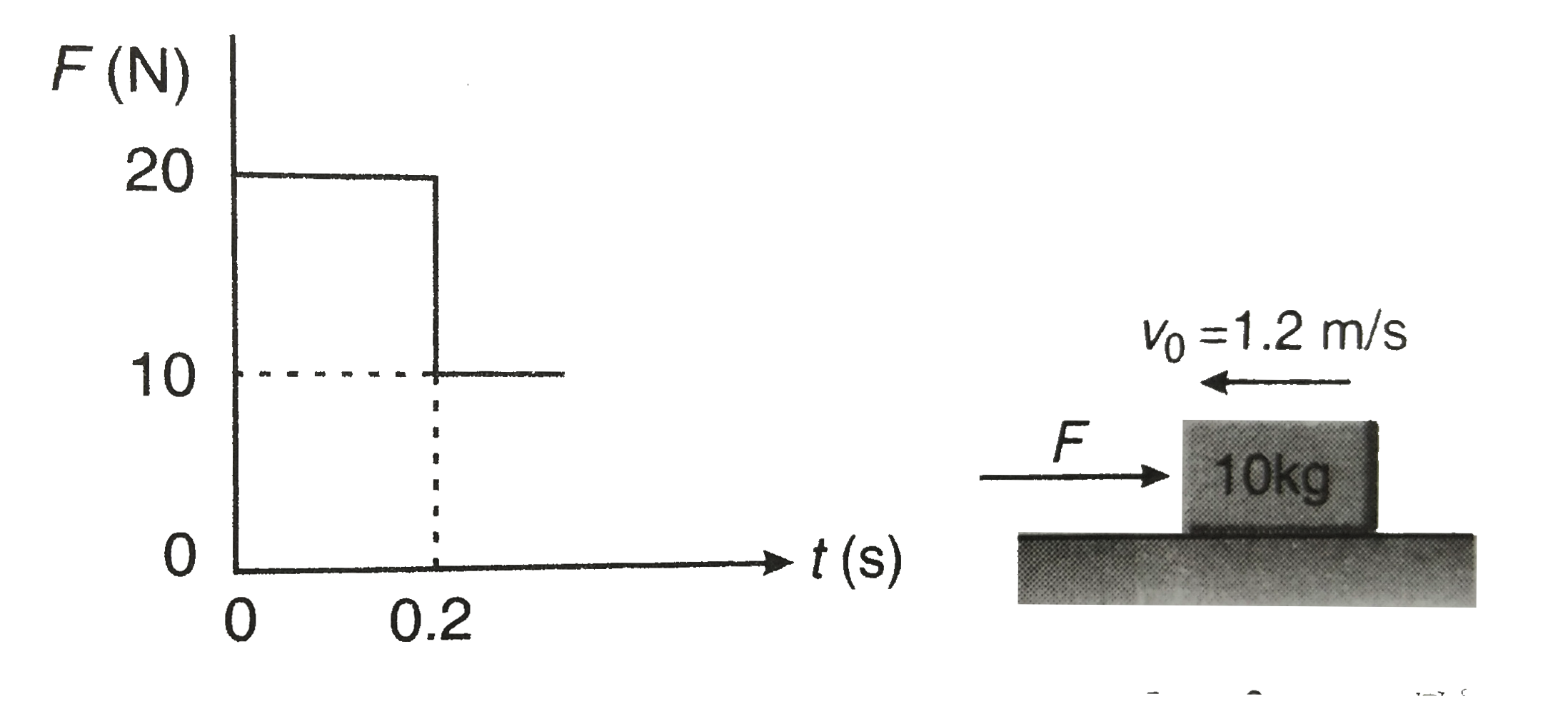
View SolutionThe 10kg block is moving to the left with a speed of 1.2m/s at time t=0 A force F is applied kinetic friction is μk=0.2. Determine the time t at which the block comes to a slip. (g=10m/s2)
View SolutionA body of mass 10 kg moving at a height of 2 m, with uniform speed of 2 m/s. Its total energy is
View SolutionA marble block of mass 2 kg lying on ice when given a velocity of 6m/s is stopped by friction in 10s. Then the coefficient of friction is
View SolutionA marble block of mass 2 kg lying on ice when given a velocity of 6m/s is stopped by friction in 10s. Then the coefficient of friction is
View SolutionA block of mass 20 kg is on a horizontal plane of a coefficient of friction 0.5. by applying 6.0 newton force on it, frictional force will be (g=10m/s2).
View Solution
